Mi van, ha az adataink NEM normálisak?

Bevezetés

Itt a Halloween-hét, és a trükkök és a finomságok között mi, adatgeekek, a közösségi médiában ezen a cuki mémeken kuncogunk.

Azt hiszed, hogy ez egy vicc? Hadd mondjam el neked, hogy ez nem nevetséges. Ez ijesztő, hűen a Halloween szelleméhez!

Ha nem tudjuk feltételezni, hogy a legtöbb (üzleti, társadalmi, gazdasági vagy tudományos eredetű) adatunk legalább megközelítőleg “normális” (azaz egy Gauss-folyamat vagy több ilyen folyamat összege által generált), akkor végünk van!

Itt egy rendkívül rövid lista azokról a dolgokról, amelyek nem lesznek érvényesek,

• A hat-szigma egész fogalma
• A híres 68-95-99,7 szabály
• A p=0,05 (2 szigma intervallumból származik) “szent” fogalma a statisztikai elemzésben

Elég ijesztő? Beszéljünk róla bővebben…

A mindenható és mindenütt jelenlévő normális eloszlás

Legyen ez a rész rövid és tömör.

A normális (Gauss) eloszlás a legismertebb valószínűségi eloszlás. Íme néhány link a hatalmát és széleskörű alkalmazhatóságát leíró cikkekhez,

• Miért szeretik az adattudósok a Gauss-t

• How to Dominate the Statistics Portion of Your Data Science Interview
• What’s So Important about the Normal Distribution?

A különböző területeken való megjelenése és a központi határértéktétel (CLT) miatt ez az eloszlás központi helyet foglal el az adattudományban és az analitikában.

Szóval, mi a probléma?

Ez mind szép és jó, mi a probléma?

A probléma az, hogy gyakran előfordulhat, hogy az adott adatkészlethez olyan eloszlást találunk, amely nem felel meg a normalitásnak, azaz a normális eloszlás tulajdonságainak. De a normalitás feltételezésétől való túlzott függés miatt a legtöbb üzleti elemzési keretrendszer a Normális eloszlású adathalmazokkal való munkára van szabva.

Ez szinte beleivódott a tudatalattinkba.

Tegyük fel, hogy arra kérik, hogy észlelje, ellenőrizze, van-e értelme egy új adattételnek valamilyen folyamatból (mérnöki vagy üzleti). A “van értelme” alatt azt érted, hogy az új adatok tartoznak-e, azaz az “elvárt tartományon” belül vannak-e.

Mi ez az “elvárás”? Hogyan számszerűsíthetjük a tartományt?

Automatikusan, mintha egy tudatalatti késztetés irányítaná, megmérjük a mintaadathalmaz átlagát és szórását, és tovább vizsgáljuk, hogy az új adat bizonyos szórástartományba esik-e.

Ha 95%-os konfidenciahatárral kell dolgoznunk, akkor örülünk, ha az adat 2 szóráson belülre esik. Ha szigorúbb korlátra van szükségünk, akkor 3 vagy 4 standard eltérést vizsgálunk. Kiszámítjuk a Cpk-t, vagy a ppm (parts-per-million) minőségi szintre vonatkozó six-sigma irányelveket követjük.

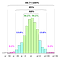
Mindezen számítások azon az implicit feltételezésen alapulnak, hogy a populációs adatok (NEM a minta) Gauss-eloszlást követ i.azaz az alapvető folyamatot, amelyből az összes adat keletkezett (a múltban és a jelenben), a bal oldali minta szabályozza.

De mi történik, ha az adatok a jobb oldali mintát követik?

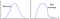
Vagy ez, és… az?

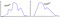
Létezik-e univerzálisabb korlát, ha az adatok NEM normálisak?

A nap végén akkor is szükségünk lesz egy matematikailag megalapozott technikára a bizalmi korlátunk számszerűsítésére, ha az adatok nem normálisak. Ez azt jelenti, hogy a számításunk egy kicsit változhat, de akkor is valami ilyesmit kell tudnunk mondani-

“Annak a valószínűsége, hogy egy új adatpontot az átlagtól egy bizonyos távolságban figyelünk meg, ilyen és ilyen…”

Kézenfekvő, hogy a 68-95-99-es, dédelgetett Gauss-határoknál univerzálisabb határt kell keresnünk.7 (ami az átlagtól való 1/2/3 standard eltérésnyi távolságnak felel meg).

Szerencsére létezik egy ilyen korlát, az úgynevezett “Chebyshev-határ”.

Mi a Chebyshev-határ és hogyan hasznos?

A Chebyshev-egyenlőtlenség (más néven Bienaymé-Chebyshev-egyenlőtlenség) garantálja, hogy a valószínűségi eloszlások egy széles osztálya esetében az értékeknek legfeljebb egy bizonyos töredéke lehet az átlagtól egy bizonyos távolságnál nagyobb.

Pontosabban, az eloszlás értékeinek legfeljebb 1/k² része lehet k standard eltérésnél nagyobb távolságra az átlagtól (vagy ennek megfelelően az eloszlás értékeinek legalább 1-1/k² része k standard eltérésen belül van az átlagtól).

Ez gyakorlatilag korlátlan számú valószínűségi eloszlástípusra alkalmazható, és sokkal lazább feltételezéssel működik, mint a normalitás.

Hogyan működik?

Még ha nem is tudsz semmit az adataid mögötti titkos folyamatról, jó eséllyel mondhatod a következőket,

“Biztos vagyok benne, hogy az adatok 75%-ának 2 szóráson belül kell lennie az átlagtól”,

vagy,

biztos vagyok benne, hogy az adatok 89%-ának 3 szóráson belül kell lennie az átlagtól”.

Íme, így néz ki ez egy tetszőlegesen kinéző eloszlás esetén,

Hogyan kell alkalmazni?

Amint mostanra már sejtheted, az adatelemzés alapvető mechanikájának cseppet sem kell változnia. Továbbra is gyűjteni fogsz egy mintát az adatokból (minél nagyobbat, annál jobb), kiszámítod ugyanazt a két mennyiséget, amit megszoktál – az átlagot és a szórást -, majd a 68-95-99,7 szabály helyett az új korlátokat alkalmazod.

A táblázat a következőképpen néz ki (itt k azt jelöli, hogy hány szórásnyira van az átlagtól),

Az alkalmazásáról szóló videós bemutató itt,

Mi a bökkenő? Miért nem használják az emberek ezt az “univerzálisabb” kötést?

A táblázatra vagy a matematikai definícióra pillantva nyilvánvaló, hogy mi a bökkenő. A Chebyshev-szabály sokkal gyengébb, mint a Gauss-szabály az adatokra vonatkozó korlátok felállításának kérdésében.

Egy 1/k²-es mintázatot követ, szemben a Normál-eloszlás exponenciálisan csökkenő mintázatával.

Például, ha 95%-os megbízhatósággal akarunk bármit is korlátozni, akkor 4,5 standard eltérésig kell adatokat bevonni vs. csak 2 standard eltérést (a Normál eloszláshoz).

De még mindig megmentheti a helyzetet, ha az adatok egyáltalán nem hasonlítanak a Normál eloszlásra.

Van valami jobb?

Van egy másik korlát, a “Chernoff-kötés”/Hoeffding egyenlőtlenség, amely exponenciálisan éles eloszlást ad (az 1/k²-hez képest) független véletlen változók összegére.

Ezt is használhatjuk a Gauss-eloszlás helyett, ha az adatok nem tűnnek Normálisnak, de csak akkor, ha nagyfokú bizalmunk van abban, hogy a mögöttes folyamat egymástól teljesen független részfolyamatokból áll.

Szerencsétlenségünkre sok társadalmi és üzleti esetben a végső adat sok alfolyamat rendkívül bonyolult kölcsönhatásának eredménye, amelyek között erős kölcsönös függőség állhat fenn.”

Összefoglaló

Ebben a cikkben megismertünk egy sajátos típusú statisztikai korlátot, amely a normalitás feltételezésétől függetlenül a lehető legszélesebb eloszlású adatokra alkalmazható. Ez akkor jön jól, ha nagyon keveset tudunk az adatok valódi forrásáról, és nem feltételezhetjük, hogy azok Gauss-eloszlást követnek. A korlát az exponenciális jelleg helyett (mint a Gaussé) hatványtörvényt követ, és ezért gyengébb. De fontos eszköz a repertoárjában bármilyen tetszőleges típusú adateloszlás elemzéséhez.