Miért egyenlő 0,999…1?!

Az összegzésünkben szereplő tagokról úgy is gondolkodhatunk, hogy minden egyes egymást követő tagot úgy kapunk, hogy az előzőt megszorozzuk egy közös aránnyal.

Ez azt jelenti, hogy van egy geometriai sorozatunk, amely a/(1 – r) értékhez konvergál, ahol a a az első érték a sorozatban, és r az az arány, amellyel megszorozzuk a következő tagot.

A sorozat konvergenciája egyszerűen azt jelenti, hogy a sorozat egyre közelebb és közelebb kerül egy adott értékhez, ahogy egyre több és több tagot adunk a sorozathoz. A sorozat végtelenül közelít a konvergenciaértékhez. Végtelen skálán a konvergencia egyenlőséggé válik.

A mi esetünkben 1/10-ről indulunk, és minden alkalommal 1/10-zel szorzunk, tehát mind a, mind r = 1/10.

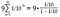
Végezzük el az aritmetikát a jobb oldalon.

Most formálisan megmutattuk, hogy 0.999…. konvergál vagy egyenlő 1-gyel.

Végső gondolatok & Inspiráció

Ha ez furcsának tűnik neked, az jó! Tudod, hogy két különböző szám, valójában különböző számnak kellene lennie. Ennek a problémának a kontraintuitív jellege a végtelennel való munkával járó furcsaság velejárója.

Még egy ilyen egyszerű problémánál is, mint ez, az emberi agy számára kézzelfogható dolgok határaiból egy olyan léptékre lépsz, ami bizonyos értelemben meghaladja a felfogóképességünket. Véges lényekként megragadhatjuk a végtelenség vagy az örökkévalóság fogalmának megértését, de soha nem tapasztalhatjuk meg igazán. Ami azt jelenti, hogy gyakran előfordul, hogy amiről véges világunkban tudjuk, hogy igaz, kiderül, hogy a végtelen szintjén másképp viselkedik.

A matematika szépségének és csodájának része, hogy elfogadjuk az átmenetet a könnyen felfedezhető és reprodukálható matematikától a csak az elménkben tesztelhető és elképzelhető felé.

A mai leckét tehát ne vegyük készpénznek és ne vonjuk meg a vállunkat.

Legyen egy ködréteg köztünk és a tökéletes megértés között. Hagyd, hogy elborítsa az elmédet az a tény, hogy a végtelen furcsán viselkedik. És hagyja, hogy ez még több megértés és legfőképpen még több matematika után vágyakozzon.

Köszönöm, hogy ma elolvasták és velem együtt elmélkedtek a végtelenről!