Funkciók vagy leképezés

A függvényekben vagy leképezésben most a függvényeknek vagy leképezésnek nevezett relációk speciális fajtáját fogjuk tanulmányozni. Ezek megértéséhez vegyünk néhány valós példát.

Mindezekre a kérdésekre
egyedi válaszok adhatók. Nézzük
meg, hogyan tudjuk
összekapcsolni
ezeket a tanulási térképezésben.

● Honnan kel fel a nap?

Kelet

● Melyik India fővárosa?

Delhi

● Mi a 4 utódja?

5

● Mi az 5 és a 3 összege?

8

Térképezés vagy függvények:

Ha A és B két nem üres halmaz, akkor az A halmazból B halmazba való ‘f’ relációt függvénynek vagy leképezésnek mondjuk,
● ha az A halmaz minden eleméhez a B halmaz egyetlen eleme tartozik.

● Az ‘f’ függvényt A-ból B-be f : A → B-vel jelöljük.

●● Ha f egy függvény A-tól B-be és x ∈ A, akkor f(x) ∈ B, ahol f(x) az x f alatti képének, x pedig az f(x) ‘f’ alatti előképének nevezzük.

Megjegyzés:

Hogy f leképezés legyen A-ből B-be:

● A minden elemének kell, hogy legyen képe B-ben. A mellékelt ábra nem jelent leképezést, mivel az A halmaz d eleme nem tartozik a B halmaz egyetlen eleméhez sem.

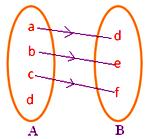
● Az A egyetlen elemének sem lehet egynél több képe. A mellékelt ábra nem ábrázol leképezést, mivel az A halmaz b eleme a B halmaz két d, f eleméhez tartozik.

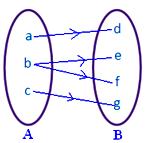
● Az A halmaz különböző elemeinek lehet ugyanaz a képe a B halmazban. A mellékelt ábra egy leképezést ábrázol.

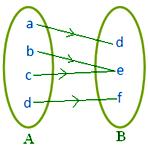
Megjegyzés:

Minden leképezés egy reláció, de nem minden reláció lehet leképezés.

A függvény mint a reláció egy speciális fajtája:

Idézzük fel és tekintsük át a függvényt mint a reláció egy speciális fajtáját Tegyük fel, hogy A és B két nem üres halmaz, akkor egy ‘f’ szabályt, amely A minden egyes elemét B egy egyedi eleméhez társítja, függvénynek vagy A és B közötti leképezésnek nevezzük.
Ha ‘f’ egy leképezés A-tól B-re,

azt úgy fejezzük ki, hogy f: A → B

az ‘f’ egy függvény A-tól B-re.
Ha ‘f ‘ egy függvény A-tól B-re és x∈A és y∈B, akkor azt mondjuk, hogy y az x elem képe az ‘ f ‘ függvény alatt, és f(x) jelöljük.
Ezért írjuk úgy, hogy y = f(x)

Itt az x elemet y előképének nevezzük.

Egy A-tól B-ig tartó függvény esetében tehát
● A és B ne legyen üres.

●● Az ‘A’ minden elemének legyen képe a ‘B’-ben.

● Az ‘A’ egyetlen elemének se legyen egynél több képe a ‘B’-ben.
Megjegyzés:

● “A” két vagy több elemének lehet ugyanaz a képe “B”-ben.

● f : x → y azt jelenti, hogy az “f” A-tól B-ig tartó függvénye alatt “A” x elemének van y képe “B”-ben.

● Minden f képének B-ben kell lennie, de lehetnek olyan elemek “B”-ben, amelyek nem f képei “A” egyetlen elemének sem.

● Relációk és leképezések

Rendezett pár

Két halmaz kartéziánus szorzata

Reláció

Reláció tartománya és tartománya

Függvények vagy leképezések

Tartomány Ko.A függvény tartománya és tartománya

● Relációk és leképezés – Munkalapok

Munkalap a matematikai relációról

Munkalap a függvényekről vagy leképezésről

7. osztályos matematikai feladatok

8. osztályos matematikai gyakorlat
Funkciókból vagy leképezésből a HOME PAGE