Adatszerkezetek:

Miért stackek és sorok?

A tömbökkel ellentétben a stackekben és sorokban nincs véletlenszerű hozzáférési művelet (nem tudunk egy elemhez közvetlenül hozzáférni egy ‘index’ segítségével). Általában kevesebb metódusunk/műveletünk van, amelyeken elvégezhetjük, mint például a push(), pop(), peek(), enqueue(), dequeue(), amelyek mind kizárólag az adatstruktúra elején vagy végén lévő elemmel foglalkoznak.

De…

Kérdés: Ez nagyon korlátozóan hangzik, hiszen az adatszerkezetben csak az első vagy az utolsó elemhez férhetünk hozzá. Miért akarunk egyáltalán ilyesmit használni? Miért nem használunk egyszerűen tömböket a nagyobb rugalmasság érdekében?

Válasz:

Válasz: Miért nem használunk egyszerűen tömböket a nagyobb rugalmasság érdekében? A veremek és a sorok általában “magasabb szintű adatszerkezetek”, amelyeket alacsonyabb szintűek (tömb vagy összekapcsolt lista) tetejére építenek, hogy korlátozzák a rajtuk végezhető műveleteket. Ez akkor előnyös, ha korlátozott hozzáférést akarunk.

Ez a korlátozott képesség egy adatstruktúrán előnyös, mert ellenőrizhetjük, hogy ki használja ezt az adatstruktúrát, amely csak a megfelelő, hatékony műveleteket hajtja végre. Nem kell például azon csodálkoznunk, ha valaki véletlenszerűen beilleszt egy elemet a listánk közepére, elrontva ezzel néhány invarianciát. Ez sok problémától mentett meg minket. Nézzük meg őket közelebbről.

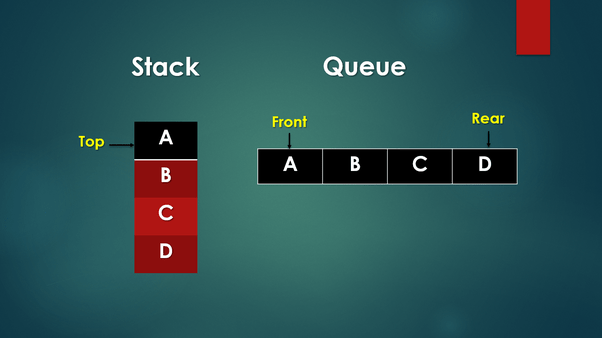
Mi az a verem?

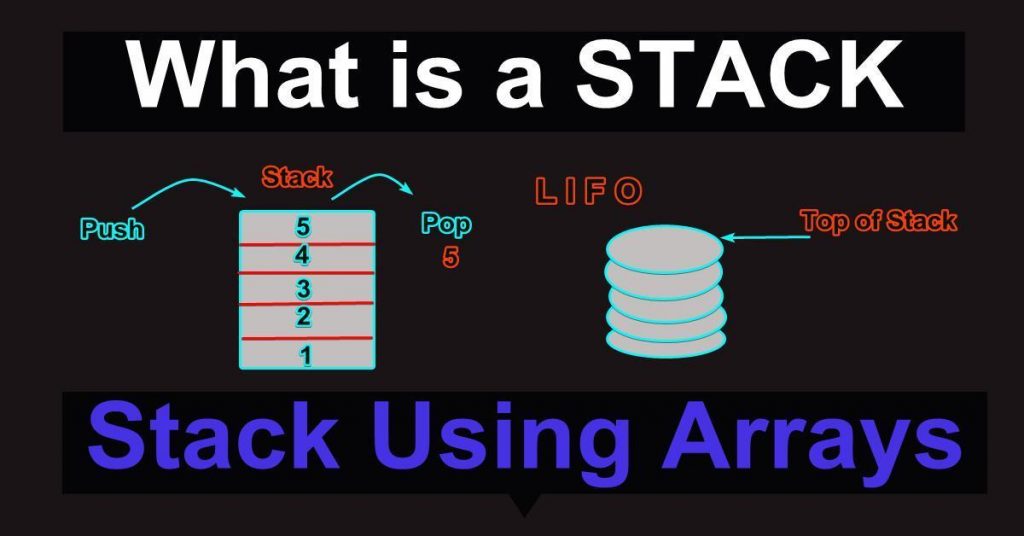
A verem egy egyvégű lineáris adatszerkezet, amely egy valós vermet modellez azzal, hogy két elsődleges művelettel rendelkezik, nevezetesen a push és a pop művelettel.

Az alábbi képen láthatjuk, hogy egy adattagot kivesznek a verem tetejéről, egy másikat pedig hozzáadnak. Van egy felső mutató, amely a verem tetején lévő blokkra mutat. Ez azért van, mert a verem elemei mindig a verem tetejéről kerülnek eltávolításra és a verem tetejére. Ezt a viselkedést általában LIFO (Last In First Out) néven ismerik.

Pakliműveletek

A következő 2 alapvető művelet a veremmel végezhető.

• Push funkció: Egy elem hozzáadása a verem tetejére
• Pop funkció: A legfelső elem eltávolítása (és esetleg visszaadása)

A verem alapműveleteinek szemléltetése

A verem állapotának ellenőrzésére a következő további függvények állnak rendelkezésre.

• Peek függvény: Visszaadja a verem legfelső elemét anélkül, hogy azt eltávolítaná vagy törölné
• isEmpty függvény: Annak ellenőrzése, hogy a verem üres-e vagy sem
• isFull függvény: Annak ellenőrzése, hogy a verem tele van-e vagy sem

Minden a verem tetején működik. Semmi máshoz nem férünk hozzá, csak a tetejéhez. Ez döntő fontosságú a működés megértéséhez.

Bonyolultsági elemzés

Az alábbi bonyolultsági táblázat feltételezi, hogy a veremet összekapcsolt listával valósítottuk meg

Paklik alkalmazásai

Mikor és hol használják a vermet? A programozásban sokszor használjuk a Stack-et anélkül, hogy észrevennénk, íme néhány példa:

• Kifejezések kiértékelésére használható (pl.: egy shunting-yard algoritmus matematikai kifejezések elemzésére és kiértékelésére).
• A rekurziós programozásban függvényhívások megvalósítására használható.

• Szövegszerkesztőkben a visszavonási mechanizmusok segítségével az általunk írt szöveg visszavonására használható (Cmd + Z Mac OS-en és Ctrl + Z Windows-on)
• Böngészőben a visszafelé navigálásra és előre
• Mélységi első keresést (DFS) végezhetünk egy gráfban
• A színfalak mögött a rekurzió támogatására használjuk az előző függvényhívások nyomon követésével

Mi az a Queue?

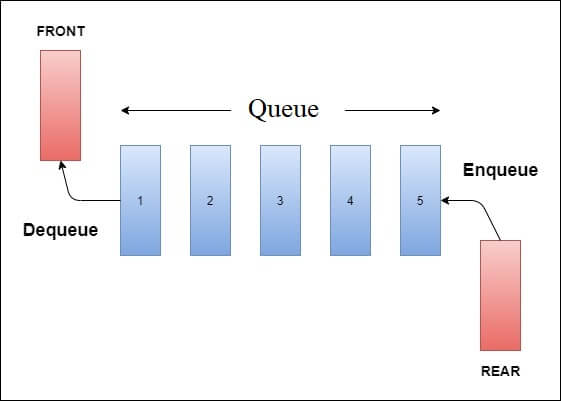
A várólista szintén egy lineáris adatszerkezet, amely a valós világbeli várólistákat modellezi azáltal, hogy két elsődleges művelettel rendelkezik, nevezetesen az enqueue (úgy is gondolhatunk rá, mint “belép a várólistába”) és a dequeue (úgy is gondolhatunk rá, mint “törlés a várólistából”). Ezt a struktúrát azért neveztük el “queue”-nak, mert hasonlít egy valós sorra – (ahol emberek várakoznak egy sorban).

Minden sornak van egy elülső és egy hátsó vége (néha “hátsónak” is nevezik). A hátsó végén keresztül helyezünk be elemeket, és az első végén keresztül távolítjuk el őket.

A sorban állás egy FIFO (First In First Out – az első helyen elhelyezett elemhez lehet először hozzáférni) struktúra, amely gyakran megtalálható számos programozási nyelvben.

Várólista műveletek

A következő 3 alapvető műveletet lehet elvégezni egy várólistán.

• Enqueue funkció: Egy elem hozzáadása a várólista végéhez
• Dequeue funkció: Elem eltávolítása a várólista elejéről
• Peeking függvény: A sor elején lévő érték megnézése anélkül, hogy eltávolítanánk

Bonyolultsági elemzés

Amint a képen látható, a sorba állítás és a sorból való eltávolítás műveletei állandó O(1) időt vesznek igénybe. Annak ellenőrzése azonban, hogy egy elem benne van-e a sorban, lineárisan O(n) idejű, mivel potenciálisan az összes elemet végig kellene pásztáznunk.

Elemek eltávolítása (nem a sorból való eltávolítás) is létezik belsőleg. Ez lineáris időt igényel, mivel legrosszabb esetben az összes elemet végig kell pásztáznunk.

Várólistás alkalmazások

• A többszálú szálak kezelésére használjuk.
• Az x legutóbb hozzáadott elem hatékony nyomon követésére használható
• Webszerver kérések kezelése, ahol azt akarjuk, hogy az érkezési sorrendben szolgáljanak ki. Például: Egy adott pillanatban a webszerverünk csak maximum 50 embert tud egyszerre kiszolgálni.

Ha rövid időn belül 70 kérés érkezik, akkor nem tudjuk mindet feldolgozni. Ezért a webkiszolgáló csak 50 kérést emel ki a sorból, a maradék 20-at pedig várakoztatja. Amikor a webkiszolgáló befejezi egy kérés feldolgozását, akkor a következő kiszolgálandó kérést leveszi a sorból, és ezt addig folytatja, amíg a sor ki nem ürül.

• Breadth-first search (BFS) graph traversal
• Sorbanállási rendszerek (pl.: priority queues)
• Hálózati nyomtatókban használatos: A nyomtató egyszerre csak egyetlen kérést tud kiszolgálni. Ha tehát más kérések érkeznek, amikor a nyomtató foglalt, a nyomtatót kezelő program nem utasítja el ezeket a kéréseket, hanem sorba állítja őket, és várakozik a végrehajtásra. Az első kérést szolgálja ki először (FIFO).

Reméljük, hogy ez a cikk képet adott Önnek a halmokról és a várólistákról a fejében. Ne felejtsen el feliratkozni blogunkra, és kövesse a Designveloper Facebook, Twitter és LinkedIn oldalát.

És ezek a további cikkek is érdekelhetik:

• Mi a webes alkalmazásarchitektúra?
• Adatstruktúrák és alkalmazásuk
• Mi a Big O jelölés?