A kör kerülete – Magyarázat és példák

Az előbb láttuk, hogyan határozzuk meg a sokszög kerületét. Tudjuk, hogy a kör nem sokszög, ezért nem lehet kerülete. Egy egyenértékű formát használunk a körre, amit kerületnek nevezünk.

Ebben a cikkben arról lesz szó, hogyan találjuk meg a kör kerületét, a kör kerületének képletét és a kör kerületével kapcsolatos példafeladatokat.

Mi a kör kerülete?

A sokszög, például négyzet vagy téglalap körüli távolságot kerületnek (P) nevezzük. Másrészt a kör körüli távolságot kerületnek (C) nevezzük. A kör kerülete tehát a kör egyik élének lineáris távolsága.

Miért van szükségünk a kör kerületének kiszámítására?

A tárgy kerületének meghatározása a következő esetekben fontos:

Ha melltartót, nadrágot vagy pulóvert szeretne vásárolni, ismernie kell a derék vagy mellkas körüli távolságot. Bár a teste nem tökéletes kör, a kerületét mérőszalaggal kell megmérnie. A szabók többnyire ezt a technikát használják egy ruha kerületének meghatározásához.

A kör kerületét is tudnod kell, ha kézműves munkát végzel, kerítést raksz a pezsgőfürdőd köré, vagy csak megoldasz egy matematikai feladatot az iskolában.

Hogyan találod meg a kör kerületét?

Amint már említettük, a kör kerülete vagy kerülete a kör vagy bármilyen kör alakzat körüli távolság. Egy kör kerülete megegyezik annak az egyenesnek a hosszával, amelyet meghajlítunk vagy meghajlítunk, hogy a kör létrejöjjön. A kör kerületét méterben, kilométerben, yardban, hüvelykben stb. mérik.

A kör kerületének vagy kerületének meghatározására kétféle módszer létezik. Az első képletben a sugarat, a másodikban pedig a kör átmérőjét használjuk. Fontos megjegyezni, hogy mind a két módszer ugyanazt az eredményt adja.

Nézzük meg.

A kör kerülete a következővel adódik;

C = 2 * π* R = 2πR

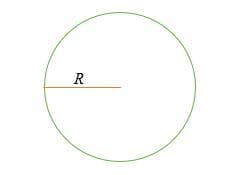
hol,

C = a kör kerület vagy kerület,

R = a kör sugara,

π = a pí néven ismert matematikai állandó

Or

C = π* D = π D

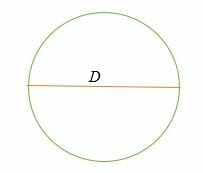
hol,D = 2R = a kör átmérője

Minden kör esetében a kerület és az átmérő hányadosa egyenlő a pí néven ismert állandóval.

Kerület/átmérő = Pi

C /D = Pi vagy C/2R = pi

A pi (π) közelítő értéke = 22/7 = 3,141592926535897….. (nem véges érték)

A kör kerületének könnyebb kiszámítása érdekében a pi értékét 3,14-nek vesszük (π = 3,14).

Lássunk az alábbiakban néhány példát a kerület fogalmának csiszolására.

1. példa

Keresd meg a 8 cm sugarú kör kerületét.

Megoldás

Körfogat = 2 * π* R = 2πR

= 2 * 3,14 * 8

= 50,24 cm.

2. példa

Kalkuláljuk ki egy olyan kör kerületét, amelynek átmérője 70 mm

Megoldás

Kerület = π* D = π D

= 3,14 * 70

= 219.8 mm

3. példa

Kiszámítjuk egy kör alakú virágoskert kerületét, amelynek sugara 10 m.

megoldás

Kerület = 2 * π* R = 2πR

= 2 * 3,14 * 10

= 62,8 m.

4. példa

A kör kerülete 440 méter. Határozzuk meg a kör átmérőjét és sugarát.

Megoldás

Körfogat = 2 * π* R = 2πR

440 =2 * 3,14 * R

440 = 6.28R

Elosztjuk mindkét oldalt 6,28-cal, és megkapjuk,

R = 70,06

Ezért a kör sugara 70,06 yard. De mivel az átmérő a kör sugarának kétszerese, akkor az átmérője 140,12 yard.

5. példa

A kerékpár kerekeinek átmérője 100 cm. Hány fordulatot tesz mindegyik kerék, hogy megtegyen egy 157 méteres távolságot

Megoldás

Kiszámítjuk a kerékpár kerekének kerületét.

Körfogat = π D

= 3.14 * 100

= 314 cm

A kerék fordulatszámának kiszámításához osszuk el a megtett távolságot a kerék kerületével.

Az osztás előtt át kell számolnunk 157 métert cm-re, tehát megszorozzuk 157-et 100-zal, így kapjuk a 15700 cm-t. Ezért

A fordulatszám = 15700 cm/314 cm

= 50 fordulat.

6. példa

Egy 100 cm hosszú és 50 cm széles téglalap alakú drótdarabot levágunk és kör alakúra hajtunk. Számítsuk ki a kialakult kör kerületét és sugarát.

Megoldás

A kialakult kör kerülete = a téglalap alakú drót kerülete.

Téglalap kerülete = 2(L + W)

= 2(100 + 50) cm

= 2 * 150 cm

= 300 cm.

Ezért a kör kerülete 300 cm lesz.

Most számítsuk ki a sugarát.

Kerület = 2 π R

300 cm = 2 * π * R

300 cm = 2 * 3,14 * R

300 cm = 6,28R

Elosztjuk mindkét oldalt 6,28-al.

R = 47.77 cm

A kör sugara tehát 47,77 cm lesz.

7. példa

Egy motorkerékpár minden egyes kerekének sugara 0. 85 m. Milyen messzire fog elmenni a motorkerékpár, ha minden kerék 1000 fordulatot tesz meg. Tegyük fel, hogy a motorkerékpár egyenesen halad.

Megoldás

Először is keressük meg a kerék kerületét.

Kerület = 2 π R

= 2 * 3,14 * 0,85

= 5,338 m.

A megtett távolság megtalálásához szorozzuk meg a kerék kerületét a megtett fordulatszámmal.

Távolság = 5,338 * 1000

= 5338 m

Ezért a megtett távolság egyenlő 5,338 kilométerrel.

GYakorlati kérdések

1. Egy 12 colos pizzát szolgálnak fel Mike-nak és barátainak. Mike-ot a kerületének kiszámítása érdekli. Segíts neki!
2. Egy adott négyzet kerülete 1/3-a egy adott kör területének. Ha a négyzet hossza L egység, határozzuk meg a kör átmérőjét L-hez viszonyítva.

Válaszok

1. 12π hüvelyk vagy 37,67 hüvelyk
2. 12L/π egység

Előző lecke | Főoldal | Következő lecke