2.12: Van der Waals-egyenlet

A van der Waalsnak köszönhető egyenlet egyszerű módon bővíti az ideális gázegyenletet. Van der Waals egyenlete

\

Ez jobban illeszkedik egy valós gáz nyomás-térfogat-hőmérséklet adataira, mint az ideális gázegyenlet. A jobb illeszkedés két paraméter (a\(a\) és a\(b\)) bevezetésével érhető el, amelyeket minden egyes gáz esetében kísérletileg kell meghatározni. A Van der Waals-egyenlet különösen hasznos a valódi gázok viselkedésének megértésére irányuló törekvéseinkben, mert egyszerű fizikai képet testesít meg a valódi gáz és az ideális gáz közötti különbségről.

A Boyle-törvény Newton-törvényekből való levezetése során feltételezzük, hogy a gázmolekulák nem lépnek kölcsönhatásba egymással. Egyszerű érvekből kiderül, hogy ez csak közelítőleg lehet igaz. A valódi gázmolekuláknak kölcsönhatásba kell lépniük egymással. Rövid távolságokon taszítják egymást. Valamivel nagyobb távolságokon vonzzák egymást. Az ideális gáz egyenlete a statisztikai termodinamika elméletének alkalmazásával is levezethető a 10. §-ban tett alapfeltevésekből. A molekulák tulajdonságaira vonatkozó különböző feltételezésekkel a statisztikai termodinamikát alkalmazva levezethetjük a\({}^{5}\) van der Waals-egyenletet. A szükséges feltételezések a következők: a molekulák véges térfogatot foglalnak el, és olyan erővel vonzzák egymást, amely a köztük lévő távolság hatványának inverzeként változik. (A vonzóerőt általában \(r^{-6}\) arányosnak szokták feltételezni.)

Ahhoz, hogy felismerjük, hogy a valódi gázmolekulák egyszerre vonzzák és taszítják egymást, csak arra kell emlékeznünk, hogy bármely gáz cseppfolyósítható a hőmérséklet csökkentésével és a rá gyakorolt nyomás növelésével. Ha a folyadékot tovább hűtjük, akkor szilárddá fagy. Nos, a szilárd anyag két megkülönböztető jellemzője, hogy megtartja alakját, és hogy szinte összenyomhatatlan. A szilárd anyag összenyomhatatlanságát az alkotó molekulák közötti taszító erőknek tulajdonítjuk; ezek olyan közel kerültek egymáshoz, hogy a köztük lévő taszító erők fontossá váltak. Ahhoz, hogy a szilárd testet összenyomjuk, a molekulákat még közelebb kell tolni egymáshoz, amihez rendkívüli erőre van szükség. Másrészt, ha egy jégkockát átdobunk a szobán, az azt alkotó vízmolekulák együtt repülnek át a szobán. Nyilvánvaló, hogy a szilárd testben lévő vízmolekulák vonzzák egymást, különben mindannyian külön utakon járnának – a jégkocka eldobása olyan lenne, mintha egy marék száraz homokot dobnánk el. A vízmolekulák azonban a hőmérséklettől és a nyomástól függetlenül ugyanazok a molekulák, így ha a szilárd halmazállapotban vonzó és taszító erők vannak közöttük, akkor ezeknek az erőknek a folyadék- és gázfázisban is jelen kell lenniük.

A gázfázisban a molekulák távol vannak egymástól; a folyékony vagy a szilárd halmazállapotban viszont egymáshoz vannak szorítva. Forráspontján a folyadék térfogata sokkal kisebb, mint annak a gáznak a térfogata, amelyből kondenzálódott. A fagyásponton a szilárd anyag térfogata csak kis mértékben különbözik annak a folyadéknak a térfogatától, amelyből megfagyott, és biztosan nagyobb, mint nulla. Ezek a hétköznapi megfigyelések könnyen megmagyarázhatók, ha feltételezzük, hogy minden molekulának van egy jellegzetes térfogata. Ezt viszont a molekulák közötti erők természetének következményeként értelmezhetjük; nyilvánvaló, hogy ezek az erők a molekulapárok közötti távolság csökkenésével egyre erősebbek. Mivel egy folyadék vagy egy szilárd anyag meghatározott térfogatot foglal el, a taszító erőnek gyorsabban kell növekednie, mint a vonzó erőnek, amikor a molekulák közötti távolság kicsi. Gyakran hasznos egy kondenzált fázis moláris térfogatáról beszélni. A moláris térfogat alatt egy tiszta anyag egy móljának térfogatát értjük. Egy kondenzált fázis moláris térfogatát az a molekulák közötti távolság határozza meg, amelynél a molekulák közötti vonzó és taszító erők között egyensúly van.

A kondenzált fázisokban a molekulák nyilvánvalóan nagyon közel vannak egymáshoz. Ha feltételezzük, hogy a molekulák közötti üres terek elhanyagolhatóak, akkor a kondenzált fázis térfogata megközelítőleg megegyezik a mintában lévő molekulák számának és az egyetlen molekula térfogatának szorzatával. Ekkor a moláris térfogat az Avogadro-szám szorozva az egy molekula által elfoglalt térfogattal. Ha ismerjük a sűrűséget, D, és a moláris tömeget, \(\overline{M}\), akkor a moláris térfogatot, \(\overline{V}\), a következőképpen találhatjuk meg:

\

Az egy molekula által elfoglalt térfogat, V\({}_{molekula}\), lesz

\

A van der Waals-egyenletben megjelenő nyomás és térfogat a valós gáz nyomása és térfogata. A van der Waals-egyenletben szereplő kifejezéseket kapcsolatba hozhatjuk az ideális gázegyenlettel: Hasznos, ha a \(\left(P+{{an}^2}/{V^2}\right)\) és \(\left(V-nb\right)\) kifejezéseket egy feltételezett ideális gáz nyomásának és térfogatának tekintjük. Vagyis

\ &=nRT \end{align*}\]

Ezután

\

Az ideális gáz egyenletét egy olyan modellből vezetjük le, amelyben a molekulák nem kölcsönható pontszerű tömegek. Az ideális gáz térfogata tehát az olyan gáz által elfoglalt térfogat, amelynek egyes molekulái nulla térfogatúak. Ha egy valós gáz egyes molekulái ténylegesen \({b}/{\overline{N}}}\) térfogatot foglalnak el, akkor \(n\) móljuk ténylegesen \(n\) térfogatot foglal el

\

Van der Waals egyenlete szerint a valós gáz térfogata az a térfogat, amelyet nem kölcsönható pontszerű tömegek foglalnának el, \(V_{ideális\ gáz}\), plusz maguk a gázmolekulák tényleges térfogata. (Amikor valós gázmolekulákra vonatkozó adatokat illesztünk a van der Waals-egyenlethez, az \(b\) értéke általában valamivel nagyobb, mint a folyadék sűrűségéből és molekulatömegéből becsült térfogat. Lásd a 24. feladatot.)

Hasonlóképpen

\

Ezt a valós gáz molekulái közötti vonzó kölcsönhatások logikus következményeként értelmezhetjük. Az \(a>0\) azt mondja, hogy a valós gáz nyomása kisebb, mint a hipotetikus ideális gáz nyomása, mégpedig olyan mértékben, amely arányos \({\left({n}/{V}\right)}^2\). Az arányossági állandó \(a\). Mivel \({n}/{V}\) a gázmolekulák moláris sűrűsége (mol per térfogategység), ez a koncentráció mértékegysége. Az azonos fajtájú molekulák közötti ütközések száma arányos a koncentráció négyzetével. (Ezt a pontot részletesebben a 4. és 5. fejezetben tárgyaljuk.) Tehát \({\left({n}/{V}\right)}^2\) annak a gyakoriságnak a mértéke, amellyel a valódi gázmolekulák egymással szoros kapcsolatba kerülnek. Ha egymáshoz közeledve vonzzák egymást, akkor ennek a vonzásnak a hatásának arányosnak kell lennie \({\\left({n}/{V}\right)}^2\). Van der Waals egyenlete tehát összhangban van azzal az elképzeléssel, hogy a valós gáz nyomása a vonzó kölcsönhatások gyakoriságával és erősségével arányos mértékben különbözik a hipotetikus ideális gáz nyomásától.

De miért van a vonzó kölcsönhatásoknak ilyen hatása; miért kell a valós gáz nyomásának kisebbnek lennie, mint a hipotetikus ideális gázé? Talán a legjobb módja a minőségi kép kialakításának, ha felismerjük, hogy a vonzó molekulák közötti erők hajlamosak arra, hogy a gázmolekulák összecsomósodjanak. Végül is ezek a vonzóerőkvonzóerő az, ami miatt a molekulák alacsony hőmérsékleten folyadékká tömörülnek. A forráspont felett a gázmolekulák azon képessége, hogy külön utakon járjanak, korlátozza ennek a tendenciának a hatását; azonban a vonzóerőknek még a gázban is úgy kell hatniuk, hogy a molekulák által elfoglalt térfogat csökkenésére törekedjenek. Mivel a gáz által elfoglalt térfogatot a tartály mérete határozza meg – nem pedig magának a gáznak a tulajdonságai -, ez a csomósodási tendencia a nyomás csökkenéseként jut kifejezésre.

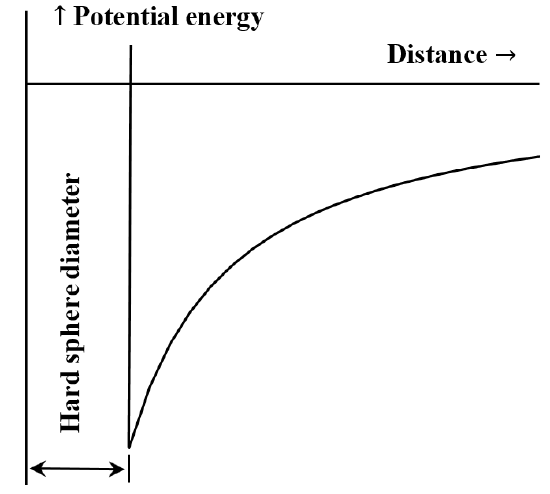
A részecskék vagy kémiai részek közötti kölcsönhatást gyakran hasznos a potenciális energia és a távolság diagramjával leírni. A van der Waals-egyenlet megfelel annak az esetnek, amikor a molekulák közötti taszító kölcsönhatás nem létezik, amíg a molekulák nem érintkeznek. Amint érintkezésbe kerülnek, az egymáshoz való közeledésükhöz szükséges energia tetszőlegesen nagy lesz. Ezt gyakran azzal írják le, hogy “kemény gömbökként” viselkednek. A két molekula közötti vonzóerő a távolság növekedésével csökken. Ha nagyon távol vannak egymástól, a vonzó kölcsönhatás nagyon kicsi. Azt mondjuk, hogy a kölcsönhatás energiája nulla, ha a molekulák végtelenül távol vannak egymástól. Ha kezdetben két egymástól távol eső, helyhez kötött, egymást kölcsönösen vonzó molekulánk van, akkor spontán módon egymás felé fognak mozogni, menet közben kinetikus energiát nyerve. Potenciális energiájuk csökken, ahogy közelednek egymáshoz, és akkor éri el a legkisebb értékét, amikor a molekulák érintkeznek. Így a van der Waals-egyenletből következik az 5. ábrán vázolt potenciális energia-távolság diagram

.