Funções ou Mapeamento

Agora, em funções ou mapeamento vamos estudar sobre o tipo especial de relações chamadas funções ou mapeamento. Para entendê-las, vamos tomar alguns exemplos da vida real.

Todas estas questões têm
respostas únicas. Vamos
ver como podemos relacionar
isto no mapeamento da aprendizagem.

● De onde nasce o sol?

Este

● Qual é a capital da Índia?

Delhi

● Qual é o sucessor de 4?

5

● Qual é a soma de 5 e 3?

8

Mapa ou Funções:

Se A e B são dois conjuntos não vazios, então uma relação ‘f’ do conjunto A para o conjunto B é dita ser uma função ou mapeamento,
● Se cada elemento do conjunto A está associado a um elemento único do conjunto B.

● A função ‘f’ do conjunto A para B é denotada por f : A → B.

● Se f é uma função de A a B e x ∈ A, então f(x) ∈ B onde f(x) é chamada a imagem de x sob f e x é chamada a pré imagem de f(x) sob ‘f’.

Nota:

Para f ser um mapeamento de A a B:

● Cada elemento de A deve ter imagem em B. Figura adjacente não representa um mapeamento já que o elemento d no conjunto A não está associado a nenhum elemento do conjunto B.

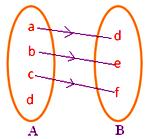
● Nenhum elemento de A deve ter mais de uma imagem. Figura adjacente não representa um mapeamento uma vez que o elemento b do conjunto A está associado a dois elementos d, f do conjunto B.

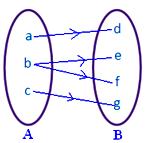
● Diferentes elementos de A podem ter a mesma imagem em B. A figura adjacente representa um mapeamento.

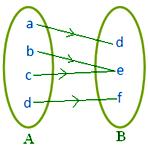
Nota:

>Todos os mapeamentos são uma relação, mas todas as relações podem não ser um mapeamento.

Função como um tipo especial de relação:

Vamos relembrar e rever a função como um tipo especial de relação suponha, A e B são dois conjuntos não vazios, então uma regra ‘f’ que associa cada elemento de A com um elemento único de B é chamada de função ou um mapeamento de A para B.
Se ‘f’ é um mapeamento de A para B,

exprimimo-lo como f: A → B

lemos como ‘f’ é uma função de A para B.
Se ‘f’ é uma função de A para B e x∈A e y∈B, então dizemos que y é a imagem do elemento x sob a função ‘ f ‘ e o denotamos por f(x).
Então, escrevemos como y = f(x)

Aqui, o elemento x é chamado de pré-imagem de y.

Assim, para uma função de A a B.
● A e B devem ser não vazios.

● Cada elemento de A deve ter imagem em B.

● Nenhum elemento de ‘A’ deve ter mais do que uma imagem em ‘B’.
Nota:

● Dois ou mais elementos de A podem ter a mesma imagem em B.

● f : x → y significa que sob a função de ‘f’ de A a B, um elemento x de A tem imagem y em B.

● É necessário que cada imagem f esteja em B, mas pode haver alguns elementos em B que não sejam imagens f de nenhum elemento de A.

● Relações e Mapeamento

Par ordenado

Produto cartesiano de dois conjuntos

Relação

Domínio e alcance de uma relação

Funções ou Mapeamento

Co-domíniodomínio e alcance da função

● Relações e Mapeamento – Folhas de trabalho

Folha de trabalho sobre relação matemática

Folha de trabalho sobre funções ou mapeamento

Problemas de Matemática do 7º Grau

Prática de Matemática do 8º Grau
De Funções ou Mapeamento para PÁGINA INICIAL