Articles

Somme de produit (SOP) & produit de somme (POS)

On novembre 10, 2021 by admin

Produit de somme (POS) &Somme de produit (SOP)

Somme de produit (SOP)

Somme de produit est la forme abrégée de SOP. La forme somme de produit est une forme d’expression en algèbre booléenne dans laquelle différents termes produits des entrées sont additionnés. Ce produit n’est pas une multiplication arithmétique mais c’est un ET logique booléen et la somme est un OU logique booléen.

Pour mieux comprendre le SOP, nous devons connaître le terme min.

Terme min

Minterm signifie le terme qui est vrai pour un nombre minimum de combinaison d’entrées. C’est vrai pour une seule combinaison d’entrées.

Puisque la porte ET donne aussi Vrai seulement quand toutes ses entrées sont vraies alors on peut dire que les min termes sont ET des combinaisons d’entrées comme dans le tableau donné ci-dessous.

3 entrées ont 8 combinaisons différentes. Chaque combinaison a un minterme dénoté par le petit m et son numéro décimal de combinaison écrit en indice. Chacun de ces mintermes ne sera vrai que pour la combinaison d’entrée spécifique.

• Vous pouvez également lire : Compteur asynchrone numérique (compteur d’ondulation) – Types, fonctionnement & Application

Types de formes de somme de produits (SOP)

Il existe quelques formes différentes de somme de produits.

• Forme SOP canonique
• Forme SOP non canonique
• Forme SOP minimale

Forme SOP canonique

C’est la forme standard de la somme de produits. Elle est formée par O Ring les minterms de la fonction pour laquelle la sortie est vraie. Elle est également connue sous le nom de Somme des termes mineurs ou forme normale disjonctive canonique (CDNF). Il s’agit simplement d’un nom fantaisiste. « canonique » signifie « normalisée » et « disjonctive » signifie « union logique OU ».

L’expression SOP canonique est représentée par le signe de sommation ∑ et les termes mineurs dans les accolades pour lesquels la sortie est vraie.

Par exemple, une table de vérité de fonctions est donnée ci-dessous.

Pour cette fonction, l’expression SOP canonique est

F = ∑( m1, m2, m3, m5 )

ce qui signifie que la fonction est vraie pour les mintermes {1, 2, 3, 5}.

En développant la sommation, on obtient .

F = m1 + m2 + m3 + m5

Maintenant en mettant les termes min dans l’expression

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

La forme canonique contient toutes les entrées complémentées ou non complémentées dans ses termes produits.

Vous pouvez également lire : Compteur synchrone numérique – Types, fonctionnement & Applications

Forme SOP non canonique

Comme son nom l’indique, cette forme est la forme non standardisée des expressions SOP. Les termes produits ne sont pas les termes min mais ils sont simplifiés. Prenons comme exemple la fonction ci-dessus sous forme canonique.

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = A̅B̅C + A̅B(C̅ + C) + AB̅C

F = A̅B̅C + A̅B(C̅ + C) + AB̅C

F = A̅B̅C + A̅B(C̅ + C). A̅B(1) + AB̅C

F = A̅B̅C + A̅B + AB̅C

Cette expression est toujours sous forme de somme de produits mais c’est une forme nonforme canonique ou non normalisée.

Forme SOP minimale

Cette forme est l’expression SOP la plus simplifiée d’une fonction. C’est également une forme non canonique. La forme SOP minimale peut être réalisée à l’aide de théorèmes algébriques booléens mais elle est très facilement réalisée à l’aide de la carte de Karnaugh (K-map).

La forme SOP minimale est préférée car elle utilise le nombre minimal de portes et de lignes d’entrée. elle est commercialement avantageuse en raison de sa taille compacte, de sa vitesse rapide et de son faible coût de fabrication.

Prenons un exemple de la fonction donnée ci-dessus sous forme canonique.

Sa carte K est donnée ci-dessous.

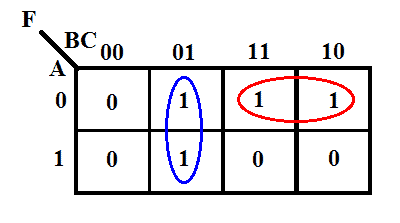
Selon la carte K, l’expression de sortie sera

F = B̅C + A̅B

C’est l’expression optimisée la plus simplifiée & pour ladite fonction. Cette expression ne nécessite que deux portes ET à 2 entrées &une porte OU à 2 entrées. Cependant, la forme canonique nécessite quatre portes ET à 3 entrées &une porte OU à 4 entrées, ce qui est relativement plus coûteux que la mise en œuvre de la forme minimale.

• Vous pouvez également lire : Compteur en anneau & Compteur Johnson – Construction & Fonctionnement

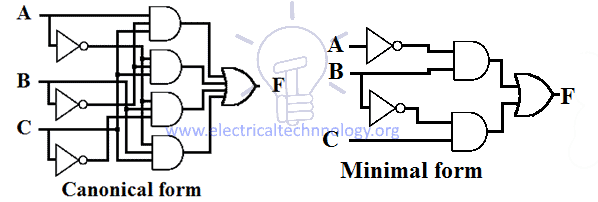
Conception schématique de la somme de produit (SOP)

L’expression SOP met en œuvre une conception ET-OU à 2 niveaux dans laquelle la porte de 1er niveau est une porte ET suivant la porte de 2ème niveau qui est une porte OU. La conception schématique de l’expression SOP a besoin d’un tableau de groupe de portes ET &une porte OU.

Chaque expression SOP a un peu la même conception, c’est-à-dire que toutes les entrées passent par une porte ET et ensuite la sortie de ces portes ET passe par une porte OU comme le montre la figure donnée ci-dessous.

Le nombre d’entrées et le nombre de portes ET dépendent de l’expression que l’on met en œuvre.

Un exemple de conceptions d’expression SOP canonique et minimale pour une fonction est donné ci-dessous.

Conversion de la forme SOP minimale à la forme SOP canonique

La conversion de la forme minimale ou de toute sorte de forme non canonique à la forme canonique est très simple.

Comme nous le savons la forme canonique a des termes minuscules & Les termes minuscules sont constitués de toutes les entrées soit complétées soit non complétées. Ainsi, nous allons multiplier chaque terme du SOP minimal avec la somme de la forme complétée et non complétée de l’entrée manquante. Un exemple de conversion pour la fonction ci-dessus sous forme de SOP minimal est donné ci-dessous.

Forme SOP minimal

F = A̅B + B̅C

Le terme A̅B est l’entrée manquante C. Donc nous allons multiplier A̅B avec (C+C̅) parce que (C+C̅ = 1). Le terme B̅C est l’entrée manquante A. Il sera donc multiplié par (A+A̅)

F = A̅B(C + C̅) + B̅C(A + A̅)

F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C

Maintenant, cette expression est sous forme canonique.

Conversion de la POS canonique en POS canonique

L’expression SOP standard peut être convertie en expression POS (produit de la somme) standard. Par exemple, la fonction donnée ci-dessus est sous forme POS canonique

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = ∑ ( m1, m2, m3, m5 )

Les termes restants de cette fonction sont des maxtermes pour lesquels la sortie est fausse. Ces termes max sont M0,M4,M6,M7. Ces termes max seront utilisés dans l’expression POS comme le produit de ces termes max. Le symbole du produit est ∏.

F = ∏ ( M0, M4, M6, M7)

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

Les termes max sont le complément des termes minterms. C’est pourquoi M0=(A+B+C).

• Vous pouvez aussi lire : Ripple Carry And Carry Look Ahead Adder

Conversion du SOP canonique en SOP minimal

Le SOP canonique peut être converti en SOP minimal. Il peut être converti en utilisant la carte de Karnaugh ou les théorèmes algébriques booléens. La méthode de la carte de Karnaugh est très facile et son exemple a été fait ci-dessus dans la forme SOP minimale.

Produit de la somme

Produit de la somme abrégé pour POS.

La forme produit de la somme est une forme dans laquelle les produits de différents termes de somme des entrées sont pris. Il ne s’agit pas de produit et de somme arithmétiques mais respectivement de ET et de OU booléens logiques.

Pour mieux comprendre le produit de somme, nous devons connaître le terme Max.

Terme Max

Maxterm désigne le terme ou l’expression qui est vrai pour un nombre maximal de combinaisons d’entrées ou qui est faux pour une seule combinaison d’entrées.

Puisque la porte OU donne également faux pour une seule combinaison d’entrées. Donc Maxterm est OR de soit des entrées complémentaires ou non complémentaires.

Les termes maximaux pour 3 variables d’entrée sont donnés ci-dessous.

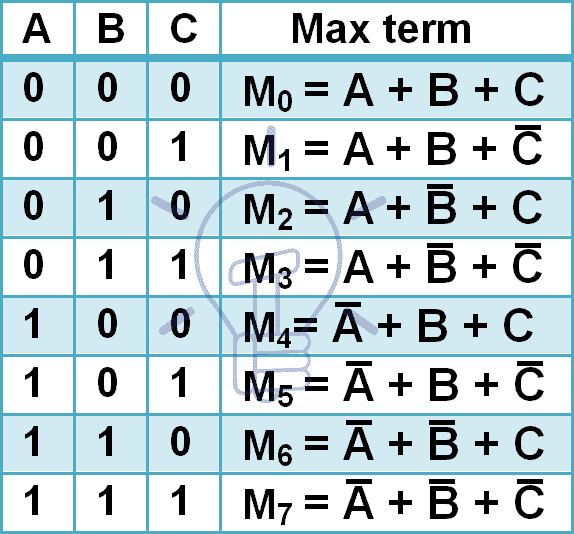
3 entrées ont 8 combinaisons différentes donc il aura 8 maxterms. Les maxterms sont dénotés par la majuscule M et le numéro de combinaison décimal Dans l’indice comme indiqué dans le tableau donné ci-dessus.

Dans le maxterm, chaque entrée est complétée parce que Maxterm donne ‘0’ seulement quand la combinaison mentionnée est appliquée et Maxterm est le complément de minterm.

M3 = m̅3

M3 = (A̅BC)’

M3 = A + B̅ +C̅ DE loi de Morgan

C’est pourquoi pour A=0 le terme maximum consiste en A & pour A=1 le terme maximum consiste en A̅.

Vous pouvez également lire : Les bascules numériques – bascules SR, D, JK et T

Types de formes de produit de somme

Il existe différents types de formes de produit de somme.

• Forme POS canonique
• Forme non – canonique
• Forme POS minimale

Forme POS canonique

Elle est également connue sous le nom de Produit du terme Max ou Forme normale conjonctive canonique (CCNF). Canonique signifie standard et conjonctif signifie intersection.

Dans cette forme, les Maxterms sont AND ensemble pour lesquels la sortie est fausse.

L’expression POS canonique est représentée par ∏ et les Maxterms pour lesquels la sortie est fausse entre parenthèses comme le montre l’exemple donné ci-dessous.

F = ∏ (M0, M4, M6, M7)

Expansion du produit

F = M0.M4.M6.M7

Mettre les termes Max

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

La forme canonique contient toutes les entrées complémentées ou non complémentées dans son chaque terme Somme.

• Vous pouvez également lire : Clap Switch Circuit Electronic Project Using 555 Timer

Forme non – canonique

Le produit d’une expression de somme qui n’est pas sous forme standard est appelé forme non canonique.

Prenons la fonction donnée ci-dessus comme exemple.

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

F = (B+C) (A̅+B̅+C)(A̅+B̅+C̅)

.

Mêmes termes mais inversés élimine de deux termes Max et forme un seul terme pour le prouver voici un exemple.

= (A+B+C) (A̅+B+C)

= AA̅+AB+AC+A̅B+BB+BC+A̅C+BC+CC

= 0+AB+AC+A̅B+A̅C+B+BC+C

= A(B+C)+A̅(B+C)+B(1+C)+C

.

= (B+C)(A+A̅)+B(1)+C

= (B+C)(0)+B+C

= B+C

L’expression obtenue est toujours sous forme de Produit de la Somme mais c’est une forme nonforme non canonique.

Forme POS minimale

C’est la forme la plus simplifiée et optimisée d’une expression POS qui est non canonique. La forme minimale de produit de somme peut être obtenue en utilisant des théorèmes d’algèbre booléenne comme dans l’exemple non canonique donné ci-dessus. Une autre méthode pour atteindre la forme POS minimale est d’utiliser la carte de Karnaugh qui est comparativement plus facile que l’utilisation des théorèmes algébriques booléens.

La forme POS minimale utilise moins d’entrées et de portes logiques pendant sa mise en œuvre, c’est pourquoi ils sont préférés à la forme canonique pour leur mise en œuvre compacte, rapide et à faible coût.

Prenons comme exemple la fonction donnée ci-dessus

Carte K de la fonction

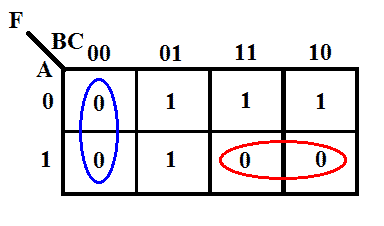
Expression minimale utilisant la carte K

F = (B+C) (A̅+B̅)

L’expression obtenue est le produit minimal de la forme somme. Il s’agit toujours du produit de l’expression de la somme, mais il ne nécessite que 2 entrées deux portes OU et une seule porte ET à 2 entrées. Cependant, la forme canonique nécessite 4 portes OU de 3 entrées et 1 porte ET de 4 entrées.

• Vous pouvez également lire : Systèmes d’amplificateurs à rétroaction négative et à rétroaction négative

Conception schématique du produit de la somme (POS)

L’expression du produit de la somme a une conception schématique spécifique de OR-AND. Dans OR-AND, les entrées passent par un tableau de portes OR qui est le premier niveau de portes, la sortie des portes OR de premier niveau passe par le deuxième niveau de la porte,qui est une porte AND.

Le nombre d’entrées et le nombre de portes utilisés dans cette conception dépend de l’expression qui doit être mise en œuvre.

La forme canonique se compose du nombre maximum d’entrées et de portes possibles,cependant, la forme minimale se compose du plus petit nombre possible d’entrées et de portes. La conception schématique de la forme POS canonique et minimale est donnée ci-dessous.

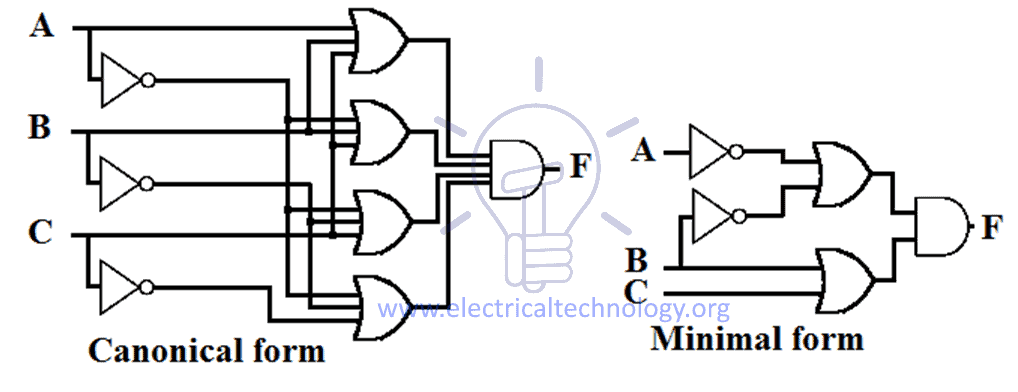
Conversion de POS minimal en POS de forme canonique

Comme nous le savons la forme canonique de POS a des termes max et les termes max contiennent chaque entrée soit complétée ou non complétée. Nous allons donc ajouter chaque terme de la somme avec le produit de l’entrée manquante complétée et non complétée. Un exemple de sa conversion est donné ci-dessous.

Forme POS minimale

F = (A̅+B̅) (B+C)

(A̅+B̅) terme est l’entrée C manquante donc nous allons ajouter (CC̅) avec elle. (B+C) terme manque l’entrée A donc nous ajouterons (AA̅) avec lui.

F = (A̅+B̅+CC̅) (B+C+AA̅)

F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)(A̅+B+C)

Cette expression est maintenant sous forme canonique.

• Vous pouvez également lire : Compteur et types de compteurs électroniques

Conversion de POS canonique en POS

Le produit d’une expression de somme peut être converti en forme de somme de produits seulement si l’expression est sous forme canonique. Le POS canonique et le SOP canonique sont inter-convertibles c’est-à-dire qu’ils peuvent être convertis l’un en l’autre. Un exemple de conversion de POS en SOP est donné ci-dessous.

Forme canonique POS

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

Dans la forme canonique, chaque terme de la somme est un terme max donc on peut aussi l’écrire comme :

F = ∏(M0,M4,M6,M7)

Les combinaisons d’entrées restantes sont des mintermes de la fonction pour lesquels sa sortie est vraie. Pour la convertir en expression SOP, nous allons d’abord changer le symbole en sommation (∑) et utiliser le minterm restant.

F = ∑ (m1,m2,m3,m5)

Maintenant nous allons développer le signe de sommation pour former une expression SOP canonique.

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

Les termes Min sont le complément des termes Max pour la même combinaison d’entrées.

POS canonique à minimal

Un produit canonique d’expression de somme peut être converti en produit minimal de forme de somme en utilisant la carte de Karnaugh (K-map). Une autre méthode pour convertir canonique en minimal est d’utiliser des théorèmes d’algèbre booléenne.

L’utilisation de K-map est très facile c’est pourquoi K-map est préféré. Pour l’expression POS minimale, les 0 dans K-map sont combinés en groupes et l’expression que nous obtenons est complétée puisque les groupes ont été faits de ‘0’. Son exemple a été fait ci-dessus.

Vous pouvez également lire:

• Porte logique numérique NOT – Porte logique numérique inverseur
• Porte logique numérique exclusif-NOR (XNOR)
• Porte logique numérique NOR
• Porte logique numérique NAND

.