» Quelle est la taille d’une cellule d’E. coli et quelle est sa masse ?

Combien est grande une cellule de E. coli et quelle est sa masse ?

Mode de lecture

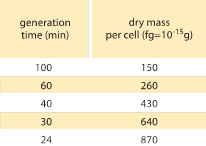
Tableau 1 : Relation entre la masse bactérienne et le temps de division. La masse sèche par cellule est donnée en fonction du temps de génération (doublement). Il est suggéré que la masse augmente de façon à peu près exponentielle avec le taux de croissance, comme cela a été observé à l’origine par M. Schaechter et al J. Gen. Microbiol., 19:592, 1958. Le poids sec des cellules a été calculé en utilisant une valeur de 173 µg par unité OD460 d’un mL (BNID 106437). La souche utilisée est B/r, une souche couramment utilisée dans les premières études de physiologie bactérienne. Valeurs tirées de F. C. Neidhardt, « Escherichia coli and Salmonella : Cellular and Molecular Biology », Vol. 1., Chapter 3, ASM Press, 1996.

La taille d’une bactérie typique telle que E. coli sert de règle standard pratique pour caractériser les échelles de longueur en biologie moléculaire et cellulaire. Une « règle empirique » basée sur des générations de mesures en microscopie optique et électronique pour les dimensions d’une cellule d’E. coli consiste à lui attribuer un diamètre d’environ ≈1µm, une longueur de ≈2µm et un volume de ≈1µm3 (1 fL) (BNID 101788). La forme peut être approximée comme un sphérocylindre, c’est-à-dire un cylindre avec des chapeaux hémisphériques. Compte tenu du diamètre et de la longueur cités, nous pouvons calculer une estimation plus fine du volume de ≈1,3 µm3 (5π/12 pour être précis). La différence entre cette valeur et la valeur de la règle empirique citée ci-dessus montre le niveau d’incohérence avec lequel nous vivons confortablement lorsque nous utilisons des règles empiriques. L’une des voies les plus simples pour parvenir à une estimation de la masse d’une bactérie consiste à exploiter le volume de ≈1 µm3 d’une cellule d’E. coli et à supposer qu’elle a la même densité que l’eau. Cette estimation naïve aboutit à une autre valeur standard, à savoir qu’une bactérie telle que E. coli a une masse de ≈1 pg (pico=10-12). Comme la plupart des cellules sont constituées d’environ 2/3 d’eau (BNID 100044, 105482) et que les autres composants, comme les protéines, ont une densité caractéristique d’environ 1,3 fois la densité de l’eau (BNID 101502, 104272), la conversion du volume cellulaire en masse est précise à environ 10%.

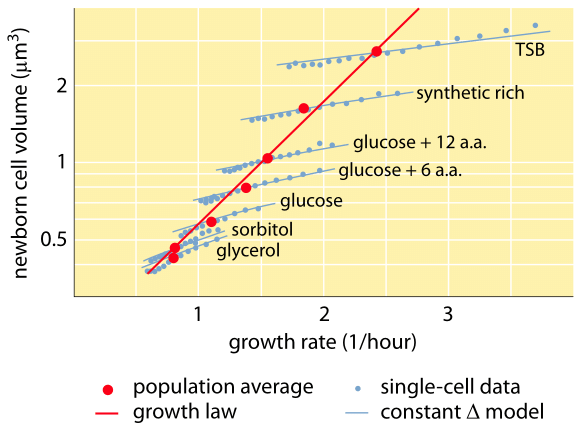
Fig. 1 : Relation entre le volume cellulaire et le taux de croissance. En utilisant la microscopie et les dispositifs microfluidiques, le volume cellulaire peut être mesuré au niveau de la cellule unique dans diverses conditions, confirmant que le volume cellulaire moyen croît exponentiellement avec le taux de croissance. En revanche, la variation entre les cellules pour une condition donnée évolue différemment. La variation du comportement d’une seule cellule est utilisée pour tester des modèles de régulation de la taille des cellules. (Adapté de S. Taheri-Araghi et al., Curr. Biol. 25:385, 2015.)

L’un des résultats classiques de la physiologie bactérienne souligne que la plasticité des propriétés des cellules découle de la dépendance de la masse cellulaire au taux de croissance. En d’autres termes, des taux de croissance plus rapides sont associés à des cellules plus grandes. Cette observation fait référence aux changements physiologiques où les milieux qui augmentent le taux de croissance produisent également des cellules plus grandes, comme le montre la figure 1. Cela s’est également avéré vrai sur le plan génétique, puisque les études d’évolution expérimentale à long terme qui ont conduit à des taux de croissance plus rapides ont montré des volumes cellulaires plus importants (BNID 110462). De telles observations nous aident à dissiper le mythe de « la cellule » – où les gens, souvent sans le vouloir, utilisent les mesures d’une cellule pour faire des déductions sur d’autres types de cellules ou sur le même type de cellules dans des conditions différentes. Les études classiques de Dennis et Bremer ont systématisé ces mesures et constaté que la masse sèche varie, comme le montre le tableau 1, d’une valeur moyenne de 148 fg pour les cellules se divisant toutes les 100 minutes à 865 fg pour celles dont le temps de division est de 24 minutes, ce qui indique une différence de plus de 5 fois selon le taux de croissance. Une tendance similaire a été observée dans d’autres organismes (par exemple pour la levure bourgeonnante, BNID 105103). À environ 70 % d’eau, ces valeurs correspondent à une fourchette d’environ 0,4 à 2,5 µm3 en termes de volume. Comment peut-on justifier des tailles plus grandes pour des cellules se développant à des vitesses plus élevées ? Cette question fait encore l’objet de débats à ce jour (Molenaar D. et al. MSB 5:323, 2009 ; Amir, A., Phys. Rev, Let., 112:208102, 2014). Les explications varient, allant de la suggestion d’un avantage dans la façon dont l’allocation des ressources est faite à l’affirmation qu’il ne s’agit en fait que d’un effet secondaire de l’existence d’une période intégrée d’environ 60 minutes entre le moment où une cellule décide qu’elle a accumulé suffisamment de masse pour commencer les préparatifs de la division et celui où elle termine la réplication de l’ADN et l’acte de division. Cette période de « retard » à peu près constante conduit à une dépendance exponentielle de la masse cellulaire moyenne par rapport au taux de croissance dans ce type de raisonnement (Amir, A., Phys. Rev, Let, 112:208102, 2014).

Les méthodes de mesure du volume cellulaire vont de l’utilisation d’un compteur Coulter ((BNID 100004), qui déduit le volume en fonction des changements de résistance d’un petit orifice lorsqu’une cellule y passe, à des mesures plus directes utilisant la microscopie à fluorescence qui jauge la longueur et le diamètre des cellules dans différentes conditions (figure 1 et BNID 106577, 111480). De manière surprenante, le fait que différents laboratoires ne convergent pas toujours vers les mêmes valeurs peut être dû à des différences dans les méthodes d’étalonnage ou dans les souches et les conditions de croissance exactes. Une capacité sans précédent de mesurer la masse cellulaire est obtenue en pesant efficacement les cellules sur un cantilever microscopique. Comme l’illustre la figure 2A, un flux de fluide est utilisé pour forcer une cellule à aller et venir dans le cantilever creusé. La mesure exploite le fait que la masse de la cellule affecte la fréquence d’oscillation du cantilever. Cette fréquence peut être mesurée avec une précision phénoménale et utilisée pour déduire les masses avec une précision de l’ordre du femtogramme. En changeant la direction du flux de liquide, la cellule est piégée pendant des minutes ou plus et son taux d’accumulation de masse est mesuré en continu au niveau de la cellule unique. Lors de la première application de cette technique, il a été démontré que les cellules uniques plus grandes accumulent également leur masse plus rapidement, ce qui a permis d’éclaircir une question de longue date : la croissance cellulaire est-elle linéaire avec le temps ou plutôt décrite par une tendance approximativement exponentielle ? Les différences peuvent être infimes, mais avec ces capacités révolutionnaires, il a été clairement vu que ce dernier scénario représente mieux la situation dans plusieurs types de cellules testées, comme le montre la figure 2B.

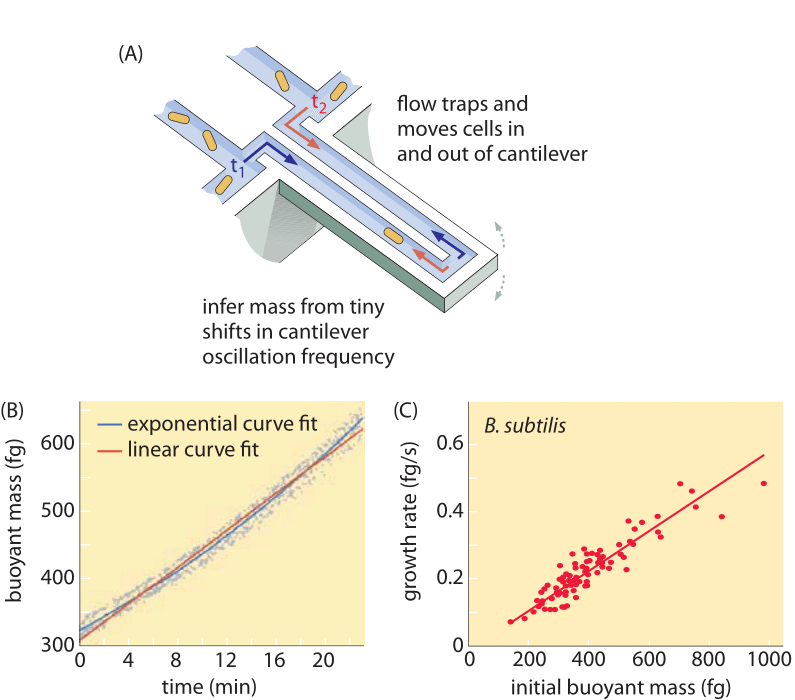
Fig. 2 : Utilisation de la masse flottante pour mesurer la croissance des cellules uniques. (A) Un cantilever à l’échelle du micron oscille à haute fréquence et la masse des cellules peut être déterminée à partir des changements de la fréquence d’oscillation. (B) Mesurée dans le temps, la courbe d’accumulation de la masse d’une seule cellule est représentée. (C) Les cellules de B. subtilis sont représentées ici. Une comparaison entre les prédictions des modèles de croissance linéaire et exponentielle est montrée comme meilleur ajustement. La similitude montre à quel point les deux modèles sont proches sur une plage de seulement deux fois l’augmentation au cours du cycle cellulaire. Le poids sec des cellules correspond à environ 4 fois la masse flottante. (Adapté de M. Godin et al., Nature Meth. 7:387, 2010.)

.