Que faire si vos données ne sont PAS normales ?

Introduction

C’est la semaine d’Halloween, et entre les tours et les friandises, nous, les geeks de données, gloussons sur ce mème mignon sur les médias sociaux.

Vous pensez que c’est une blague ? Laissez-moi vous dire que ce n’est pas une plaisanterie. C’est effrayant, fidèle à l’esprit d’Halloween !

Si nous ne pouvons pas supposer que la plupart de nos données (d’origine commerciale, sociale, économique ou scientifique) sont au moins approximativement « Normales » (c’est-à-dire qu’elles sont générées par un processus gaussien ou par une somme de plusieurs de ces processus), alors nous sommes condamnés !

Voici une liste extrêmement brève de choses qui ne seront pas valables,

• Tout le concept de six-sigma
• La fameuse règle des 68-95-99,7
• Le « saint » concept de p=0,05 (vient de l’intervalle de 2 sigma) en analyse statistique

Souvent assez effrayant ? Parlons-en davantage…

La distribution normale omnipotente et omniprésente

Faisons court dans cette section.

La distribution normale (gaussienne) est la distribution de probabilité la plus connue. Voici quelques liens vers les articles décrivant sa puissance et sa large applicabilité,

• Pourquoi les scientifiques des données aiment la gaussienne

• Comment dominer la partie statistique de votre entretien en sciences des données
• Qu’est-ce qui est si important à propos de la distribution normale ?

En raison de son apparition dans divers domaines et du théorème de la limite centrale (CLT), cette distribution occupe une place centrale dans la science des données et l’analytique.

Alors, quel est le problème ?

C’est tout hunky-dory, quel est le problème ?

Le problème est que souvent vous pouvez trouver une distribution pour votre ensemble de données spécifique, qui peut ne pas satisfaire la normalité c’est-à-dire les propriétés d’une distribution normale. Mais en raison de la surdépendance à l’hypothèse de normalité, la plupart des cadres d’analyse d’entreprise sont conçus sur mesure pour travailler avec des ensembles de données distribuées normalement.

C’est presque ancré dans notre subconscient.

Disons que l’on vous demande de détecter si un nouveau lot de données provenant d’un certain processus (ingénierie ou entreprise) a du sens. Par « avoir du sens », vous voulez dire si les nouvelles données appartiennent c’est-à-dire si elles sont dans la « fourchette attendue ».

Qu’est-ce que cette « attente » ? Comment quantifier la plage ?

Automatiquement, comme s’ils étaient dirigés par une pulsion subconsciente, nous mesurons la moyenne et l’écart-type de l’ensemble de données de l’échantillon et nous procédons à la vérification si les nouvelles données se situent dans une certaine plage d’écarts-types.

Si nous devons travailler avec une limite de confiance de 95%, alors nous sommes heureux de voir les données se situer dans les 2 écarts-types. Si nous avons besoin d’une limite plus stricte, nous vérifions 3 ou 4 écarts types. Nous calculons Cpk, ou nous suivons les directives de six-sigma pour le niveau de qualité ppm (parties par million).

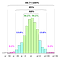
Tous ces calculs sont basés sur l’hypothèse implicite que les données de la population (PAS l’échantillon) suivent une distribution gaussienne, c’est-à-dire que le processus fondamental, à partir duquel les données de la population sont calculées, est le processus de base.c’est-à-dire que le processus fondamental, à partir duquel toutes les données ont été générées (dans le passé et au présent), est régi par le modèle du côté gauche.

Mais que se passe-t-il si les données suivent le modèle du côté droit ?

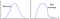
Ou, ceci, et… cela ?

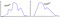
Y a-t-il une borne plus universelle lorsque les données ne sont PAS normales ?

En fin de compte, nous aurons toujours besoin d’une technique mathématiquement solide pour quantifier notre borne de confiance, même si les données ne sont pas normales. Cela signifie que notre calcul peut changer un peu, mais nous devrions toujours être en mesure de dire quelque chose comme ceci-

« La probabilité d’observer un nouveau point de données à une certaine distance de la moyenne est telle et telle… »

Evidemment, nous devons chercher une borne plus universelle que les chères bornes gaussiennes de 68-95-99.7 (correspondant à une distance de 1/2/3 d’écart-type par rapport à la moyenne).

Par chance, il existe une telle limite appelée « limite de Chebyshev ».

Qu’est-ce que la limite de Chebyshev et en quoi est-elle utile ?

L’inégalité de Chebyshev (aussi appelée inégalité de Bienaymé-Chebyshev) garantit que, pour une large classe de distributions de probabilité, pas plus d’une certaine fraction de valeurs ne peuvent être à plus d’une certaine distance de la moyenne.

Spécifiquement, pas plus de 1/k² des valeurs de la distribution peuvent être éloignées de la moyenne de plus de k écarts-types (ou de manière équivalente, au moins 1-1/k² des valeurs de la distribution sont à moins de k écarts-types de la moyenne).

Elle s’applique à des types pratiquement illimités de distributions de probabilité et fonctionne sur une hypothèse beaucoup plus détendue que la normalité.

Comment fonctionne-t-elle ?

Même si vous ne savez rien du processus secret derrière vos données, il y a de bonnes chances que vous puissiez dire ce qui suit,

« Je suis sûr que 75% de toutes les données devraient tomber dans les 2 écarts types de la moyenne »,

Ou,

Je suis sûr que 89% de toutes les données devraient tomber dans les 3 écarts types de la moyenne ».

Voici à quoi cela ressemble pour une distribution d’apparence arbitraire,

Comment l’appliquer ?

Comme vous pouvez le deviner maintenant, la mécanique de base de votre analyse de données ne doit pas changer d’un iota. Vous allez toujours rassembler un échantillon des données (plus grand, mieux c’est), calculer les deux mêmes quantités que vous avez l’habitude de calculer – la moyenne et l’écart-type, puis appliquer les nouvelles limites au lieu de la règle 68-95-99,7.

Le tableau ressemble à ce qui suit (ici k désigne le nombre d’écarts types par rapport à la moyenne),

Une démonstration vidéo de son application est ici,

Quel est le piège ? Pourquoi les gens n’utilisent-ils pas cette borne « plus universelle » ?

Il est évident de savoir quel est le piège en regardant le tableau ou la définition mathématique. La règle de Chebyshev est beaucoup plus faible que la règle gaussienne en ce qui concerne la mise en place de limites sur les données.

Elle suit un modèle 1/k² par rapport à un modèle de chute exponentielle pour la distribution normale.

Par exemple, pour lier quoi que ce soit avec une confiance de 95%, vous devez inclure des données jusqu’à 4,5 écarts types contre. seulement 2 écarts types (pour la Normale).

Mais cela peut encore sauver la journée lorsque les données ne ressemblent en rien à une distribution Normale.

Y a-t-il quelque chose de mieux ?

Il existe une autre limite appelée, « Limite de Chernoff »/inégalité de Hoeffding qui donne une distribution à queue exponentiellement pointue (par rapport au 1/k²) pour les sommes de variables aléatoires indépendantes.

Ceci peut également être utilisé à la place de la distribution gaussienne lorsque les données ne semblent pas normales, mais seulement lorsque nous avons un haut degré de confiance dans le fait que le processus sous-jacent est composé de sous-processus qui sont complètement indépendants les uns des autres.

Malheureusement, dans de nombreux cas sociaux et commerciaux, les données finales sont le résultat d’une interaction extrêmement compliquée de nombreux sous-processus qui peuvent avoir une forte interdépendance.

Résumé

Dans cet article, nous avons appris un type particulier de limite statistique qui peut être appliqué à la plus large distribution possible de données indépendamment de l’hypothèse de normalité. Cela s’avère pratique lorsque nous savons très peu de choses sur la véritable source des données et que nous ne pouvons pas supposer qu’elles suivent une distribution gaussienne. La limite suit une loi de puissance au lieu d’une nature exponentielle (comme la gaussienne) et est donc plus faible. Mais c’est un outil important à avoir dans votre répertoire pour analyser n’importe quel type arbitraire de distribution de données.