Pourquoi 0,999… est égal à 1 ?!
On décembre 6, 2021 by adminUne autre façon de penser aux termes de notre sommation est que chaque terme successif est obtenu en multipliant le terme précédent par un rapport commun.
Cela signifie que nous avons une série géométrique qui converge vers a/(1 – r) où a est la première valeur de la série et r est le rapport par lequel nous multiplions pour obtenir le terme suivant.

La convergence dans une série signifie simplement que la série continuera à se rapprocher de plus en plus d’une valeur spécifique au fur et à mesure que vous ajoutez des termes à la série. La série se rapproche de manière infinitésimale de la valeur de convergence. Sur une échelle infinie, la convergence devient une égalité.
Dans notre cas, nous commençons par 1/10 et nous multiplions par 1/10 à chaque fois, donc a et r = 1/10.
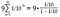
Complétez l’arithmétique du côté droit.

Nous avons maintenant formellement montré que 0.999… converge vers ou est égal à 1.
Pensées finales & Inspiration
Si cela vous semble étrange, c’est bien ! Vous savez que deux nombres différents, devraient en fait être des nombres différents. La nature contre-intuitive de ce problème est inhérente à l’étrangeté qui accompagne le travail avec l’infini.
Même dans un problème simple comme celui-ci, vous passez des limites de ce qui est tangible pour le cerveau humain à une échelle qui dépasse en quelque sorte notre compréhension. En tant qu’êtres finis, nous pouvons nous efforcer de comprendre le concept de l’infini ou de l’éternité, mais nous ne pouvons jamais en faire véritablement l’expérience. Ce qui signifie que souvent, ce que nous savons être vrai dans notre monde fini, s’avère se comporter différemment à un niveau infini.
Accepter la transition entre des mathématiques facilement découvrables et reproductibles et ce qui ne peut être que testé et imaginé dans notre esprit fait partie de la beauté et de l’émerveillement des mathématiques.
Ne prenez donc pas la leçon d’aujourd’hui au premier degré et haussez les épaules.
Laissez une couche de brouillard entre vous et la compréhension parfaite. Laissez votre esprit être soufflé par le fait que l’infini se comporte étrangement. Et laissez-le vous faire désirer plus de compréhension et surtout plus de mathématiques.
Merci de me lire et de réfléchir à l’infini avec moi aujourd’hui !
Laisser un commentaire