Fonctions ou cartographie

Maintenant, dans les fonctions ou cartographie, nous allons étudier un type spécial de relations appelées fonctions ou cartographie. Pour les comprendre, prenons quelques exemples concrets.

Toutes ces questions ont
des réponses uniques. Voyons
comment nous pouvons relier
ceci dans la cartographie de l’apprentissage.

● D’où le soleil se lève-t-il ?

Est

● Quelle est la capitale de l’Inde ?

Delhi

● Quel est le successeur de 4?

5

● Quelle est la somme de 5 et de 3 ?

8

Mappage ou fonctions:

Si A et B sont deux ensembles non vides, alors une relation ‘f’ de l’ensemble A à l’ensemble B est dite fonction ou mappage,
● Si chaque élément de l’ensemble A est associé à un élément unique de l’ensemble B.

● La fonction ‘f’ de A à B est notée f : A → B.

● Si f est une fonction de A vers B et que x ∈ A, alors f(x) ∈ B où f(x) est appelée l’image de x sous f et x est appelée la pré image de f(x) sous ‘f’.

Note:

Pour que f soit un mapping de A vers B:

● Chaque élément de A doit avoir une image dans B. La figure adjacente ne représente pas un mapping puisque l’élément d de l’ensemble A n’est associé à aucun élément de l’ensemble B.

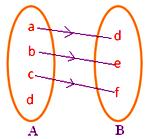
● Aucun élément de A ne doit avoir plus d’une image. La figure adjacente ne représente pas une mise en correspondance puisque l’élément b de l’ensemble A est associé à deux éléments d, f de l’ensemble B.

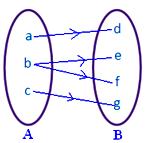
● Différents éléments de A peuvent avoir la même image dans B. La figure adjacente représente une cartographie.

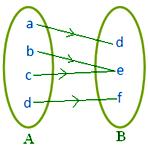
Note :

Toute cartographie est une relation mais toute relation peut ne pas être une cartographie.

Fonction comme un type spécial de relation:

Rappelons et passons en revue la fonction comme un type spécial de relation supposons, A et B sont deux ensembles non vides, alors une règle ‘f’ qui associe chaque élément de A à un élément unique de B est appelée une fonction ou un mapping de A à B.
Si ‘f’ est un mappage de A vers B,

on l’exprime par f : A → B

on le lit comme ‘f’ est une fonction de A vers B.
Si ‘f ‘ est une fonction de A vers B et x∈A et y∈B, alors on dit que y est l’image de l’élément x sous la fonction ‘ f ‘ et on le note par f(x).
On l’écrit donc y = f(x)

Ici, l’élément x est appelé la pré-image de y.

Ainsi, pour une fonction de A à B,
● A et B doivent être non vides.

● Chaque élément de A doit avoir une image dans B.

● Aucun élément de ‘A’ ne doit avoir plus d’une image dans ‘B’.
Note :

● Deux ou plusieurs éléments de A peuvent avoir la même image dans B.

● f : x → y signifie que sous la fonction de ‘f’ de A vers B, un élément x de A a une image y dans B.

● Il est nécessaire que chaque image de ‘f’ soit dans B mais il peut y avoir des éléments dans B qui ne sont pas des images de ‘f’ d’un élément de A.

● Relations et Mapping

Paire ordonnée

Produit cartésien de deux ensembles

Relation

Domaine et étendue d’une relation

Fonctions ou Mapping

Domaine co.domaine et l’étendue d’une fonction

● Relations et cartographie -. Feuilles de travail

Fiche de travail sur les relations mathématiques

Fiche de travail sur les fonctions ou la cartographie

.

Problèmes de mathématiques de 7e année

Pratique des mathématiques de 8e année
De Fonctions ou de Mappage à HOME PAGE

.