Circonférence d’un cercle – Explication et exemples

Nous avons vu précédemment comment trouver le périmètre du polygone. Nous savons que le cercle n’est pas un polygone, donc, il ne devrait pas avoir de périmètre. Nous utilisons une forme équivalente pour un cercle, appelée circonférence.

Dans cet article, nous allons discuter comment trouver la circonférence d’un cercle, la formule de la circonférence du cercle et des problèmes d’exemple sur la circonférence d’un cercle.

Qu’est-ce que la circonférence d’un cercle ?

La distance autour d’un polygone tel qu’un carré ou un rectangle est appelée le périmètre (P). En revanche, la distance autour d’un cercle est appelée la circonférence (C). Par conséquent, la circonférence d’un cercle est la distance linéaire d’un bord du cercle.

Pourquoi avons-nous besoin de calculer la circonférence d’un cercle ?

Déterminer la circonférence d’un objet est important dans les scénarios suivants :

Que vous vouliez acheter un soutien-gorge, un pantalon ou un pull, vous devez connaître la distance autour de votre taille ou de votre poitrine. Bien que votre corps ne soit pas un cercle parfait, vous devrez mesurer sa circonférence à l’aide d’un mètre ruban. Les tailleurs utilisent surtout cette technique pour déterminer la circonférence d’une robe.

Vous avez également besoin de connaître la circonférence d’un cercle en faisant des travaux d’artisanat, en installant une clôture autour de votre jacuzzi ou simplement en résolvant un problème de mathématiques pour l’école.

Comment trouver la circonférence d’un cercle ?

Comme indiqué précédemment, le périmètre ou la circonférence d’un cercle est la distance autour d’un cercle ou de toute forme circulaire. La circonférence d’un cercle est la même que la longueur d’une ligne droite qui est pliée ou courbée pour faire le cercle. La circonférence d’un cercle se mesure en mètres, kilomètres, yards, pouces, etc.

Il existe deux façons de trouver le périmètre ou la circonférence d’un cercle. La première formule implique l’utilisation du rayon et la seconde implique l’utilisation du diamètre d’un cercle. Il est important de noter que, les deux méthodes donnent le même résultat.

Permettons-nous de regarder.

La circonférence d’un cercle est donnée par ;

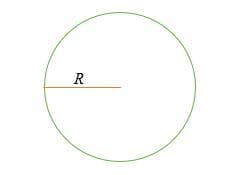
C = 2 * π* R = 2πR

où,

C = Circonférence ou périmètre,

R = le rayon d’un cercle,

π = la constante mathématique connue sous le nom de Pi

Or

C = π* D = π D

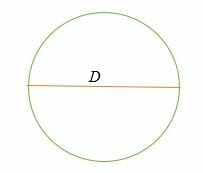
où, D = 2R = Le diamètre d’un cercle

Pour tout cercle, le rapport de sa circonférence à son diamètre est égal à une constante connue sous le nom de pi.

Circonférence/Diamètre = Pi

C /D = Pi ou C/2R = pi

La valeur approximative de pi (π) = 22/7 = 3,1415926535897….. (une valeur non terminale)

Pour faciliter le calcul de la circonférence d’un cercle, la valeur de pi est prise égale à 3,14 (π = 3,14).

Voyons quelques exemples ci-dessous pour polir le concept de circonférence.

Exemple 1

Trouver la circonférence du cercle dont le rayon est de 8 cm.

Solution

Circonférence = 2 * π* R = 2πR

= 2 * 3,14 * 8

= 50,24 cm.

Exemple 2

Calculez la circonférence d’un cercle dont le diamètre est de 70 mm

Solution

Circonférence = π* D = π D

= 3,14 * 70

= 219.8 mm

Exemple 3

Calculez le périmètre d’un jardin floral circulaire dont le rayon est de 10 m.

Solution

Circonférence = 2 * π* R = 2πR

= 2 * 3,14 * 10

= 62,8 m.

Exemple 4

La circonférence d’un cercle est de 440 mètres. Trouvez le diamètre et le rayon du cercle.

Solution

Circonférence = 2 * π* R = 2πR

440 =2 * 3,14 * R

440 = 6.28R

Divisez les deux côtés par 6,28 pour obtenir,

R = 70,06

Donc, le rayon du cercle est de 70,06 mètres. Mais, comme le diamètre est égal au double du rayon d’un cercle, alors, le diamètre est égal à 140,12 yards.

Exemple 5

Le diamètre des roues d’une bicyclette est de 100 cm. Combien de tours fera chaque roue pour parcourir une distance de 157 mètres

Solution

Calculer la circonférence de la roue de la bicyclette.

Circonférence = π D

= 3.14 * 100

= 314 cm

Pour obtenir le nombre de tours de la roue, divisez la distance parcourue par la circonférence de la roue.

Nous devons convertir 157 mètres en cm avant de diviser, donc nous multiplions 157 par 100 pour obtenir 15700 cm. Par conséquent,

Nombre de tours = 15700 cm/314 cm

= 50 tours.

Exemple 6

Un morceau de fil métallique en forme de rectangle de longueur 100 cm et de largeur 50 cm est coupé et plié pour former un cercle. Calculer la circonférence et le rayon du cercle formé.

Solution

La circonférence du cercle formé = le périmètre du fil rectangulaire.

Périmètre d’un rectangle = 2(L + W)

= 2(100 + 50) cm

= 2 * 150 cm

= 300 cm.

Par conséquent, la circonférence du cercle sera de 300 cm.

Mais calculez maintenant son rayon.

Circonférence = 2 π R

300 cm = 2 * π * R

300 cm = 2 * 3,14 * R

300 cm = 6,28R

Divisez les deux côtés par 6,28.

R = 47.77 cm

Donc, le rayon du cercle sera de 47,77 cm.

Exemple 7

Le rayon de chaque roue d’une motocyclette est de 0. 85 m. Quelle distance la motocyclette parcourra-t-elle si chaque roue effectue 1000 tours. Supposons que la motocyclette se déplace en ligne droite.

Solution

Premièrement, trouvez la circonférence de la roue.

Circonférence = 2 π R

= 2 * 3,14 * 0,85

= 5,338 m.

Pour trouver la distance parcourue, multipliez la circonférence de la roue par le nombre de tours effectués.

Distance = 5,338 * 1000

= 5338 m

Donc, la distance parcourue est égale à 5,338 kilomètres.

Questions pratiques

1. Une pizza de 12 pouces est servie à Mike et ses amis. Mike souhaite calculer sa circonférence. Aidez-le!
2. Le périmètre d’un carré particulier est 1/3 de l’aire d’un cercle particulier. Si la longueur du carré est de L unités, déterminez le diamètre du cercle en fonction de L.

Réponses

1. 12π pouces ou 37,67 pouces
2. 12L/π unités

La leçon précédente | Page principale | Leçon suivante

.