2.12 : Équation de Van der Waals

Une équation due à van der Waals étend l’équation du gaz idéal d’une manière directe. L’équation de Van der Waals est

\

Elle s’ajuste mieux aux données pression-volume-température d’un gaz réel que ne le fait l’équation du gaz idéal. L’ajustement amélioré est obtenu en introduisant deux paramètres (désignés par « \(a\) » et « \(b\) ») qui doivent être déterminés expérimentalement pour chaque gaz. L’équation de Van der Waals est particulièrement utile dans notre effort pour comprendre le comportement des gaz réels, car elle incarne une image physique simple de la différence entre un gaz réel et un gaz idéal.

En dérivant la loi de Boyle des lois de Newton, nous supposons que les molécules de gaz n’interagissent pas entre elles. Des arguments simples montrent que cela ne peut être qu’approximativement vrai. Les molécules de gaz réelles doivent interagir les unes avec les autres. À courte distance, elles se repoussent. À des distances un peu plus longues, elles s’attirent. L’équation du gaz idéal peut également être dérivée des hypothèses de base que nous avons formulées au §10 par une application de la théorie de la thermodynamique statistique. En faisant différentes hypothèses sur les propriétés des molécules, nous pouvons appliquer la thermodynamique statistique pour dériver l’équation de van der Waals ({}^{5}\). Les hypothèses requises sont que les molécules occupent un volume fini et qu’elles s’attirent mutuellement avec une force qui varie comme l’inverse d’une puissance de la distance qui les sépare. (On suppose habituellement que la force d’attraction est proportionnelle à \(r^{-6}\).)

Pour reconnaître que les molécules de gaz réelles s’attirent et se repoussent à la fois, il suffit de se rappeler que tout gaz peut être liquéfié en réduisant sa température et en augmentant la pression qui lui est appliquée. Si l’on refroidit davantage le liquide, il gèle et devient solide. Or, un solide se distingue par le fait qu’il conserve sa forme et qu’il est presque incompressible. Nous attribuons l’incompressibilité d’un solide aux forces répulsives entre les molécules qui le composent ; elles se sont tellement rapprochées les unes des autres que les forces répulsives entre elles sont devenues importantes. Pour comprimer le solide, il faut pousser les molécules encore plus près les unes des autres, ce qui nécessite une force démesurée. D’un autre côté, si nous jetons un glaçon à travers la pièce, toutes les molécules d’eau qui le composent volent ensemble à travers la pièce. De toute évidence, les molécules d’eau du solide sont attirées les unes par les autres, sinon elles partiraient toutes de leur côté – lancer le glaçon serait comme lancer une poignée de sable sec. Mais les molécules d’eau sont les mêmes molécules quelle que soit la température ou la pression, donc s’il existe des forces d’attraction et de répulsion entre elles dans le solide, ces forces doivent également être présentes dans les phases liquide et gazeuse.

Dans la phase gazeuse, les molécules sont éloignées les unes des autres ; dans la phase liquide ou solide, elles sont serrées les unes contre les autres. A son point d’ébullition, le volume d’un liquide est bien inférieur au volume du gaz à partir duquel il est condensé. Au point de congélation, le volume d’un solide n’est que légèrement différent du volume du liquide à partir duquel il est congelé, et il est certainement supérieur à zéro. Ces observations banales s’expliquent facilement en supposant que toute molécule a un volume caractéristique. Nous pouvons comprendre qu’il s’agit là d’une conséquence de la nature des forces intermoléculaires ; de toute évidence, ces forces deviennent plus fortes à mesure que la distance entre une paire de molécules diminue. Puisqu’un liquide ou un solide occupe un volume défini, la force répulsive doit augmenter plus rapidement que la force attractive lorsque la distance intermoléculaire est faible. Il est souvent utile de parler du volume molaire d’une phase condensée. Par volume molaire, on entend le volume d’une mole d’une substance pure. Le volume molaire d’une phase condensée est déterminé par la distance intermoléculaire à laquelle il y a un équilibre entre les forces intermoléculaires d’attraction et de répulsion.

Evidemment, les molécules sont très proches les unes des autres dans les phases condensées. Si l’on suppose que les espaces vides entre les molécules sont négligeables, le volume d’une phase condensée est approximativement égal au nombre de molécules dans l’échantillon multiplié par le volume d’une seule molécule. Le volume molaire est donc le nombre d’Avogadro multiplié par le volume occupé par une molécule. Si nous connaissons la densité, D, et la masse molaire, \(\overline{M}\), nous pouvons trouver le volume molaire, \(\overline{V}\), comme

\

Le volume occupé par une molécule, V\({}_{molécule}\), devient

\

La pression et le volume apparaissant dans l’équation de van der Waals sont la pression et le volume du gaz réel. Nous pouvons relier les termes de l’équation de van der Waals à l’équation du gaz idéal : Il est utile de considérer les termes \(\left(P+{{an}^2}/{V^2}\right)\) et \(\left(V-nb\right)\) comme la pression et le volume d’un gaz idéal hypothétique. C’est-à-dire

\N{4232>=nRT \end{align*}\]

Alors nous avons

\

Nous dérivons l’équation du gaz idéal d’un modèle dans lequel les molécules sont des masses ponctuelles sans interaction. Ainsi, le volume d’un gaz idéal est le volume occupé par un gaz dont les molécules individuelles ont un volume nul. Si les molécules individuelles d’un gaz réel occupent effectivement un volume \({b}/{\overline{N}}\), alors \(n\) moles d’entre elles occupent effectivement un volume

\

L’équation de Van der Waals dit que le volume d’un gaz réel est le volume qui serait occupé par des masses ponctuelles sans interaction, \(V_{ideal\ gas}\), plus le volume effectif des molécules de gaz elles-mêmes. (Lorsque les données relatives aux molécules de gaz réel sont ajustées à l’équation de van der Waals, la valeur de \(b\) est généralement un peu plus grande que le volume estimé à partir de la densité du liquide et de la masse moléculaire. Voir le problème 24.)

De façon similaire, on a

\

On peut comprendre cela comme une conséquence logique des interactions attractives entre les molécules du gaz réel. Avec \(a>0\), on dit que la pression du gaz réel est inférieure à la pression du gaz idéal hypothétique, d’une quantité qui est proportionnelle à \({\left({n}/{V}\right)}^2\). La constante de proportionnalité est \(a\). Comme \({n}/{V}\) est la densité molaire (nombre de moles par unité de volume) des molécules de gaz, il s’agit d’une mesure de la concentration. Le nombre de collisions entre molécules de même nature est proportionnel au carré de leur concentration. (Nous examinerons ce point plus en détail aux chapitres 4 et 5.) Ainsi, \({\gauche({n}/{V}\right)}^2\) est une mesure de la fréquence à laquelle les molécules de gaz réelles entrent en contact étroit les unes avec les autres. Si elles s’attirent lorsqu’elles sont proches les unes des autres, l’effet de cette attraction devrait être proportionnel à \({\left({n}/{V}\right)}^2\). L’équation de van der Waals est donc cohérente avec l’idée que la pression d’un gaz réel est différente de la pression du gaz idéal hypothétique d’une quantité qui est proportionnelle à la fréquence et à la force des interactions attractives.

Mais pourquoi les interactions attractives devraient-elles avoir cet effet ; pourquoi la pression du gaz réel devrait-elle être inférieure à celle du gaz idéal hypothétique ? La meilleure façon de développer une image qualitative est peut-être de reconnaître que les forces intermoléculaires attractives ont tendance à provoquer l’agglutination des molécules de gaz. Après tout, ce sont ces forces attractives qui font que les molécules s’agrègent en un liquide à basse température. Au-dessus du point d’ébullition, la capacité des molécules de gaz à se séparer limite les effets de cette tendance ; cependant, même dans le gaz, les forces d’attraction doivent agir d’une manière qui tend à réduire le volume occupé par les molécules. Comme le volume occupé par le gaz est dicté par la taille du récipient – et non par les propriétés du gaz lui-même – cette tendance à l’agglutination trouve son expression dans une diminution de la pression.

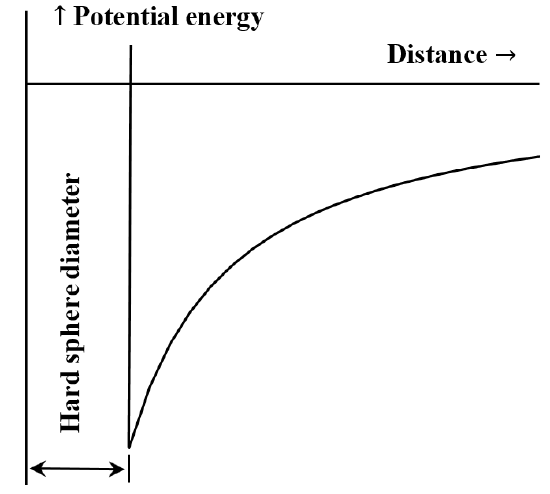
Il est souvent utile de décrire l’interaction entre des particules ou des fragments chimiques en termes de diagramme énergie potentielle/distance. L’équation de van der Waals correspond au cas où l’interaction répulsive entre les molécules est inexistante jusqu’à ce que les molécules entrent en contact. Une fois qu’elles sont en contact, l’énergie nécessaire pour les rapprocher encore devient arbitrairement grande. On décrit souvent ce phénomène en disant qu’elles se comportent comme des « sphères dures ». La force d’attraction entre deux molécules diminue à mesure que la distance qui les sépare augmente. Lorsqu’elles sont très éloignées l’une de l’autre, l’interaction attractive est très faible. On dit que l’énergie d’interaction est nulle lorsque les molécules sont infiniment éloignées. Si nous avons initialement deux molécules très éloignées, stationnaires et s’attirant mutuellement, elles se déplaceront spontanément l’une vers l’autre, en gagnant de l’énergie cinétique au fur et à mesure. Leur énergie potentielle diminue à mesure qu’elles se rapprochent l’une de l’autre, pour atteindre sa valeur la plus faible lorsque les molécules entrent en contact. Ainsi, l’équation de van der Waals implique le diagramme de l’énergie potentielle en fonction de la distance esquissé à la figure 5.

.