Ympyrän ympärysmitta – Selitys ja esimerkkejä

Katsoimme aiemmin, miten löydämme monikulmion ympärysmitan. Tiedämme, että ympyrä ei ole monikulmio, joten sillä ei pitäisi olla kehää. Käytämme ympyrälle vastaavaa muotoa, jota kutsutaan ympyrän ympärysmitaksi.

Tässä artikkelissa käsittelemme ympyrän ympärysmitan löytämistä, ympyrän ympärysmitan kaavaa ja esimerkkitehtäviä ympyrän ympärysmitasta.

Mikä on ympyrän ympärysmitta?

Matkaa monikulmion, kuten neliön tai suorakulmion, ympärysmitan ympärysmitta on nimeltään ympärysmitta (P). Toisaalta ympyrän ympärillä olevaa etäisyyttä kutsutaan kehäksi (C). Ympyrän ympärysmitta on siis ympyrän reunan lineaarinen etäisyys.

Miksi meidän täytyy laskea ympyrän ympärysmitta?

Kappaleen ympärysmitan määrittäminen on tärkeää seuraavissa tilanteissa:

Oletpa sitten ostamassa rintaliivejä, housuja tai villapaitaa, sinun täytyy tietää etäisyys vyötäröltä tai rinnalta. Vaikka vartalosi ei ole täydellinen ympyrä, sinun on mitattava sen ympärysmitta mittanauhan avulla. Räätälit käyttävät tätä tekniikkaa useimmiten mekon ympärysmitan määrittämiseen.

Tarvitset ympyrän ympärysmitan myös tehdessäsi askartelutöitä, laittaessasi aidan poreammeen ympärille tai ratkaistessasi matemaattista tehtävää koulua varten.

Miten ympyrän ympärysmitta saadaan selville?

Kuten edellä on todettu, ympyrän ympärysmitta tai ympyrän ympärysmitta on matkan pituus ympyrän tai minkä tahansa ympyränmuotoisen kappaleen ympärillä. Ympyrän kehä on sama kuin sellaisen suoran pituus, joka on taitettu tai taivutettu ympyrän muodostamiseksi. Ympyrän ympärysmitta mitataan metreinä, kilometreinä, jaardeina, tuumina jne.

Ympyrän ympärysmitta tai kehä voidaan määrittää kahdella tavalla. Ensimmäisessä kaavassa käytetään sädettä ja toisessa ympyrän halkaisijaa. On tärkeää huomata, että molemmilla menetelmillä saadaan sama tulos.

Katsotaanpa.

Ympyrän kehä saadaan kaavalla;

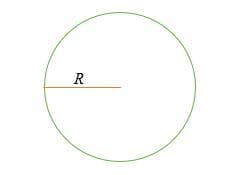
C = 2 * π* R = 2πR

jossa,

C = ympyrän ympärysmitta tai kehä,

R = ympyrän säde,

π = matemaattinen vakio, joka tunnetaan nimellä Pi

Or

C = π* D = π D

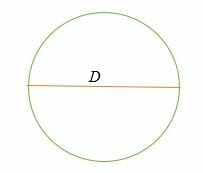
missä,D = 2R = ympyrän halkaisija

Mille tahansa ympyrälle sen kehän ja halkaisijan suhde on yhtä suuri kuin vakio, joka tunnetaan nimellä pi.

Ympärysmitta/halkaisija = Pi

C /D = Pi tai C/2R = pi

Piin (π) likimääräinen arvo = 22/7 = 3.1415926535897….. (päättymätön arvo)

Ympyrän kehän laskemisen helpottamiseksi pi:n arvoksi otetaan 3,14 (π = 3,14).

Katsotaan alla muutama esimerkki kehän käsitteen hiomiseksi.

Esimerkki 1

Etsitään ympyrän ympärysmitta, jonka säde on 8 cm.

Ratkaisu

Ympärysmitta = 2 * π* R = 2πR

= 2 * 3,14 * 8

= 50,24 cm.

Esimerkki 2

Lasketaan sellaisen ympyrän ympärysmitta, jonka halkaisija on 70 mm

Ratkaisu

Ympärysmitta = π* D = π D

= 3.14 * 70

= 219.8 mm

Esimerkki 3

Lasketaan pyöreän kukkapuutarhan ympärysmitta, jonka säde on 10 m.

Ratkaisu

Ympärysmitta = 2 * π* R = 2πR

= 2 * 3.14 * 10

= 62.8 m.

Esimerkki 4

Ympyrän ympärysmitta on 440 metriä. Etsi ympyrän halkaisija ja säde.

Ratkaisu

Ympärysmitta = 2 * π* R = 2πR

440 =2 * 3.14 * R

440 = 6.28R

Jakaen molemmat puolet luvulla 6,28 saadaan,

R = 70,06

Ympyrän säde on siis 70,06 metriä. Mutta koska halkaisija on kaksi kertaa ympyrän säde, niin halkaisija on 140,12 jaardia.

Esimerkki 5

Pyörän pyörien halkaisija on 100 cm. Kuinka monta kierrosta kukin pyörä tekee kulkeakseen 157 metrin matkan

Ratkaisu

Lasketaan polkupyörän pyörän ympärysmitta.

Ympärysmitta = π D

= 3.14 * 100

= 314 cm

Pyörän kierrosluvun saamiseksi jaetaan kuljettu matka pyörän ympärysmitalla.

Meidän on muunnettava 157 metriä senttimetreiksi ennen jakamista, joten kerromme 157:llä 100:lla, jolloin saadaan 15700 cm. Näin ollen,

Kierrosten määrä = 15700 cm/314 cm

= 50 kierrosta.

Esimerkki 6

Langanpätkä, joka on suorakulmion muotoinen, jonka pituus on 100 cm ja leveys 50 cm, leikataan ja taitetaan ympyräksi. Laske muodostetun ympyrän kehä ja säde.

Ratkaisu

Muodostetun ympyrän kehä = suorakulmaisen langan kehä.

Suorakulmion ympärysmitta = 2(L + S)

= 2(100 + 50) cm

= 2 * 150 cm

= 300 cm.

Ympyrän ympärysmitta on siis 300 cm.

Lasketaan nyt sen säde.

Ympäryspiiri = 2 π R

300 cm = 2 * π * R

300 cm = 2 * 3,14 * R

300 cm = 6,28R

Jaa molemmat puolet luvulla 6,28.

R = 47.77 cm

Ympyrän säde on siis 47,77 cm.

Esimerkki 7

Moottoripyörän jokaisen pyörän säde on 0. 85 m. Kuinka kauas moottoripyörä liikkuu, jos jokainen pyörä ottaa 1000 kierrosta. Oletetaan, että moottoripyörä liikkuu suoraviivaisesti.

Ratkaisu

Löydetään ensin pyörän ympärysmitta.

Ympärysmitta = 2 π R

= 2 * 3,14 * 0,85

= 5,338 m.

Löytääksemme kuljetun matkan kerromme pyörän ympärysmitan otettujen kierrosten lukumäärällä.

Matka = 5,338 * 1000

= 5338 m

Siten kuljettu matka on 5,338 kilometriä.

Käytännön kysymyksiä

1. Mikelle ja hänen ystävilleen tarjoillaan 12-tuumainen pizza. Mike on kiinnostunut laskemaan sen ympärysmitan. Auta häntä!
2. Tämän tietyn neliön ympärysmitta on 1/3 tietyn ympyrän pinta-alasta. Jos neliön pituus on L yksikköä, määritä ympyrän halkaisija L:n suhteen.

Vastaukset

1. 12π tuumaa tai 37.67 tuumaa
2. 12L/π yksikköä

Edellinen oppitunti | Pääsivu | Seuraava oppitunti