Tutkimusmenetelmät psykologiassa

Mitä on korrelaatiotutkimus?

Korrelaatiotutkimus on eräänlainen ei-kokeellinen tutkimustyyppi, jossa tutkija mittaa kahta muuttujaa (binääristä tai jatkuvaa) ja arvioi tilastollista suhdetta (ts., korrelaatio) niiden välillä pyrkien vain vähän tai ei lainkaan kontrolloimaan ulkopuolisia muuttujia. On monia syitä, joiden vuoksi muuttujien välisistä tilastollisista suhteista kiinnostuneet tutkijat valitsevat korrelaatiotutkimuksen kokeen sijasta. Ensimmäinen on se, että he eivät usko, että tilastollinen suhde on kausaalinen, tai he eivät ole kiinnostuneita kausaalisista suhteista. Muistutettakoon, että tieteen kaksi tavoitetta ovat kuvaaminen ja ennustaminen, ja korrelaatiotutkimusstrategian avulla tutkijat voivat saavuttaa molemmat tavoitteet. Erityisesti tätä strategiaa voidaan käyttää kuvaamaan kahden muuttujan välisen suhteen voimakkuutta ja suuntaa, ja jos muuttujien välillä on suhde, tutkijat voivat käyttää yhden muuttujan pistemääriä ennustamaan toisen muuttujan pistemääriä (käyttämällä tilastollista tekniikkaa, jota kutsutaan regressioksi ja jota käsitellään tarkemmin tämän luvun kompleksista korrelaatiota käsittelevässä jaksossa).

Toinen syy siihen, että tutkijat valitsevat korrelaatiotutkimuksen kokeen sijasta, on se, että kiinnostavan tilastollisen suhteen ajatellaan olevan kausaalinen, mutta tutkija ei voi manipuloida riippumatonta muuttujaa, koska se on mahdotonta, epäkäytännöllistä tai epäeettistä. Vaikka tutkija voisi esimerkiksi olla kiinnostunut kannabiksen käyttötiheyden ja muistikyvyn välisestä suhteesta, hän ei voi eettisesti manipuloida kannabiksen käyttötiheyttä. Näin ollen hänen on turvauduttava korrelaatiotutkimusstrategiaan; hänen on yksinkertaisesti mitattava kannabiksen käyttötiheys ja mitattava ihmisten muistikyky standardoidulla muistitestillä ja määritettävä sitten, onko kannabiksen käyttötiheys tilastollisesti yhteydessä muistitestisuoritukseen.

Korrelaatiota käytetään myös mittausten luotettavuuden ja pätevyyden selvittämiseen. Tutkija voi esimerkiksi arvioida lyhyen ekstraversiotestin pätevyyttä antamalla sen suurelle osallistujajoukolle yhdessä pidemmän ekstraversiotestin kanssa, joka on jo osoitettu päteväksi. Tutkija voisi sitten tarkistaa, korreloivatko osallistujien lyhyestä testistä saamat pisteet vahvasti pidemmästä testistä saatujen pisteiden kanssa. Kummankaan testituloksen ei uskota aiheuttavan toista, joten manipuloitavaa riippumatonta muuttujaa ei ole. Itse asiassa termit riippumaton muuttuja ja riippuvainen muuttuja eivät päde tämäntyyppiseen tutkimukseen.

Korrelaatiotutkimuksen vahvuutena on myös se, että sen ulkoinen validiteetti on usein korkeampi kuin kokeellisen tutkimuksen. Muistutettakoon, että sisäisen validiteetin ja ulkoisen validiteetin välillä on yleensä kompromissi. Kun kokeisiin lisätään enemmän kontrolleja, sisäinen validiteetti lisääntyy, mutta usein ulkoisen validiteetin kustannuksella, koska käyttöön otetaan keinotekoisia olosuhteita, joita ei todellisuudessa ole. Sitä vastoin korrelaatiotutkimusten sisäinen validiteetti on tyypillisesti alhainen, koska mitään ei manipuloida tai valvota, mutta niiden ulkoinen validiteetti on usein korkea. Koska kokeen tekijä ei manipuloi tai kontrolloi mitään, tulokset heijastavat todennäköisemmin reaalimaailmassa vallitsevia suhteita.

Tämän sisäisen ja ulkoisen validiteetin välisen kompromissin jatkeeksi korrelaatiotutkimus voi auttaa tuottamaan yhtenevää näyttöä teorian tueksi. Jos teoriaa tukee todellinen koe, jonka sisäinen validiteetti on korkea, sekä korrelaatiotutkimus, jonka ulkoinen validiteetti on korkea, tutkijat voivat luottaa enemmän teoriansa pätevyyteen. Konkreettisena esimerkkinä voidaan todeta, että korrelaatiotutkimuksia, joissa todetaan, että väkivaltaisen television katselun ja aggressiivisen käyttäytymisen välillä on yhteys, on täydennetty kokeellisilla tutkimuksilla, jotka vahvistavat, että yhteys on kausaalinen (Bushman & Huesmann, 2001).

Onko korrelaatiotutkimuksessa aina mukana kvantitatiivisia muuttujia?

Aloittelevien tutkijoiden yleinen harhaluulo on, että korrelaatiotutkimuksessa on oltava mukana kaksi kvantitatiivista muuttujaa, kuten kahden ekstraversiotestin pisteet tai ihmisten kokema päivittäisten hässäköiden ja oireiden määrä. Korrelaatiotutkimuksen ominaispiirre on kuitenkin se, että kahta muuttujaa mitataan – kumpaakaan ei manipuloida – ja tämä pätee riippumatta siitä, ovatko muuttujat määrällisiä vai kategorisia. Kuvitellaan esimerkiksi, että tutkija antaa Rosenbergin itsetuntoasteikon 50 amerikkalaiselle ja 50 japanilaiselle yliopisto-opiskelijalle. Vaikka tämä ”tuntuu” koehenkilöiden väliseltä kokeelta, kyseessä on korrelaatiotutkimus, koska tutkija ei ole manipuloinut opiskelijoiden kansallisuuksia. Sama pätee Cacioppon ja Pettyn tutkimukseen, jossa verrataan yliopistojen opettajakuntaa ja tehdastyöläisiä heidän kognition tarpeensa suhteen. Kyseessä on korrelaatiotutkimus, koska tutkijat eivät manipuloineet osallistujien ammatteja.

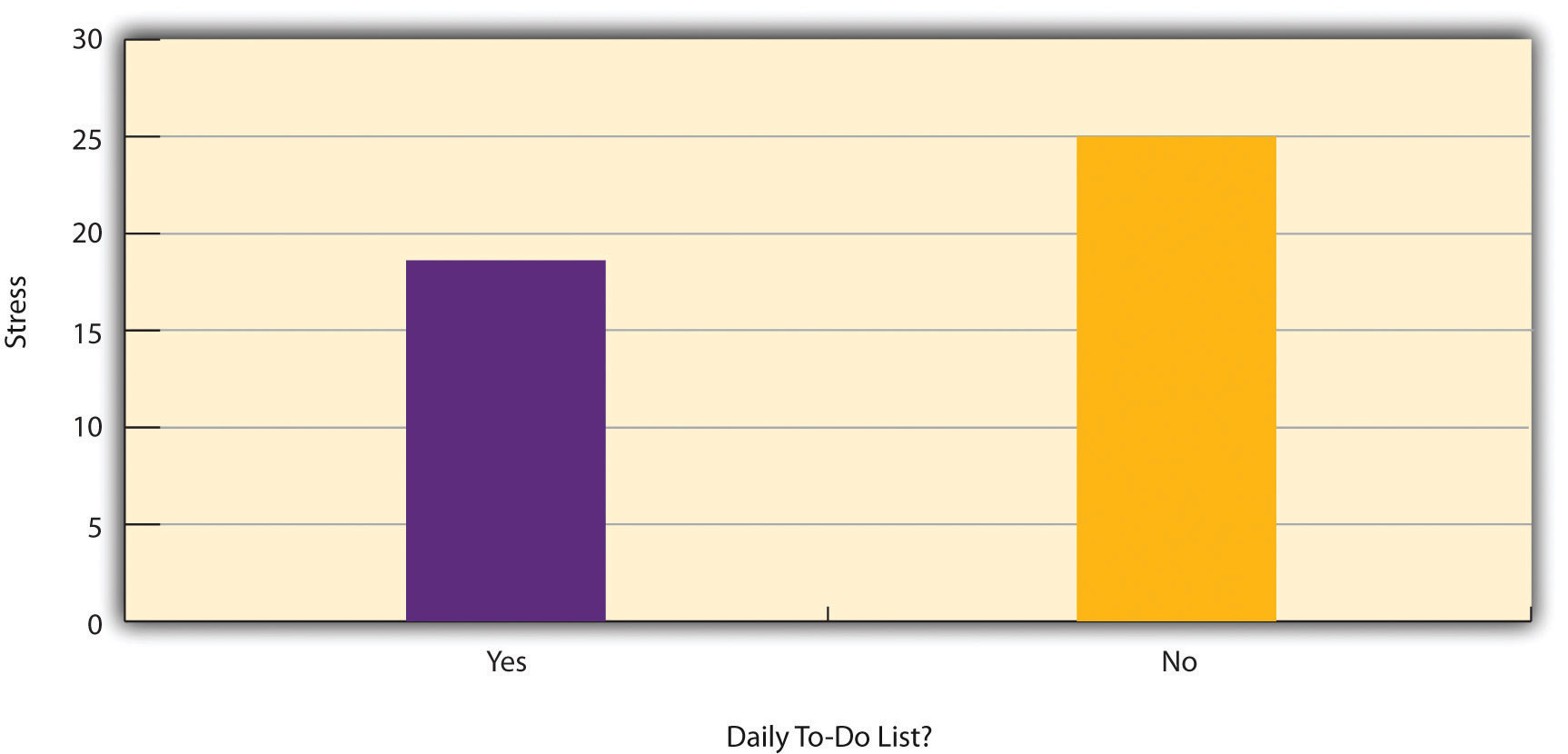
Kuviossa 6.2 on tietoja hypoteettisesta tutkimuksesta, jossa selvitetään, onko ihmisillä yhteys sen välillä, tekevätkö he päivittäin listan tehtävistä asioista (”tehtävälista”), ja stressin välillä. Huomaa, että on epäselvää, onko kyseessä koe vai korrelaatiotutkimus, koska on epäselvää, onko riippumatonta muuttujaa manipuloitu. Jos tutkija määräsi satunnaisesti osan osallistujista tekemään päivittäisiä tehtävälistoja ja osan ei, kyseessä on koe. Jos tutkija vain kysyi osallistujilta, tekivätkö he päivittäin tehtävälistoja, kyseessä on korrelaatiotutkimus. Erottelu on tärkeää, koska jos tutkimus olisi koe, voitaisiin päätellä, että päivittäisten tehtävälistojen tekeminen vähensi osallistujien stressiä. Mutta jos kyseessä olisi korrelaatiotutkimus, voitaisiin vain päätellä, että nämä muuttujat ovat tilastollisesti yhteydessä toisiinsa. Ehkä stressillä on kielteinen vaikutus ihmisten kykyyn suunnitella eteenpäin (suuntaavuusongelma). Tai ehkä ihmiset, jotka ovat tunnollisempia, tekevät todennäköisemmin tehtävälistoja ja ovat harvemmin stressaantuneita (kolmannen muuttujan ongelma). Ratkaisevaa on, että se, mikä määrittelee tutkimuksen kokeelliseksi tai korrelatiiviseksi, ei ole tutkittavat muuttujat, se, ovatko muuttujat kvantitatiivisia vai kategorisia, eikä se, minkälaista kuvaajaa tai tilastoa käytetään tietojen analysointiin. Tutkimuksen määrittelee se, miten tutkimus suoritetaan.

Tiedonkeruu korrelaatiotutkimuksessa

Korrelaatiotutkimuksen määrittelevänä piirteenä on jälleen se, että kumpaankaan muuttujaan ei ole vaikutettu. Sillä ei ole merkitystä, miten tai missä muuttujat mitataan. Tutkija voi pyytää osallistujia tulemaan laboratorioon suorittamaan tietokonepohjaisen taaksepäin suuntautuvan numerosarjatehtävän ja tietokonepohjaisen riskipäätöksentekotehtävän ja arvioida sitten osallistujien näistä kahdesta tehtävästä saamien pisteiden välistä suhdetta. Tai tutkija voi mennä ostoskeskukseen ja kysyä ihmisiltä heidän asenteistaan ympäristöä kohtaan ja heidän ostotottumuksistaan ja arvioida sitten näiden kahden muuttujan välistä suhdetta. Molemmat näistä tutkimuksista olisivat korrelaatiotutkimuksia, koska mitään riippumatonta muuttujaa ei manipuloida.

Kvantitatiivisten muuttujien väliset korrelaatiot

Kvantitatiivisten muuttujien väliset korrelaatiot esitetään usein hajontakuvioiden avulla. Kuvassa 6.3 esitetään joitakin hypoteettisia tietoja ihmisten stressin määrän ja heidän fyysisten oireidensa määrän välisestä suhteesta. Jokainen piste hajontakuviossa edustaa yhden henkilön pistemäärää molemmissa muuttujissa. Esimerkiksi ympyröity piste kuvassa 6.3 edustaa henkilöä, jonka stressipisteet olivat 10 ja jolla oli kolme fyysistä oiretta. Kun kaikki pisteet otetaan huomioon, voidaan nähdä, että henkilöillä, joilla on enemmän stressiä, on yleensä enemmän fyysisiä oireita. Tämä on hyvä esimerkki positiivisesta suhteesta, jossa korkeammat pisteet yhdessä muuttujassa ovat yleensä yhteydessä korkeampiin pisteisiin toisessa muuttujassa. Toisin sanoen ne liikkuvat samaan suuntaan, joko molemmat ylöspäin tai molemmat alaspäin. Negatiivinen suhde on sellainen, jossa korkeammat pistemäärät yhdessä muuttujassa ovat yleensä yhteydessä matalampiin pistemääriin toisessa muuttujassa. Toisin sanoen ne liikkuvat vastakkaisiin suuntiin. Esimerkiksi stressin ja immuunijärjestelmän toiminnan välillä on negatiivinen suhde, koska korkeampi stressi on yhteydessä matalampaan immuunijärjestelmän toimintaan.

Kvantitatiivisten muuttujien välisen korrelaation voimakkuutta mitataan tavallisesti tilastolla nimeltä Pearsonin korrelaatiokerroin (tai Pearsonin r). Kuten kuvasta 6.4 käy ilmi, Pearsonin r vaihtelee välillä -1,00 (vahvin mahdollinen negatiivinen suhde) ja +1,00 (vahvin mahdollinen positiivinen suhde). Arvo 0 tarkoittaa, että kahden muuttujan välillä ei ole yhteyttä. Kun Pearsonin r on 0, hajontakuvion pisteet muodostavat muodottoman ”pilven”. Kun sen arvo siirtyy kohti -1,00 tai +1,00, pisteet osuvat yhä lähempänä yhtä suoraa viivaa. Korrelaatiokertoimia, jotka ovat lähellä ±.10, pidetään pieninä, arvoja, jotka ovat lähellä ±.30, pidetään keskisuurina ja arvoja, jotka ovat lähellä ±.50, pidetään suurina. Huomaa, että Pearsonin r:n merkki ei liity sen voimakkuuteen. Esimerkiksi Pearsonin r-arvot +,30 ja -,30 ovat yhtä vahvoja; toinen edustaa vain kohtalaisen positiivista suhdetta ja toinen kohtalaisen negatiivista suhdetta. Luotettavuuskertoimia lukuun ottamatta useimmat psykologiassa esiintyvät korrelaatiot ovat kooltaan pieniä tai kohtalaisia. Kristoffer Magnussonin luoma verkkosivusto http://rpsychologist.com/d3/correlation/ tarjoaa erinomaisen interaktiivisen korrelaatioiden visualisoinnin, jonka avulla voit säätää korrelaation voimakkuutta ja suuntaa ja samalla todistaa vastaavat muutokset hajontakuvassa.

On kaksi yleistä tilannetta, joissa Pearsonin r:n arvo voi olla harhaanjohtava. Pearsonin r on hyvä mittari vain lineaarisille suhteille, joissa pisteitä approksimoi parhaiten suora viiva. Se ei ole hyvä mittari epälineaarisille suhteille, joissa pisteitä lähestyy paremmin kaareva viiva. Kuviossa 6.5 esitetään esimerkiksi hypoteettinen yhteys ihmisten yöunien määrän ja heidän masennustasonsa välillä. Tässä esimerkissä pisteitä parhaiten kuvaava viiva on käyrä – eräänlainen ylösalaisin oleva ”U” – koska ihmiset, jotka nukkuvat noin kahdeksan tuntia, ovat yleensä vähiten masentuneita. Ne, jotka nukkuvat liian vähän ja ne, jotka nukkuvat liikaa, ovat yleensä masentuneempia. Vaikka kuvio 6.5 osoittaa melko vahvan yhteyden masennuksen ja unen välillä, Pearsonin r olisi lähellä nollaa, koska hajontakuvion pisteet eivät sovi hyvin yhteen suoraan. Tämä tarkoittaa, että on tärkeää tehdä hajontakuvio ja varmistaa, että suhde on suunnilleen lineaarinen, ennen kuin käytetään Pearsonin r:ää. Epälineaariset suhteet ovat melko yleisiä psykologiassa, mutta niiden voimakkuuden mittaaminen ei kuulu tämän kirjan piiriin.

Toinen yleinen tilanne, jossa Pearsonin r:n arvo voi olla harhaanjohtava, on silloin, kun jommankumman tai molempien muuttujien vaihteluväli on otoksessa rajallinen suhteessa perusjoukkoon. Tätä ongelmaa kutsutaan vaihteluvälin rajoittamiseksi. Oletetaan esimerkiksi, että ihmisten iän ja heidän hip hop -musiikista nauttimisensa välillä on voimakas negatiivinen korrelaatio, kuten kuvan 6.6 hajontakuvio osoittaa. Pearsonin r on tässä tapauksessa -,77. Jos kuitenkin kerättäisiin tietoja vain 18-24-vuotiailta, joita kuvion 6.6 tummennettu alue edustaa, yhteys näyttäisi olevan melko heikko. Itse asiassa Pearsonin r tällä rajoitetulla ikäalueella on 0. Siksi on hyvä ajatus suunnitella tutkimukset siten, että vältetään alueen rajoittaminen. Jos esimerkiksi ikä on yksi ensisijaisista muuttujista, voit suunnitella kerääväsi tietoja monen ikäisiltä ihmisiltä. Koska vaihteluvälin rajoittuminen ei aina ole ennakoitavissa tai helposti vältettävissä, on kuitenkin hyvä käytäntö tutkia aineistosi mahdollisen vaihteluvälin rajoittumisen varalta ja tulkita Pearsonin r-arvoa sen valossa. (On olemassa myös tilastollisia menetelmiä Pearsonin r:n korjaamiseksi vaihteluvälin rajoittumisen vuoksi, mutta ne eivät kuulu tämän kirjan aihepiiriin.)

Korrelaatio ei merkitse kausaalisuutta

Olet luultavasti kuullut toistuvasti, että ”korrelaatio ei merkitse kausaalisuutta”. Huvittava esimerkki tästä tulee vuonna 2012 tehdystä tutkimuksesta, joka osoitti positiivisen korrelaation (Pearsonin r = 0,79) kansakunnan suklaan kulutuksen henkeä kohti ja kyseisen kansakunnan kansalaisille myönnettyjen Nobel-palkintojen määrän välillä. Vaikuttaa kuitenkin selvältä, että tämä ei tarkoita sitä, että suklaan syöminen aiheuttaa sen, että ihmiset voittavat Nobel-palkintoja, eikä olisi järkevää yrittää lisätä voitettujen Nobel-palkintojen määrää suosittelemalla, että vanhemmat syöttäisivät lapsilleen enemmän suklaata.

On kaksi syytä siihen, että korrelaatio ei merkitse syy-yhteyttä. Ensimmäistä kutsutaan suuntaavuusongelmaksi. Kaksi muuttujaa, X ja Y, voivat olla tilastollisesti yhteydessä toisiinsa joko siksi, että X aiheuttaa Y:n, tai siksi, että Y aiheuttaa X:n. Ajatellaan esimerkiksi tutkimusta, joka osoittaa, että se, harrastavatko ihmiset liikuntaa vai eivät, on tilastollisesti yhteydessä siihen, kuinka onnellisia he ovat – siten, että ihmiset, jotka harrastavat liikuntaa, ovat keskimäärin onnellisempia kuin ihmiset, jotka eivät harrasta liikuntaa. Tämä tilastollinen yhteys on johdonmukainen sen ajatuksen kanssa, että liikunta aiheuttaa onnellisuutta, mutta se on johdonmukainen myös sen ajatuksen kanssa, että onnellisuus aiheuttaa liikuntaa. Ehkä onnellisuus antaa ihmisille enemmän energiaa tai saa heidät etsimään mahdollisuuksia seurustella muiden kanssa käymällä kuntosalilla. Toista syytä siihen, että korrelaatio ei merkitse syy-yhteyttä, kutsutaan kolmannen muuttujan ongelmaksi. Kaksi muuttujaa, X ja Y, voivat olla tilastollisesti yhteydessä toisiinsa, ei siksi, että X aiheuttaa Y:n tai Y aiheuttaa X:n, vaan siksi, että jokin kolmas muuttuja, Z, aiheuttaa sekä X:n että Y:n. Esimerkiksi se, että Nobel-palkintoja enemmän voittaneilla kansakunnilla on taipumus syödä enemmän suklaata, heijastelee luultavasti maantieteellistä tilannetta, sillä Euroopan maissa on taipumus syödä enemmän suklaata henkeä kohti ja investoida enemmän koulutukseen ja tekniikkaan (jälleen kerran henkeä kohti) kuin monissa muissa maailman maissa. Vastaavasti liikunnan ja onnellisuuden välinen tilastollinen yhteys voi tarkoittaa, että jokin kolmas muuttuja, kuten fyysinen terveys, aiheuttaa molemmat muuttujat. Fyysisesti terveenä oleminen voisi saada ihmiset harrastamaan liikuntaa ja saada heidät olemaan onnellisempia. Korrelaatioita, jotka johtuvat kolmannesta muuttujasta, kutsutaan usein vääristyneiksi korrelaatioiksi.

Erinomaisia ja huvittavia esimerkkejä vääristyneistä korrelaatioista löytyy osoitteesta http://www.tylervigen.com (kuvassa 6.7 on yksi tällainen esimerkki).

.