Mitä jos datasi EI ole normaalia?

Esittely

Tänään on halloween-viikko, ja temppujen ja herkkujen välissä me datanörtit naureskelemme sosiaalisessa mediassa tälle söpölle meemille.

Luuletko tämän olevan vitsi? Minäpä kerron teille, että tämä ei ole naurun asia. Se on pelottavaa, Halloweenin hengen mukaisesti!

Jos emme voi olettaa, että suurin osa tiedoistamme (liiketaloudellisesta, yhteiskunnallisesta, taloudellisesta tai tieteellisestä alkuperästä) on ainakin likimain ”Normaalia” (eli ne syntyvät Gaussin prosessin tai useiden tällaisten prosessien summan tuloksena), olemme tuhoon tuomittuja!

Tässä on äärimmäisen lyhyt lista asioista, jotka eivät kelpaa,

• Koko kuuden sigman käsite
• Kuuluisa 68-95-99.7-sääntö
• ’Pyhä’ käsite p=0.05 (tulee 2 sigman väleistä) tilastollisessa analyysissä

Kyllä tarpeeksi pelottavaa? Puhutaanpa siitä lisää…

Kaikkivoipa ja kaikkivoipa normaalijakauma

Pidetään tämä osio lyhyenä ja ytimekkäänä.

Normaalijakauma (Gaussin jakauma) on laajimmin tunnettu todennäköisyysjakauma. Tässä muutamia linkkejä sen voimaa ja laajaa sovellettavuutta kuvaaviin artikkeleihin,

• Miksi datatieteilijät rakastavat Gaussia

• How to Dominate the Statistics Portion of Your Data Science Interview
• What’s So Important about the Normal Distribution?

Johtuen sen esiintymisestä eri aloilla ja Central Limit Theoremista (CLT), tämä jakauma on keskeisellä sijalla datatieteessä ja analytiikassa.

Mikä sitten on ongelma?

Tämä kaikki on hunky-dory, mikä on ongelma?

Ongelma on se, että usein saatat löytää tietylle data-aineistollesi jakauman, joka ei välttämättä täytä normaalisuutta eli normaalijakauman ominaisuuksia. Mutta koska oletus normaalijakaumasta on liian riippuvainen, useimmat liiketoiminta-analytiikan kehykset on räätälöity työskentelemään normaalijakautuneiden datajoukkojen kanssa.

Se on melkein juurtunut alitajuntaamme.

Esitettäköön, että sinua pyydetään havaitsemaan, tarkistetaanko jostain prosessista (insinööritieteestä tai liiketaloudellisesta toiminnasta) peräisin olevan uuden datan erä järkeväksi. ’Järkevyydellä’ tarkoitat sitä, kuuluuko uusi data eli onko se ’odotetun vaihteluvälin’ sisällä.

Mikä on tämä ’odotus’? Miten vaihteluväli kvantifioidaan?

Automaattisesti, ikään kuin alitajunnan ohjaamana, mittaamme näytetietoaineiston keskiarvon ja keskihajonnan ja siirrymme tarkistamaan, kuuluuko uusi tieto tietyn keskihajonnan vaihteluvälin sisälle.

Jos joudumme työskentelemään 95 %:n luottamusrajalla, olemme tyytyväisiä nähdessämme, että tieto on kahden keskihajonnan sisällä. Jos tarvitsemme tiukemman rajan, tarkistamme 3 tai 4 keskihajontaa. Laskemme Cpk:n tai noudatamme kuuden sigman ohjeita ppm (parts-per-million) -laatutasoa varten.

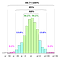
Kaikkien näiden laskelmien lähtökohtana on implisiittinen oletus siitä, että populaatiodata (EI siis otos) noudattaa Gaussin jakaumaa i.ts. perusprosessia, josta kaikki data on syntynyt (menneisyydessä ja nykyhetkessä), hallitsee vasemmanpuoleinen kuvio.

Mutta mitä tapahtuu, jos data noudattaa oikealla puolella olevaa kuviota?

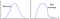
Vai tätä ja… sitä?

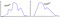
Onko olemassa yleispätevämpi luottamusraja, kun aineisto EI ole normaali?

Loppujen lopuksi tarvitsemme silti matemaattisesti järkevän tekniikan luottamusrajan kvantifioimiseksi, vaikka aineisto ei olisi normaalia. Tämä tarkoittaa, että laskelmamme voi muuttua hieman, mutta meidän pitäisi silti pystyä sanomaan jotakin tällaista-

”Todennäköisyys havaita uusi datapiste tietyllä etäisyydellä keskiarvosta on tällainen ja tällainen…”

On ilmeistä, että meidän on etsittävä yleispätevämpää rajaa kuin vaalitut Gaussin rajat 68-95-99.7 (joka vastaa 1/2/3 standardipoikkeaman etäisyyttä keskiarvosta).

Onneksi on olemassa yksi tällainen raja nimeltä ”Chebyshev Bound”.

Mikä on Chebyshev Bound ja miten se on hyödyllinen?

Chebyshevin epätasa-arvo (jota kutsutaan myös Bienaymé-Chebyshev-epätasa-arvoksi) takaa, että laajalle todennäköisyysjakaumien luokalle enintään tietty murto-osa arvoista voi olla yli tietyn etäisyyden päässä keskiarvosta.

Kohtaisesti, enintään 1/k² jakauman arvoista voi olla yli k keskihajonnan päässä keskiarvosta (tai vastaavasti vähintään 1-1/k² jakauman arvoista on k keskihajonnan sisällä keskiarvosta).

Se soveltuu käytännössä rajoittamattomiin todennäköisyysjakaumatyyppeihin ja toimii paljon väljemmällä oletuksella kuin normaalisuus.

Miten se toimii?

Vaikka et tietäisikään mitään datasi taustalla olevasta salaisesta prosessista, on hyvin mahdollista, että voit sanoa seuraavaa,

”Olen varma, että 75 %:n kaikesta datasta pitäisi osua 2 keskihajonnan päähän keskiarvosta”,

Or,

Or,

Olen varma, että 89 %:n kaikesta datasta pitäisi osua 3 keskihajonnan päähän keskiarvosta”.

Tältä se näyttää mielivaltaisen näköiselle jakaumalle,

Miten sitä sovelletaan?

Kuten voit jo arvata, data-analyysisi perusmekaniikan ei tarvitse muuttua miksikään. Keräät edelleen otoksen datasta (mitä suurempi, sitä parempi), lasket samat kaksi suuretta, joita olet tottunut laskemaan – keskiarvon ja keskihajonnan – ja sovellat sitten 68-95-99,7-säännön sijasta uusia rajoja.

Taulukko näyttää seuraavalta (tässä k tarkoittaa sitä, että montako keskihajontaa on poissa keskiarvosta),

Videodemo sen soveltamisesta on täällä,

Missä on juju? Miksi ihmiset eivät käytä tätä ”yleispätevämpää” sidettä?

Taulukkoa tai matemaattista määritelmää katsomalla on selvää, mikä on juju. Chebyshevin sääntö on paljon heikompi kuin Gaussin sääntö siinä asiassa, että se asettaa rajoja datalle.

Se noudattaa 1/k² kaavaa verrattuna normaalijakauman eksponentiaalisesti laskevaan kaavaukseen.

Voit esimerkiksi rajata mitä tahansa 95 %:n varmuudella, jos haluat sisällyttää datan 4,5 keskihajontaan asti vs. vain 2 standardipoikkeamaa (normaalijakaumalle).

Mutta se voi silti pelastaa tilanteen, kun data ei näytä lainkaan normaalijakauman kaltaiselta.

Onko mitään parempaa?

On olemassa toinenkin raja nimeltä ”Chernoffin raja”/Hoeffdingin epätasa-arvo (Chernoff Bound)/Hoeffdingin epätasa-arvo, joka antaa riippumattomissa satunnaismuuttujien summille eksponentiaalisen jyrkän pyrstöjakauman (1/k²:een verrattuna).

Tätäkin voidaan käyttää Gaussin jakauman sijasta silloin, kun data ei näytä normaalilta, mutta vain silloin, kun meillä on suuri luottamus siihen, että taustalla oleva prosessi koostuu osaprosesseista, jotka ovat täysin riippumattomia toisistaan.

Epäonnekseen monissa yhteiskunnallisissa ja liiketaloudellisissa tapauksissa lopullinen data on tulosta monien osaprosessien erittäin monimutkaisesta vuorovaikutuksesta, joilla voi olla voimakas keskinäinen riippuvuus.

Yhteenveto

Tässä artikkelissa opimme tietyntyyppisestä tilastollisesta sidonnaisuudesta, jota voidaan soveltaa laajimpaan mahdolliseen datan jakaumaan, joka ei ole riippuvainen normaaliusolettamasta. Tämä on kätevää silloin, kun tiedämme hyvin vähän datan todellisesta lähteestä emmekä voi olettaa sen noudattavan Gaussin jakaumaa. Raja noudattaa potenssilakia eikä eksponentiaalista luonnetta (kuten Gaussin jakauma) ja on siksi heikompi. Se on kuitenkin tärkeä työkalu repertuaarissasi minkä tahansa mielivaltaisen datajakauman analysoimiseksi.