Miksi 0.999… on yhtä kuin 1?!

Toinen tapa ajatella yhteenlaskun termejä on, että jokainen peräkkäinen termi saadaan kertomalla edellinen termi yhteisellä suhdeluvulla.

Tämä tarkoittaa, että meillä on geometrinen sarja, joka konvergoituu arvoon a/(1 – r), jossa a on sarjan ensimmäinen arvo ja r on suhdeluku, jolla kerromme saadaksemme seuraavan termin.

Sarjan konvergenssi tarkoittaa yksinkertaisesti sitä, että sarja tulee yhä lähemmäs ja lähemmäs tiettyä arvoa, kun sarjaan lisätään yhä enemmän termejä. Sarja tulee äärettömän lähelle konvergenssiarvoa. Äärettömässä mittakaavassa konvergenssi muuttuu tasa-arvoiseksi.

Tapauksessamme aloitamme arvosta 1/10 ja kerromme joka kerta 1/10:llä, joten sekä a että r = 1/10.

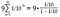
Suorita aritmeettinen laskutoimitus oikealla puolella.

Nyt olemme muodollisesti osoittaneet, että 0.999… konvergoi tai on yhtä kuin 1.

Loppuajatuksia & Inspiraatio

Jos tämä tuntuu sinusta oudolta, se on hyvä! Tiedät, että kahden eri luvun, pitäisi itse asiassa olla eri lukuja. Tämän ongelman intuitionvastainen luonne on luontainen osa sitä outoutta, joka liittyy äärettömyyden kanssa työskentelyyn.

Jopa tämän kaltaisessa yksinkertaisessa ongelmassa siirrytään ihmisaivoille käsin kosketeltavasta rajasta mittakaavaan, joka on tavallaan käsityskykymme ulkopuolella. Finiittisinä olentoina voimme tarttua äärettömyyden tai ikuisuuden käsitteen ymmärtämiseen, mutta emme voi koskaan todella kokea sitä. Mikä tarkoittaa sitä, että usein se, minkä tiedämme olevan totta meidän äärellisessä maailmassamme, osoittautuu käyttäytyvän eri tavalla äärettömällä tasolla.

Se, että hyväksymme siirtymän helposti havaittavasta ja toistettavasta matematiikasta siihen, mitä voimme vain testata ja kuvitella mielessämme, on osa matematiikan kauneutta ja ihmeellisyyttä.

Älkää siis ottako tämänpäiväistä oppituntia nimellisarvoonsa ja kohauttako olkapäitänne pois.

Olkoon sumukerroksenne välissänne täydellisestä ymmärryksestä. Anna mielesi räjähtää siitä, että äärettömyys käyttäytyy oudosti. Ja anna sen saada sinut kaipaamaan lisää ymmärrystä ja ennen kaikkea lisää matematiikkaa.

Kiitos, että luit ja pohdit ääretöntä kanssani tänään!