Funktiot tai kartoitus

Funktioissa tai kartoituksessa opiskelemme nyt erityyppisiä suhteita, joita kutsutaan funktioiksi tai kartoitukseksi. Niiden ymmärtämiseksi otetaan muutama tosielämän esimerkki.

Kaikkiin näihin kysymyksiin on
yksikäsitteiset vastaukset. Katsotaanpa
miten voimme liittää
tämän oppimiskartoitukseen.

● Mistä aurinko nousee?

Idästä

● Mikä on Intian pääkaupunki?

Delhi

● Mikä on 4:n seuraaja?

5

● Mikä on 5:n ja 3:n summa?

8

Kartoitus tai funktio:

Jos A ja B ovat kaksi ei-tyhjää joukkoa, niin relaatiota ’f’ joukosta A joukkoon B sanotaan funktioksi tai kartoitukseksi,
● jos jokaisella joukon A alkioyksilöllä on yksikäsitteinen joukon B alkioyksilö.

● Funktiota ’f’ joukosta A joukkoon B merkitään sanalla f : A → B.

●● Jos f on funktio A:sta B:hen ja x ∈ A, niin f(x) ∈ B, missä f(x):tä kutsutaan x:n kuvaksi f:n alaisuudessa ja x:ää kutsutaan f(x):n esikuvaksi ’f:n’ alaisuudessa.

Huomautus:

Jotta f olisi kuvaaja A:sta B:hen:

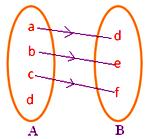
● Jokaisella A:n alkioilla on oltava kuva B:ssä. Viereinen kuva ei esitä kartoitusta, koska joukon A alkio d ei liity mihinkään joukon B alkioon.

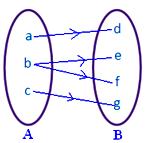
● Yhdelläkään joukon A alkioilla ei saa olla useampaa kuin yhtä kuvaa. Viereinen kuva ei esitä kuvaa, koska joukon A alkio b liittyy kahteen joukon B alkioon d, f.

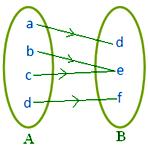
● A:n eri alkioilla voi olla sama kuva joukossa B. Viereinen kuva esittää kartoitusta.

Huomautus:

Jokainen kartoitus on relaatio, mutta jokainen relaatio ei välttämättä ole kartoitus.

Funktio erityisenä relaationa:

Palautetaan mieleen ja käydään läpi funktio erityisenä relaationa Oletetaan, että A ja B ovat kaksi ei-tyhjää joukkoa, niin sääntöä ’f’, joka liittää jokaisen A:n alkion yhteen ainoaan B:n alkioon, sanotaan funktioksi tai A:n ja B:n väliseksi kartoitukseksi.
Jos ’f’ on mappaus A:sta B:hen,

ilmaisemme sen muodossa f: A → B

luemme sen muodossa ’f’ on funktio A:sta B:hen.
Jos ’f ’ on funktio A:sta B:hen ja x∈A ja y∈B, sanomme, että y on alkion x kuva funktiossa ’ f ’ ja merkitsemme sitä f(x).
Kirjoitamme siis y = f(x)

Tässä tapauksessa elementtiä x kutsutaan y:n esikuvaksi.

Jos kyseessä on funktio A:sta B:hen.
● A:n ja B:n tulee olla ei-tyhjiä.

● Jokaisella A:n elementillä pitäisi olla kuva B:ssä.

● Millään A:n elementillä ei pitäisi olla useampaa kuin yhtä kuvaa B:ssä.
Huomautus:

● Kahdella tai useammalla ’A:n’ elementillä voi olla sama kuva B:ssä.

● f : x → y tarkoittaa, että funktiolla ’f’ funktiosta ’A:sta B:hen ’A:n’ elementillä x on kuva y B:ssä.

● Jokaisen f:n kuvan on oltava B:ssä, mutta B:ssä voi olla joitain elementtejä, jotka eivät ole f:n mielikuvia yhdellekään ’A:n’ elementille.

● Relaatiot ja kuvaukset

Orjestetty pari

Kahden joukon kartesiolainen tulo

Relaatio

Relaation alue ja kantama

Funktiot tai kuvaukset

Relaation Co-Funktion domain and Range of Function

● Relaatiot ja kartoitus – Työpaperit

Työpaperi matematiikan relaatioista

Työpaperi funktioista tai kartoituksesta

7. luokan matematiikkaongelmat

8. luokan matematiikan harjoittelu
Funktioista tai kartoituksesta KOTISIVULLE