2.12: Van der Waalsin yhtälö

Van der Waalsin yhtälö laajentaa ideaalikaasun yhtälöä yksinkertaisella tavalla. Van der Waalsin yhtälö on

\

Se sopii todellisen kaasun paine-tilavuus-lämpötilatietoihin paremmin kuin ideaalikaasun yhtälö. Parempi sovitus saadaan ottamalla käyttöön kaksi parametria (nimetty ”\(a\)” ja ”\(b\)”), jotka on määritettävä kokeellisesti kullekin kaasulle. Van der Waalsin yhtälö on erityisen hyödyllinen pyrkiessämme ymmärtämään todellisten kaasujen käyttäytymistä, koska se sisältää yksinkertaisen fysikaalisen kuvan todellisen kaasun ja ideaalikaasun välisestä erosta.

Johdettaessa Boylen lakia Newtonin laeista oletamme, että kaasumolekyylit eivät ole vuorovaikutuksessa keskenään. Yksinkertaiset argumentit osoittavat, että tämä voi pitää paikkansa vain likimain. Todellisten kaasumolekyylien täytyy olla vuorovaikutuksessa toistensa kanssa. Lyhyillä etäisyyksillä ne hylkivät toisiaan. Hieman pidemmillä etäisyyksillä ne vetävät toisiaan puoleensa. Ideaalikaasun yhtälö voidaan johtaa myös 10 §:ssä esitetyistä perusoletuksista soveltamalla tilastollisen termodynamiikan teoriaa. Tekemällä erilaisia oletuksia molekyylien ominaisuuksista voimme soveltaa tilastollista termodynamiikkaa johdettaessa \({}^{5}\) van der Waalsin yhtälöä. Tarvittavat oletukset ovat, että molekyylit vievät äärellisen tilavuuden ja että ne vetävät toisiaan puoleensa voimalla, joka muuttuu niiden välisen etäisyyden käänteisvoimana. (Vetovoiman oletetaan yleensä olevan verrannollinen \(r^{-6}\).)

Tunnistaaksemme, että todelliset kaasumolekyylit sekä vetävät toisiaan puoleensa että hylkivät toisiaan, meidän on vain muistettava, että mikä tahansa kaasu voidaan nesteyttää alentamalla sen lämpötilaa ja lisäämällä siihen kohdistuvaa painetta. Jos jäähdytämme nestettä edelleen, se jäätyy kiinteäksi. Kiinteän aineen kaksi tunnusomaista piirrettä ovat, että se säilyttää muotonsa ja että se on lähes kokoonpuristumaton. Kiinteän aineen kokoonpuristumattomuus johtuu sen muodostavien molekyylien välisistä hylkivistä voimista; ne ovat tulleet niin lähelle toisiaan, että niiden välisistä hylkivistä voimista on tullut tärkeitä. Jotta kiinteä aine saataisiin puristettua kokoon, molekyylit on työnnettävä vielä lähemmäs toisiaan, mikä vaatii kohtuuttomia voimia. Toisaalta, jos heitämme jääkuution huoneen poikki, kaikki siihen kuuluvat vesimolekyylit lentävät huoneen poikki yhdessä. Ilmeisesti kiinteässä aineessa olevat vesimolekyylit vetävät toisiaan puoleensa, sillä muuten ne kaikki lähtisivät omille teilleen – jääkuution heittäminen olisi kuin kourallisen kuivan hiekan heittäminen. Vesimolekyylit ovat kuitenkin samoja molekyylejä lämpötilasta tai paineesta riippumatta, joten jos niiden välillä on kiinteässä olomuodossa veto- ja hylkimisvoimia, näiden voimien on oltava läsnä myös neste- ja kaasufaasissa.

Kaasufaasissa molekyylit ovat kaukana toisistaan; neste- tai kiinteässä olomuodossa ne ovat pakkautuneet yhteen. Kiehumispisteessään nesteen tilavuus on paljon pienempi kuin sen kaasun tilavuus, josta se on tiivistetty. Jäätymispisteessä kiinteän aineen tilavuus eroaa vain vähän sen nesteen tilavuudesta, josta se on jäätynyt, ja se on varmasti suurempi kuin nolla. Nämä arkipäiväiset havainnot selittyvät helposti, jos oletetaan, että millä tahansa molekyylillä on ominaistilavuus. Voimme puolestaan ymmärtää tämän olevan seurausta molekyylien välisten voimien luonteesta; ilmeisesti nämä voimat voimistuvat, kun molekyyliparin välinen etäisyys pienenee. Koska nesteellä tai kiinteällä aineella on tietty tilavuus, repulsiivisen voiman on kasvettava nopeammin kuin vetovoiman, kun molekyylien välinen etäisyys on pieni. Usein on hyödyllistä puhua tiivistetyn faasin molaarisesta tilavuudesta. Moolitilavuudella tarkoitetaan puhtaan aineen yhden moolin tilavuutta. Kondensoituneen faasin molaarinen tilavuus määräytyy sen molekyylien välisen etäisyyden mukaan, jossa molekyylien väliset veto- ja hylkimisvoimat ovat tasapainossa.

Kondensoituneissa faaseissa molekyylit ovat ilmeisesti hyvin lähellä toisiaan. Jos oletetaan, että molekyylien väliset tyhjät tilat ovat merkityksettömiä, tiivistetyn faasin tilavuus on suunnilleen yhtä suuri kuin näytteen molekyylien lukumäärä kerrottuna yhden molekyylin tilavuudella. Tällöin molaarinen tilavuus on Avogadron luku kertaa yhden molekyylin viemä tilavuus. Jos tiedämme tiheyden, D, ja moolimassan, \(\overline{M}\), voimme löytää moolitilavuuden, \(\overline{V}\), seuraavasti

\

Tilavuus, jonka yksi molekyyli vie, V\({}_{molekyyli}\), tulee

\

Van der Waalsin yhtälössä esiintyvät paine ja tilavuus ovat todellisen kaasun paine ja tilavuus. Voimme liittää van der Waalsin yhtälön termit ideaalikaasun yhtälöön: On hyödyllistä ajatella termejä \(\vasen(P+{{an}^2}/{V^2}\oikea)\) ja \(\vasen(V-nb\oikea)\) hypoteettisen ideaalikaasun paineena ja tilavuutena. Eli

\ &=nRT \end{align*}\]

Tällöin meillä on

\

Johdamme ideaalikaasun yhtälön mallista, jossa molekyylit ovat vuorovaikuttamattomia pistemassoja. Ideaalikaasun tilavuus on siis tilavuus, jonka vie kaasu, jonka yksittäisillä molekyyleillä on nollatilavuus. Jos todellisen kaasun yksittäiset molekyylit vievät tehokkaasti tilavuuden \({b}/{\overline{N}}}\), niin \(n\) moolia niistä vie tehokkaasti tilavuuden

\

Van der Waalsin yhtälö sanoo, että todellisen kaasun tilavuus on tilavuus, jonka ei-vuorovaikutteiset pistemäiset massat miehittäisivät, \(V_{³”ideaalinen\”-kaasun{³”\)\)\), lisättynä itse kaasumolekyylien tehokkaalla tilavuudella. (Kun todellisia kaasumolekyylejä koskevat tiedot sovitetaan van der Waalsin yhtälöön, \(b\):n arvo on yleensä jonkin verran suurempi kuin nesteen tiheyden ja molekyylipainon perusteella arvioitu tilavuus. Ks. ongelma 24.)

Samoin meillä on

\

Voidaan ymmärtää tämä loogisena seurauksena todellisen kaasun molekyylien välisistä vetovoimaisista vuorovaikutuksista. Kun \(a>0\), se sanoo, että todellisen kaasun paine on pienempi kuin hypoteettisen ideaalikaasun paine määrällä, joka on verrannollinen \({\left({n}/{V}\right)}^2\). Suhteellisuusvakio on \(a\). Koska \({n}/{V}\) on kaasumolekyylien molaarinen tiheys (mooleja tilavuusyksikköä kohti), se on pitoisuuden mitta. Samanlaisten molekyylien välisten törmäysten määrä on verrannollinen niiden konsentraation neliöön. (Tarkastelemme tätä seikkaa yksityiskohtaisemmin luvuissa 4 ja 5.) Joten \({\left({n}/{V}\right)}^2\) on sen taajuuden mitta, jolla todelliset kaasumolekyylit joutuvat läheiseen kosketukseen toistensa kanssa. Jos ne vetävät toisiaan puoleensa tullessaan lähelle toisiaan, tämän vetovoiman vaikutuksen pitäisi olla verrannollinen \({\\left({n}/{V}\right)}^2\). Van der Waalsin yhtälö on siis sopusoinnussa sen ajatuksen kanssa, että todellisen kaasun paine eroaa hypoteettisen ideaalikaasun paineesta määrällä, joka on verrannollinen vetovoimaisten vuorovaikutusten esiintymistiheyteen ja voimakkuuteen.

Mutta miksi vetovoimaisilla vuorovaikutuksilla pitäisi olla tämä vaikutus; miksi todellisen kaasun paineen pitäisi olla pienempi kuin hypoteettisen ideaalikaasun paineen? Ehkä paras tapa kehittää laadullinen kuva on tunnustaa, että vetovoimaisilla molekyylien välisillä voimilla on taipumus saada kaasumolekyylit kasaantumaan. Loppujen lopuksi juuri nämä vetovoimatovat ne, jotka saavat molekyylit pakkautumaan nesteeksi alhaisissa lämpötiloissa. Kiehumispisteen yläpuolella kaasumolekyylien kyky kulkea omia teitään rajoittaa tämän taipumuksen vaikutuksia; kuitenkin myös kaasussa vetovoimien on toimittava tavalla, joka pyrkii pienentämään molekyylien viemiä tilavuuksia. Koska kaasun viemä tilavuus määräytyy säiliön koon – ei itse kaasun ominaisuuksien – mukaan, tämä kasautumistaipumus ilmenee paineen laskuna.

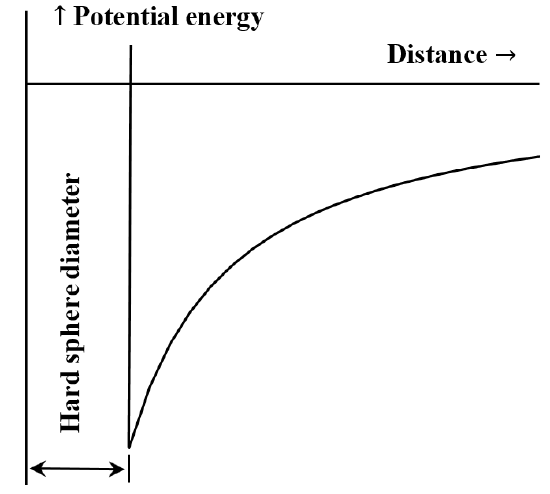
Hiukkasten tai kemiallisten osien välistä vuorovaikutusta on usein hyödyllistä kuvata potentiaalienergian ja etäisyyden välisen diagrammin avulla. Van der Waalsin yhtälö vastaa tapausta, jossa molekyylien välinen repulsiivinen vuorovaikutus on olematon, kunnes molekyylit joutuvat kosketuksiin. Kun ne ovat joutuneet kosketuksiin, energia, joka tarvitaan niiden siirtämiseksi vielä lähemmäs toisiaan, kasvaa mielivaltaisen suureksi. Usein tätä kuvataan sanomalla, että ne käyttäytyvät kuin ”kovat pallot”. Kahden molekyylin välinen vetovoima pienenee, kun niiden välinen etäisyys kasvaa. Kun ne ovat hyvin kaukana toisistaan, vetovoima on hyvin pieni. Sanomme, että vuorovaikutuksen energia on nolla, kun molekyylit ovat äärettömän kaukana toisistaan. Jos meillä on aluksi kaksi kaukana toisistaan olevaa, paikallaan olevaa, toisiaan puoleensa vetävää molekyyliä, ne liikkuvat spontaanisti toisiaan kohti ja saavat samalla liike-energiaa. Niiden potentiaalienergia pienenee niiden lähestyessä toisiaan ja saavuttaa pienimmän arvonsa, kun molekyylit kohtaavat toisensa. Näin ollen van der Waalsin yhtälöstä seuraa kuvassa 5 hahmoteltu potentiaalienergian ja etäisyyden välinen diagrammi.