Suma del producto (SOP) y producto de la suma (POS)
On noviembre 10, 2021 by adminProducto de la suma (POS) & Suma del producto (SOP)
Tabla de contenidos
Suma del producto (SOP)
Suma del producto es la forma abreviada de SOP. La forma de suma del producto es una forma de expresión en el álgebra booleana en la que se suman diferentes términos de producto de las entradas. Este producto no es una multiplicación aritmética sino que es un AND lógico booleano y la suma es un OR lógico booleano.
Para entender mejor el SOP, necesitamos conocer el término mínimo.
Término mínimo
El término mínimo significa el término que es verdadero para un número mínimo de combinaciones de entradas. Eso es cierto para una sola combinación de entradas.
Dado que la puerta AND también da Verdadero sólo cuando todas sus entradas son verdaderas por lo que podemos decir que los términos min son AND de combinaciones de entrada como en la tabla dada a continuación.
3 entradas tienen 8 combinaciones diferentes. Cada combinación tiene un término mínimo denotado por una pequeña m y su número de combinación decimal escrito en el subíndice. Cada uno de estos mintérminos sólo será verdadero para la combinación de entrada específica.
- También puedes leer: Contador digital asíncrono (contador de ondulación) – Tipos, funcionamiento & Aplicación
Tipos de formas de suma de producto (SOP)
Hay pocas formas diferentes de suma de producto.
- Forma SOP canónica
- Forma SOP no canónica
- Forma SOP mínima
Forma SOP canónica
Esta es la forma estándar de Suma de Producto. Está formada por O Ring los minterms de la función para la que la salida es verdadera. También se conoce como suma de términos mínimos o forma normal disyuntiva canónica (CDNF). Es sólo un nombre elegante. «canónica» significa «normalizada» y «disyuntiva» significa «unión lógica O».
La expresión SOP canónica está representada por el signo de suma ∑ y los términos mínimos en las llaves para los que la salida es verdadera.
Por ejemplo, a continuación se da una tabla de verdad de una función.

Para esta función la expresión SOP canónica es
F = ∑( m1, m2, m3, m5 )
Lo que significa que la función es verdadera para los términos mínimos {1, 2, 3, 5}.
Expandiendo el sumatorio obtenemos.
F = m1 + m2 + m3 + m5
Ahora poniendo los términos min en la expresión
F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
La forma canónica contiene todas las entradas complementadas o no complementadas en sus términos producto.
También puedes leer: Contador digital síncrono – Tipos, funcionamiento &Aplicaciones
Forma SOP no canónica
Como su nombre indica, esta forma es la forma no estandarizada de las expresiones SOP. Los términos del producto no son los términos mínimos pero están simplificados. Tomemos como ejemplo la función anterior en forma canónica.
F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
F = A̅B̅C + A̅B(C̅ + C) + AB̅C
F = A̅B̅C + A̅B(1) + AB̅C
F = A̅B̅C + A̅B + AB̅C
Esta expresión sigue estando en forma de Suma de Productos pero no escanónica o forma no estandarizada.
Forma SOP mínima
Esta forma es la expresión SOP más simplificada de una función. También es una forma no canónica. La forma SOP mínima puede hacerse utilizando teoremas algebraicos booleanos, pero es muy fácil hacerla utilizando el mapa de Karnaugh (K-map).
Se prefiere la forma SOP mínima porque utiliza el mínimo número de compuertas y líneas de entrada. es comercialmente beneficiosa por su tamaño compacto, velocidad rápida y bajo coste de fabricación.
Tomemos un ejemplo de la función dada anteriormente en forma canónica.

Su mapa K se da a continuación.
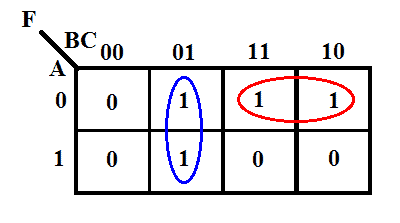
De acuerdo con el K-map, la expresión de salida será
F = B̅C + A̅B
Esta es la expresión más simplificada &optimizada para dicha función. Esta expresión requiere sólo dos puertas AND de 2 entradas & una puerta OR de 2 entradas. Sin embargo, la forma canónica necesita cuatro compuertas AND de 3 entradas & una compuerta OR de 4 entradas, lo cual es relativamente más costoso que la implementación de la forma mínima.
- También puedes leer: Contador de anillo & Contador de Johnson – Construcción & Funcionamiento
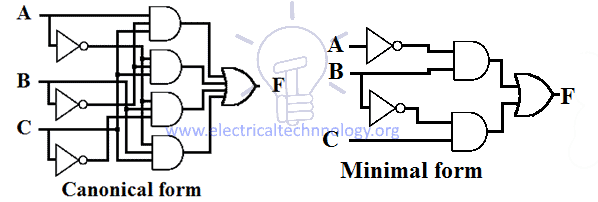
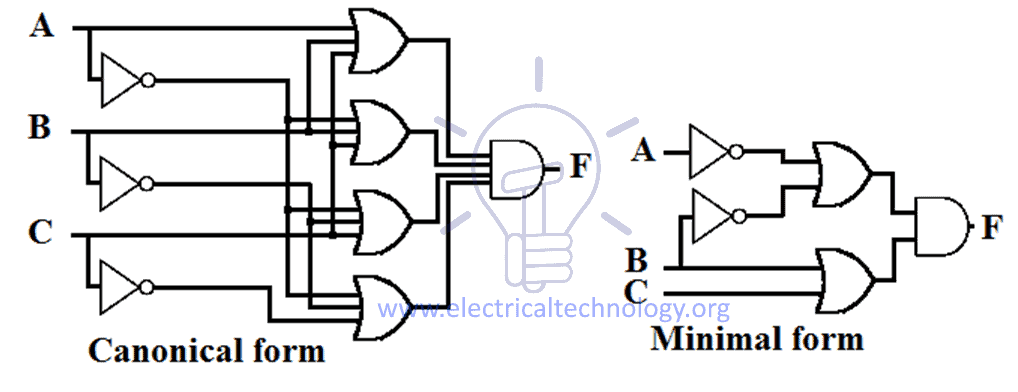
Diseño esquemático de la suma del producto (SOP)
La expresión SOP implementa un diseño AND-OR de 2 niveles en el que la puerta de primer nivel es una puerta AND que sigue a la puerta de segundo nivel que es una puerta OR. El diseño esquemático de la expresión SOP necesita un grupo de compuertas AND & y una compuerta OR.
Todas las expresiones SOP tienen el mismo diseño, es decir, todas las entradas pasan por la compuerta AND y luego la salida de estas compuertas AND fluye a través de una compuerta OR como se muestra en la figura siguiente.
El número de entradas y el número de compuertas AND dependen de la expresión que se esté implementando.
Un ejemplo de diseños de expresión SOP canónica y mínima para una función se da a continuación.
Conversión de la forma SOP mínima a la canónica
La conversión de la forma mínima o de cualquier tipo de forma no canónica a la forma canónica es muy simple.
Como sabemos la forma canónica tiene términos mínimos & Los términos mínimos consisten en todas las entradas ya sean complementadas o no complementadas. Así que vamos a multiplicar cada término de SOP mínimo con la suma de la forma complementada y no complementada de la entrada que falta. A continuación se da un ejemplo de conversión para la función anterior en forma SOP mínima.
Forma SOP mínima
F = A̅B + B̅C
Al término A̅B le falta la entrada C. Así que multiplicaremos A̅B con (C+C̅) porque (C+C̅ = 1). Al término B̅C le falta la entrada A. por lo que se multiplicará por (A+A̅)
F = A̅B(C + C̅) + B̅C(A + A̅)
F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C
Ahora, esta expresión está en forma canónica.
Conversión de SOP canónico a POS canónico
La expresión SOP estándar puede convertirse en expresión POS estándar (producto de la suma). Por ejemplo, la función dada anteriormente está en forma SOP canónica
F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
F = ∑ ( m1, m2, m3, m5 )
Los términos restantes de esta función son maxterms para los que la salida es falsa. Estos términos max son M0,M4,M6,M7. Estos términos max se utilizarán en la expresión POS como el producto de estos términos max. El símbolo del producto es ∏.
F = ∏ ( M0, M4, M6, M7)
F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C)(A̅+B̅+C̅)
Los términos Max son el complemento de los minterms. Por lo que M0=(A+B+C).
- También puedes leer: Ripple Carry And Carry Look Ahead Adder
Conversión de SOP canónico a SOP mínimo
El SOP canónico puede ser convertido a SOP mínimo. Se puede convertir utilizando el mapa de Karnaugh o los teoremas algebraicos de Boole. El método del mapa K es muy fácil y su ejemplo se ha hecho arriba en la forma SOP mínima.
Producto de la suma
Producto de la suma abreviado para POS.
La forma del producto de la suma es una forma en la que se toman productos de diferentes términos de suma de entradas. No son producto y suma aritméticos, sino que son lógicos booleanos AND y OR respectivamente.
Para entender mejor el producto de la suma, necesitamos conocer el término Max.
Término Max
Maxterm significa el término o expresión que es verdadero para un número máximo de combinaciones de entrada o que es falso para una sola combinación de entradas.
Como la puerta OR también da falso para una sola combinación de entrada. Así que Maxterm es OR de entradas complementadas o no complementadas.
Los términos máximos para 3 variables de entrada se dan a continuación.
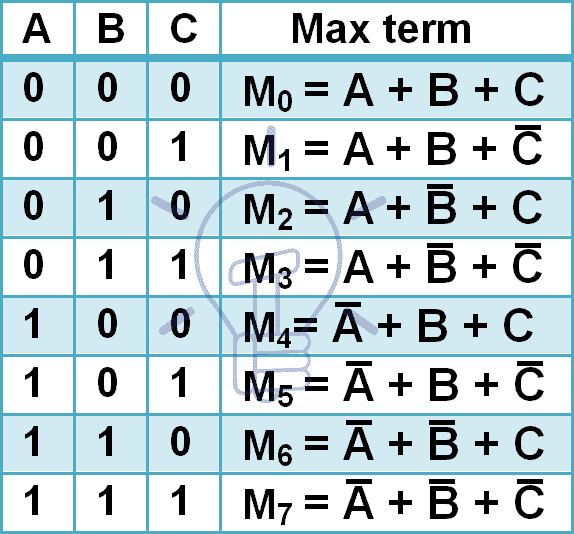
3 entradas tienen 8 combinaciones diferentes por lo que tendrá 8 maxterms. Los maxterms se denotan con M mayúscula y el número de combinación decimal en el subíndice como se muestra en la tabla dada anteriormente.
En el maxterm, cada entrada se complementa porque el Maxterm da ‘0’ sólo cuando se aplica la combinación mencionada y el Maxterm es complemento del minterm.
M3 = m̅3
M3 = (A̅BC)’
M3 = A + B̅ +C̅ DE la ley de Morgan
Por lo que para A=0 el Maxterm consiste en A & para A=1 el Maxterm consiste en A̅.
También puede leer: Flip-Flops digitales – Flip Flops SR, D, JK y T
Tipos de producto de formas de suma
Hay diferentes tipos de producto de formas de suma.
- Forma POS canónica
- Forma no canónica
- Forma POS mínima
Forma POS canónica
También se conoce como Producto de término máximo o forma normal conjuntiva canónica (CCNF). Canónico significa norma y conjuntivo significa intersección.
En esta forma, los Maxterms son Y juntos para los que la salida es falsa.
La expresión POS canónica se representa por ∏ y los Maxterms para los que la salida es falsa entre paréntesis como se muestra en el ejemplo dado a continuación.

F = ∏ (M0, M4, M6, M7)
Ampliando el producto
F = M0.M4.M6.M7
Poniendo términos Max
F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)
La forma canónica contiene todas las entradas complementadas o no complementadas en su cada término de la suma.
- También puedes leer: Clap Switch Circuit Electronic Project Using 555 Timer
Forma no canónica
El producto de la expresión de la suma que no está en forma estándar se llama forma no canónica.
Tomemos la función dada anteriormente como un ejemplo.
F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)
F = (B+C) (A̅+B̅+C)(A̅+B̅+C̅)
Los mismos términos pero invertidos eliminan de dos términos Max y forman un solo término para demostrarlo aquí hay un ejemplo.
= (A+B+C) (A̅+B+C)
= AA̅+AB+AC+A̅B+BB+BC+A̅C+BC+CC
= 0+AB+AC+A̅B+A̅C+B+BC+C
= A(B+C)+A̅(B+C)+B(1+C)+C
= (B+C)(A+A̅)+B(1)+C
= (B+C)(0)+B+C
= B+C
La expresión conseguida sigue estando en forma de Producto de la Suma, pero no esforma canónica.
Forma POS mínima
Esta es la forma más simplificada y optimizada de una expresión POS que no es canónica. La forma mínima del producto de la suma puede lograrse utilizando teoremas algebraicos booleanos como en el ejemplo no canónico dado anteriormente. Otro método para lograr la forma POS mínima es mediante el uso del mapa de Karnaugh que es comparativamente más fácil que el uso de los teoremas algebraicos booleanos.
La forma POS mínima utiliza menos número de entradas y puertas lógicas durante su implementación, es por eso que están siendo preferidos sobre la forma canónica por su implementación compacta, rápida y de bajo costo.
Tomemos como ejemplo la función dada anteriormente
Mapa K de la función
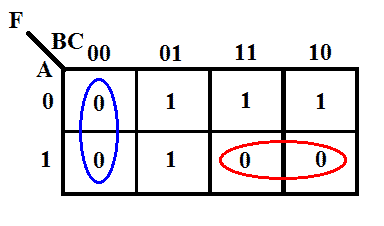
Expresión mínima utilizando el mapa K
F = (B+C) (A̅+B̅)
La expresión conseguida es el producto mínimo de la forma de suma. Sigue siendo la expresión del producto de la suma, pero sólo necesita 2 entradas, dos compuertas OR y una única compuerta AND de 2 entradas. Sin embargo, la forma canónica necesita 4 compuertas OR de 3 entradas y 1 compuerta AND de 4 entradas.
- También puedes leer: Sistemas de retroalimentación negativa y amplificadores de retroalimentación negativa
Diseño esquemático del producto de la suma (POS)
La expresión del producto de la suma tiene un diseño esquemático específico de OR-AND. En OR-AND las entradas pasan por una matriz de compuertas OR que es el primer nivel de compuertas, la salida de las compuertas OR de primer nivel pasa por el segundo nivel de la compuerta, que es una compuerta AND.
El número de entradas y el número de compuertas utilizado en este diseño depende de la expresión que se va a implementar.
La forma canónica consiste en el máximo número de entradas y compuertas posibles, sin embargo, la forma mínima consiste en el menor número posible de entradas y compuertas. El diseño esquemático de la forma canónica y mínima de POS se da a continuación.
Conversión de POS mínimo a forma canónica POS
Como sabemos la forma canónica de POS tiene términos máximos y los términos máximos contienen cada entrada ya sea complementada o no complementada. Así que vamos a añadir cada término de la suma con el producto de la entrada complementada y no complementada que falta. Ejemplo de su conversión se da a continuación.
Forma POS mínima
F = (A̅+B̅) (B+C)
(A̅+B̅) término falta la entrada C así que añadiremos (CC̅) con ella. Al término (B+C) le falta la entrada A por lo que añadiremos (AA̅) con él.
F = (A̅+B̅+CC̅) (B+C+AA̅)
F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)(A̅+B+C)
Esta expresión está ahora en forma canónica.
- También puede leer: Contador y tipos de contadores electrónicos
Conversión de POS canónico a SOP
El producto de la expresión Suma puede convertirse en forma Suma de Producto sólo si la expresión está en forma canónica. El POS canónico y el SOP canónico son interconvertibles, es decir, se pueden convertir el uno en el otro. A continuación se presenta un ejemplo de conversión de POS a SOP.
POS forma canónica
F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)
En la forma canónica cada término de la suma es un término máximo por lo que también se puede escribir como:
F = ∏(M0,M4,M6,M7)
Las restantes combinaciones de entradas son minterms de la función para los que su salida es verdadera. Para convertirla en expresión SOP primero cambiaremos el símbolo a sumatorio (∑) y utilizaremos el minterm restante.
F = ∑ (m1,m2,m3,m5)
Ahora expandiremos el signo de sumatorio para formar la expresión SOP canónica.
F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
Los términos mínimos son el complemento de los términos máximos para la misma combinación de entradas.
POS canónico a mínimo
Una expresión canónica de producto de suma puede convertirse en producto mínimo de forma de suma utilizando el mapa de Karnaugh (K-map). Otro método para convertir la canónica en mínima es mediante el uso de teoremas algebraicos booleanos.
El uso del mapa K es muy fácil por eso se prefiere el mapa K. Para la expresión POS mínima, los 0 en K-map se combinan en grupos y la expresión que obtenemos es complementada ya que los grupos fueron hechos de ‘0’. Su ejemplo se ha hecho arriba.
También puede leer:
- Puerta NOT de lógica digital – Puerta NAND de lógica digital
- Puerta NOR exclusiva (XNOR) de lógica digital
- Puerta NOR de lógica digital
- Puerta NAND de lógica digital
Deja una respuesta