» Qué tamaño tiene una célula de E. coli y cuál es su masa?

¿Cuál es el tamaño de una célula de E. coli y cuál es su masa?

Modo lector

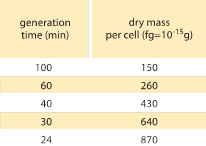
Tabla 1: Relación entre la masa bacteriana y el tiempo de división. La masa seca por célula se da en función del tiempo de generación (duplicación). Se sugiere que la masa aumenta aproximadamente de forma exponencial con la tasa de crecimiento, tal y como observaron originalmente M. Schaechter et al J. Gen. Microbiol., 19:592, 1958. El peso seco de las células se calculó utilizando un valor de 173 µg por unidad de OD460 de un mL (BNID 106437). La cepa utilizada es B/r, una cepa comúnmente utilizada en los primeros estudios de fisiología bacteriana. Valores tomados de F. C. Neidhardt, «Escherichia coli and Salmonella: Cellular and Molecular Biology», Vol. 1., Capítulo 3, ASM Press, 1996.

El tamaño de una bacteria típica como E. coli sirve como regla estándar conveniente para caracterizar las escalas de longitud en biología molecular y celular. Una «regla general» basada en generaciones de mediciones de microscopía óptica y electrónica para las dimensiones de una célula de E. coli es asignarle un diámetro de aproximadamente ≈1µm, una longitud de ≈2µm y un volumen de ≈1µm3 (1 fL) (BNID 101788). La forma puede aproximarse a la de un esferocilindro, es decir, un cilindro con casquetes semiesféricos. Teniendo en cuenta el diámetro y la longitud citados, podemos calcular una estimación más precisa del volumen de ≈1,3 µm3 (5π/12 para ser exactos). La diferencia entre este valor y el valor de la regla empírica citado anteriormente muestra el nivel de inconsistencia con el que vivimos cómodamente cuando utilizamos reglas empíricas. Una de las vías más sencillas para estimar la masa de una bacteria es aprovechar el volumen de ≈1 µm3 de una célula de E. coli y suponer que tiene la misma densidad que el agua. Esta estimación ingenua da lugar a otro valor estándar, a saber, que una bacteria como E. coli tiene una masa de ≈1 pg (pico=10-12). Dado que la mayoría de las células son aproximadamente 2/3 de agua (BNID 100044, 105482) y que los demás componentes, como las proteínas, tienen una densidad característica de aproximadamente 1,3 veces la densidad del agua (BNID 101502, 104272), la conversión de volumen celular a masa es precisa en aproximadamente un 10%.

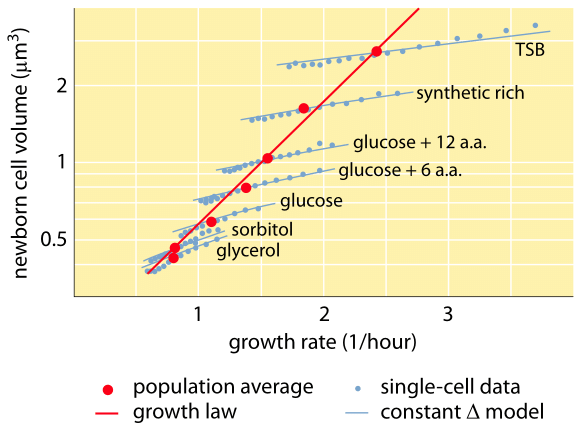
Fig. 1: Relación entre el volumen celular y la tasa de crecimiento. Mediante el uso de microscopía y dispositivos microfluídicos se puede medir el volumen celular a nivel de una sola célula en diversas condiciones, confirmando que el volumen celular medio crece exponencialmente con la tasa de crecimiento. Por el contrario, la variación entre las células para una condición determinada tiene una escala diferente. La variación en el comportamiento de una sola célula se utiliza para probar modelos de regulación del tamaño celular. (Adaptado de S. Taheri-Araghi et al., Curr. Biol. 25:385, 2015.)

Uno de los resultados clásicos de la fisiología bacteriana destaca que la plasticidad en las propiedades de las células se deriva de la dependencia de la masa celular de la tasa de crecimiento. Dicho de forma sencilla, las tasas de crecimiento más rápidas están asociadas a células más grandes. Esta observación se refiere a los cambios fisiológicos en los que los medios que aumentan la tasa de crecimiento también producen células más grandes, como se muestra en la figura 1. Esto también es cierto desde el punto de vista genético, ya que los estudios de evolución experimental a largo plazo que conducen a tasas de crecimiento más rápidas muestran volúmenes celulares más grandes (BNID 110462). Estas observaciones nos ayudan a disipar el mito de «la célula», en el que la gente, a menudo sin querer, utiliza mediciones sobre una célula para hacer inferencias sobre otros tipos de células o el mismo tipo de célula en condiciones diferentes. Los estudios clásicos de Dennis y Bremer sistematizaron estas mediciones y descubrieron que la masa seca varía, como se muestra en la Tabla 1, desde un valor medio de 148 fg para las células que se dividen cada 100 minutos hasta 865 fg para las que tienen un tiempo de división de 24 minutos, lo que indica una diferencia de más de 5 veces según la tasa de crecimiento. Se ha observado una tendencia similar en otros organismos (por ejemplo, para la levadura en ciernes, BNID 105103). Con un 70% de agua, estos valores corresponden a un rango entre 0,4 y 2,5 µm3 en términos de volumen. ¿Cómo podemos racionalizar los tamaños más grandes para las células que crecen a mayor velocidad? Esta cuestión es objeto de debate hasta la fecha (Molenaar D. et al. MSB 5:323, 2009; Amir, A., Phys. Rev, Let., 112:208102, 2014). Las explicaciones varían desde sugerir que tiene una ventaja en la forma en que se realiza la asignación de recursos hasta afirmar que en realidad es sólo un efecto secundario de tener un período incorporado de unos 60 minutos desde el momento en que una célula decide que ha acumulado suficiente masa para comenzar los preparativos para la división y hasta que termina la replicación del ADN y el acto de la división. Este período de «retardo» aproximadamente constante conduce a una dependencia exponencial de la masa celular media en la tasa de crecimiento en esta línea de razonamiento (Amir, A., Phys. Rev, Let, 112:208102, 2014).

Los métodos para medir el volumen celular van desde el uso de un contador Coulter ((BNID 100004), que infiere el volumen basándose en los cambios en la resistencia de un pequeño orificio a medida que una célula pasa por él, hasta mediciones más directas mediante microscopía de fluorescencia que miden la longitud y el diámetro de las células en diferentes condiciones (Figura 1 y BNID 106577, 111480). Sorprendentemente, el hecho de que los distintos laboratorios no converjan siempre en los mismos valores puede deberse a diferencias en los métodos de calibración o en las cepas y condiciones de crecimiento exactas. Una capacidad sin precedentes para medir la masa celular se consigue pesando eficazmente las células en un voladizo microscópico. Como se ilustra en la Figura 2A, se utiliza el flujo de fluido para forzar una célula hacia adelante y hacia atrás en el voladizo hueco. La medición aprovecha el hecho de que la masa celular afecta a la frecuencia de oscilación del voladizo. Esta frecuencia puede medirse con una precisión fenomenal y utilizarse para inferir masas con una precisión de femtogramos. Al cambiar la dirección del flujo de líquido, la célula queda atrapada durante minutos o más y su tasa de acumulación de masa se mide continuamente a nivel de una sola célula. En la aplicación inicial de esta técnica se demostró que las células individuales que son más grandes también acumulan masa más rápidamente, lo que arroja luz sobre una cuestión que se plantea desde hace tiempo: ¿es el crecimiento celular lineal con el tiempo o se describe más adecuadamente mediante una tendencia aproximadamente exponencial? Las diferencias pueden ser mínimas, pero con estas revolucionarias capacidades se vio claramente que este último escenario representa mejor la situación en varios tipos de células probadas, como se muestra en la figura 2B.

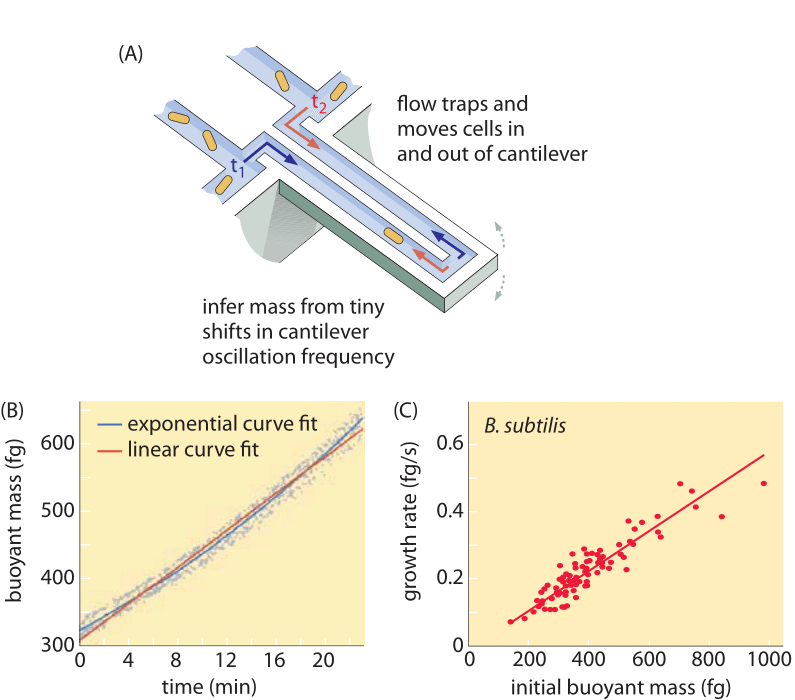
Fig. 2: Utilización de la masa flotante para medir el crecimiento de las células individuales. (A) Un voladizo a escala micrométrica oscila a alta frecuencia y la masa de las células puede determinarse a partir de los cambios en la frecuencia de oscilación. (B) Si se mide a lo largo del tiempo, se obtiene una curva de acumulación de masa de células individuales, como se muestra. (C) Aquí se muestran células de B. subtilis. Se muestra una comparación entre las predicciones de los modelos de crecimiento lineal y exponencial como mejores ajustes. La similitud demuestra lo cerca que están los dos modelos en un rango de sólo dos veces de aumento en el curso del ciclo celular. El peso seco de la célula es aproximadamente 4 veces la masa flotante. (Adaptado de M. Godin et al., Nature Meth. 7:387, 2010.)