¿Qué pasa si sus datos NO son normales?

Introducción

Esta es la semana de Halloween, y entre truco y trato, nosotros, los frikis de los datos, nos reímos con este simpático meme en las redes sociales.

¿Crees que es una broma? Déjenme decirles que esto no es un asunto de risa. Si no podemos asumir que la mayoría de nuestros datos (de origen empresarial, social, económico o científico) son, al menos, aproximadamente «normales» (es decir, generados por un proceso gaussiano o por una suma de múltiples procesos de este tipo), ¡estamos condenados!

Aquí va una brevísima lista de cosas que no serán válidas,

• Todo el concepto de six-sigma
• La famosa regla del 68-95-99,7
• El ‘sagrado’ concepto de p=0,05 (viene del intervalo de 2 sigmas) en el análisis estadístico

¿Asusta lo suficiente? Hablemos más de ello…

La omnipotente y omnipresente distribución normal

Hagamos esta sección corta y dulce.

La distribución normal (gaussiana) es la distribución de probabilidad más conocida. Aquí hay algunos enlaces a los artículos que describen su poder y amplia aplicabilidad,

• ¿Por qué los científicos de datos aman la gaussiana

• Cómo dominar la parte de estadística de su entrevista de ciencia de datos
• ¿Qué es tan importante sobre la distribución normal?

Debido a su aparición en varios dominios y al Teorema Central del Límite (CLT), esta distribución ocupa un lugar central en la ciencia de los datos y la analítica.

Entonces, ¿cuál es el problema?

Todo esto está muy bien, ¿cuál es el problema?

El problema es que a menudo puede encontrar una distribución para su conjunto de datos específicos, que puede no satisfacer la normalidad, es decir, las propiedades de una distribución normal. Sin embargo, debido a la excesiva dependencia de la suposición de normalidad, la mayoría de los marcos de análisis empresarial están hechos a medida para trabajar con conjuntos de datos con distribución normal.

Está casi arraigado en nuestra mente subconsciente.

Digamos que se le pide que detecte si un nuevo lote de datos de algún proceso (ingeniería o negocio) tiene sentido. Por «tener sentido», te refieres a si los nuevos datos pertenecen, es decir, si están dentro del «rango esperado».

¿Qué es esta «expectativa»? ¿Cómo cuantificar el rango?

Automáticamente, como si estuviera dirigido por un impulso subconsciente, medimos la media y la desviación estándar del conjunto de datos de la muestra y procedemos a comprobar si los nuevos datos se encuentran dentro de un determinado rango de desviaciones estándar.

Si tenemos que trabajar con un límite de confianza del 95%, entonces nos alegramos de que los datos se encuentren dentro de 2 desviaciones estándar. Si necesitamos un límite más estricto, comprobamos 3 o 4 desviaciones estándar. Calculamos el Cpk, o seguimos las directrices six-sigma para el nivel de calidad ppm (partes por millón).

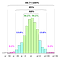
Todos estos cálculos se basan en la suposición implícita de que los datos de la población (NO la muestra) siguen la distribución gaussiana, es decir, el proceso fundamental, a partir del cual los datos de la población se distribuyen.es decir, que el proceso fundamental, a partir del cual se han generado todos los datos (en el pasado y en el presente), se rige por el patrón del lado izquierdo.

¿Pero qué ocurre si los datos siguen el patrón del lado derecho?

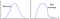
O, esto, y… aquello?

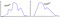
¿Hay un límite más universal cuando los datos NO son normales?

A fin de cuentas, seguiremos necesitando una técnica matemáticamente sólida para cuantificar nuestro límite de confianza, aunque los datos no sean normales. Es decir, nuestro cálculo puede cambiar un poco, pero deberíamos poder decir algo como esto-

«La probabilidad de observar un nuevo punto de datos a cierta distancia de la media es tal y tal…»

Obviamente, tenemos que buscar un límite más universal que los apreciados límites gaussianos de 68-95-99.7 (correspondientes a una distancia de 1/2/3 desviaciones estándar de la media).

Afortunadamente, existe un límite de este tipo llamado «límite de Chebyshev».

¿Qué es el límite de Chebyshev y qué utilidad tiene?

La desigualdad de Chebyshev (también llamada desigualdad de Bienaymé-Chebyshev) garantiza que, para una amplia clase de distribuciones de probabilidad, no más de una determinada fracción de valores puede estar a más de una determinada distancia de la media.

Específicamente, no más de 1/k² de los valores de la distribución pueden estar a más de k desviaciones estándar de la media (o equivalentemente, al menos 1-1/k² de los valores de la distribución están dentro de k desviaciones estándar de la media).

Se aplica a prácticamente todos los tipos de distribuciones de probabilidad y funciona con un supuesto mucho más relajado que el de la normalidad.

¿Cómo funciona?

Incluso si no sabe nada sobre el proceso secreto que hay detrás de sus datos, es muy probable que pueda decir lo siguiente,

«Estoy seguro de que el 75% de todos los datos deberían caer dentro de 2 desviaciones estándar de la media»,

O,

Estoy seguro de que el 89% de todos los datos deberían caer dentro de 3 desviaciones estándar de la media».

Aquí se ve para una distribución de aspecto arbitrario,

¿Cómo aplicarlo?

Como puede adivinar a estas alturas, la mecánica básica de su análisis de datos no necesita cambiar un poco. Seguirá reuniendo una muestra de los datos (cuanto más grande, mejor), calculará las mismas dos cantidades que está acostumbrado a calcular: la media y la desviación estándar, y luego aplicará los nuevos límites en lugar de la regla 68-95-99,7.

La tabla tiene el siguiente aspecto (aquí k denota el número de desviaciones estándar de la media),

Un vídeo demostrativo de su aplicación está aquí,

¿Cuál es el truco? ¿Por qué la gente no utiliza este límite ‘más universal’?

Es obvio cuál es el truco mirando la tabla o la definición matemática. La regla de Chebyshev es mucho más débil que la regla de Gauss en lo que se refiere a poner límites a los datos.

Sigue un patrón de 1/k² en comparación con un patrón de caída exponencial para la distribución Normal.

Por ejemplo, para acotar cualquier cosa con un 95% de confianza, es necesario incluir datos de hasta 4,5 desviaciones estándar frente a

Pero aún puede salvar el día cuando los datos no se parecen en nada a una distribución Normal.

¿Hay algo mejor?

Hay otro límite llamado, «Límite de Chernoff»/desigualdad de Hoeffding que da una distribución de cola exponencialmente aguda (en comparación con el 1/k²) para sumas de variables aleatorias independientes.

También se puede utilizar en lugar de la distribución gaussiana cuando los datos no parecen normales, pero sólo cuando tenemos un alto grado de confianza en que el proceso subyacente se compone de subprocesos que son completamente independientes entre sí.

Desgraciadamente, en muchos casos sociales y empresariales, los datos finales son el resultado de una interacción extremadamente complicada de muchos subprocesos que pueden tener una fuerte interdependencia.

Resumen

En este artículo, aprendimos sobre un tipo particular de límite estadístico que puede aplicarse a la distribución más amplia posible de los datos independientemente del supuesto de Normalidad. Esto resulta útil cuando sabemos muy poco sobre el verdadero origen de los datos y no podemos asumir que siguen una distribución gaussiana. El límite sigue una ley de potencia en lugar de una naturaleza exponencial (como la gaussiana) y, por tanto, es más débil. Pero es una herramienta importante a tener en su repertorio para analizar cualquier tipo de distribución de datos arbitraria.