¿Por qué 0,999… es igual a 1?

Otra forma de pensar en los términos de nuestra suma es que cada término sucesivo se obtiene multiplicando el término anterior por un cociente común.

Eso significa que tenemos una serie geométrica que converge a a/(1 – r) donde a es el primer valor de la serie y r es el cociente por el que multiplicamos para obtener el siguiente término.

La convergencia en una serie simplemente significa que la serie continuará acercándose cada vez más a un valor específico a medida que se añaden más y más términos a la serie. La serie se acerca infinitesimalmente al valor de convergencia. En una escala infinita, la convergencia se convierte en igualdad.

En nuestro caso, empezamos con 1/10 y multiplicamos por 1/10 cada vez, por lo que tanto a como r = 1/10.

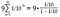
Completa la aritmética del lado derecho.

Ahora hemos demostrado formalmente que 0.999… converge a o es igual a 1.

Pensamientos finales &Inspiración

Si esto te parece extraño, ¡está bien! Usted sabe que dos números diferentes, de hecho, deben ser números diferentes. La naturaleza contraintuitiva de este problema es inherente a la extrañeza que acompaña al trabajo con el infinito.

Incluso en un problema simple como éste, te estás moviendo desde los confines de lo que es tangible para el cerebro humano a una escala que está en cierto modo más allá de nuestra comprensión. Como seres finitos, podemos comprender el concepto de infinito o eternidad, pero nunca podemos experimentarlo realmente. Lo que significa que, a menudo, lo que sabemos que es cierto en nuestro mundo finito, resulta comportarse de forma diferente en un nivel infinito.

Aceptar la transición de unas matemáticas fácilmente descubribles y reproducibles a lo que sólo puede probarse e imaginarse en nuestras mentes forma parte de la belleza y la maravilla de las matemáticas.

Así que no tomes la lección de hoy al pie de la letra y te encojas de hombros.

Deja que haya una capa de niebla entre ti y la comprensión perfecta. Deja que tu mente se asombre por el hecho de que el infinito se comporta de forma extraña. Y deja que te haga desear más comprensión y, sobre todo, más matemáticas.

¡Gracias por leer y reflexionar sobre el infinito conmigo hoy!