Funciones o Mapeo

Ahora, en funciones o mapeo estudiaremos sobre un tipo especial de relaciones llamadas funciones o mapeo. Para entenderlas, tomemos algunos ejemplos de la vida real.

Todas estas preguntas tienen
respuestas únicas. Veamos
cómo podemos relacionar
esto en el aprendizaje de la cartografía.

● ¿Desde dónde sale el sol?

Este

● ¿Cuál es la capital de la India?

Delhi

● ¿Cuál es el sucesor de 4?

5

● ¿Cuál es la suma de 5 y 3?

8

Mapping o funciones:

Si A y B son dos conjuntos no vacíos, se dice que una relación ‘f’ del conjunto A al conjunto B es una función o mapping,
● Si cada elemento del conjunto A está asociado a un único elemento del conjunto B.

● La función ‘f’ de A a B se denota por f : A → B.

● Si f es una función de A a B y x ∈ A, entonces f(x) ∈ B donde f(x) se llama imagen de x bajo f y x se llama preimagen de f(x) bajo .

Nota:

Para que f sea un mapeo de A a B:

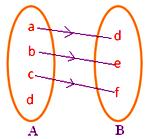
● Todo elemento de A debe tener imagen en B. La figura contigua no representa un mapeo ya que el elemento d del conjunto A no está asociado a ningún elemento del conjunto B.

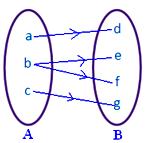
● Ningún elemento de A debe tener más de una imagen. La figura contigua no representa un mapeo ya que el elemento b del conjunto A está asociado a dos elementos d, f del conjunto B.

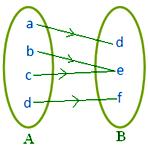
● Diferentes elementos de A pueden tener la misma imagen en B. La figura contigua representa un mapeo.

Nota:

Todo mapeo es una relación pero toda relación puede no ser un mapeo.

La función como tipo especial de relación:

Recordemos y revisemos la función como tipo especial de relación supongamos, que A y B son dos conjuntos no vacíos, entonces una regla ‘f’ que asocia cada elemento de A con un único elemento de B se llama función o mapeo de A a B.
Si ‘f’ es un mapeo de A a B,

lo expresamos como f: A → B

lo leemos como ‘f’ es una función de A a B.
Si ‘f ‘ es una función de A a B y x∈A e y∈B, entonces decimos que y es la imagen del elemento x bajo la función ‘ f ‘ y lo denotamos por f(x).
Por tanto, lo escribimos como y = f(x)

Aquí, el elemento x se llama la preimagen de y.

Así, para una función de A a B.
● A y B deben ser no vacíos.

● Cada elemento de A debe tener imagen en B.

● Ningún elemento de ‘A’ debe tener más de una imagen en ‘B’.
Nota:

● Dos o más elementos de A pueden tener la misma imagen en B.

● f : x → y significa que bajo la función de ‘f’ de A a B, un elemento x de A tiene imagen y en B.

● Es necesario que cada imagen de f esté en B pero puede haber algunos elementos en B que no sean imágenes f de ningún elemento de A.

● Relaciones y mapeo

Par ordenado

Producto cartesiano de dos conjuntos

Relación

Dominio y rango de una relación

Funciones o mapeo

Dominio Co-dominio y rango de una función

● Relaciones y mapeo – Hojas de trabajo

Hoja de trabajo sobre relación matemática

Hoja de trabajo sobre funciones o mapeo

.

Problemas de Matemáticas de 7º grado

Práctica de Matemáticas de 8º grado
Desde Funciones o Mapeo hasta PÁGINA DE INICIO