Circunferencia de un Círculo – Explicación y Ejemplos
On enero 21, 2022 by adminHemos visto antes cómo encontrar el perímetro del polígono. Sabemos que el círculo no es un polígono, por tanto, no debe tener perímetro. Usamos una forma equivalente para un círculo, llamada circunferencia.
En este artículo, vamos a discutir cómo encontrar la circunferencia de un círculo, la fórmula de la circunferencia del círculo y problemas de ejemplo sobre la circunferencia de un círculo.
¿Qué es la circunferencia de un círculo?
La distancia alrededor de un polígono como un cuadrado o rectángulo se llama el perímetro (P). En cambio, la distancia alrededor de un círculo se denomina circunferencia (C). Por lo tanto, la circunferencia de un círculo es la distancia lineal de un borde del círculo.
¿Por qué necesitamos calcular la circunferencia de un círculo?
Encontrar la circunferencia de un objeto es importante en los siguientes casos:
Si quieres comprar un sujetador, un pantalón o un jersey, necesitas saber la distancia alrededor de tu cintura o pecho. Aunque tu cuerpo no es un círculo perfecto, tendrás que medir su circunferencia con una cinta métrica. Los sastres utilizan sobre todo esta técnica para determinar la circunferencia de un vestido.
También necesitas saber la circunferencia de un círculo haciendo trabajos de manualidades, poniendo vallas alrededor de tu bañera de hidromasaje o simplemente resolviendo un problema de matemáticas para el colegio.
¿Cómo encontrar la circunferencia de un círculo?
Como se ha dicho antes, el perímetro o circunferencia de un círculo es la distancia alrededor de un círculo o de cualquier forma circular. La circunferencia de un círculo es la misma que la longitud de una línea recta que se dobla o se curva para formar el círculo. La circunferencia de un círculo se mide en metros, kilómetros, yardas, pulgadas, etc.
Hay dos formas de encontrar el perímetro o la circunferencia de un círculo. La primera fórmula consiste en utilizar el radio y la segunda en utilizar el diámetro de un círculo. Es importante tener en cuenta que, tanto los dos métodos dan el mismo resultado.
Vamos a echar un vistazo.
La circunferencia de un círculo viene dada por;
C = 2 * π* R = 2πR
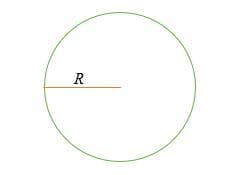
donde,
C = Circunferencia o perímetro,
R = el radio de un círculo,
π = la constante matemática conocida como Pi
O
C = π* D = π D
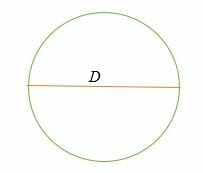
donde, D = 2R = El diámetro de un círculo
Para cualquier círculo, el cociente entre su circunferencia y su diámetro es igual a una constante conocida como pi.
Circunferencia/Diámetro = Pi
C /D = Pi o C/2R = pi
El valor aproximado de pi (π) = 22/7 = 3,1415926535897…. (un valor no terminal)
Para facilitar el cálculo de la circunferencia de un círculo, se toma el valor de pi como 3,14 (π = 3,14).
Veamos algunos ejemplos a continuación para pulir el concepto de circunferencia.
Ejemplo 1
Encuentra la circunferencia del círculo con un radio de 8 cm.
Solución
Circunferencia = 2 * π* R = 2πR
= 2 * 3,14 * 8
= 50,24 cm.
Ejemplo 2
Calcular la circunferencia de un círculo cuyo diámetro es de 70 mm
Solución
Circunferencia = π* D = π D
= 3,14 * 70
= 219.8 mm
Ejemplo 3
Calcular el perímetro de un jardín de flores circular cuyo radio es de 10 m.
Solución
Circunferencia = 2 * π* R = 2πR
= 2 * 3,14 * 10
= 62,8 m.
Ejemplo 4
La circunferencia de un círculo es de 440 metros. Halla el diámetro y el radio del círculo.
Solución
Circunferencia = 2 * π* R = 2πR
440 =2 * 3,14 * R
440 = 6.28R
Divide ambos lados por 6,28 para obtener,
R = 70,06
Por tanto, el radio del círculo es de 70,06 yardas. Pero, como el diámetro es el doble del radio de un círculo, entonces, el diámetro es igual a 140,12 yardas.
Ejemplo 5
El diámetro de las ruedas de una bicicleta es de 100 cm. Cuántas revoluciones dará cada rueda para recorrer una distancia de 157 metros
Solución
Calcular la circunferencia de la rueda de la bicicleta.
Circunferencia = π D
= 3.14 * 100
= 314 cm
Para obtener el número de revoluciones de la rueda, divide la distancia recorrida entre la circunferencia de la rueda.
Necesitamos convertir 157 metros a cm antes de dividir, así que multiplicamos 157 por 100 para obtener 15700 cm. Por tanto,
Número de revoluciones = 15700 cm/314 cm
= 50 revoluciones.
Ejemplo 6
Se corta un trozo de un alambre en forma de rectángulo de 100 cm de largo y 50 cm de ancho y se dobla para formar una circunferencia. Calcula la circunferencia y el radio del círculo formado.
Solución
La circunferencia del círculo formado = el perímetro del alambre rectangular.
Perímetro de un rectángulo = 2(L + W)
= 2(100 + 50) cm
= 2 * 150 cm
= 300 cm.
Por tanto, la circunferencia del círculo será de 300 cm.
Calcula ahora su radio.
Circunferencia = 2 π R
300 cm = 2 * π * R
300 cm = 2 * 3,14 * R
300 cm = 6,28R
Divide ambos lados por 6,28.
R = 47.77 cm
Por tanto, el radio del círculo será de 47,77 cm.
Ejemplo 7
El radio de cada rueda de una motocicleta es de 0,85 m. ¿Qué distancia recorrerá la motocicleta si cada rueda da 1000 vueltas? Supongamos que la motocicleta se mueve en línea recta.
Solución
En primer lugar, halla la circunferencia de la rueda.
Circunferencia = 2 π R
= 2 * 3,14 * 0,85
= 5,338 m.
Para hallar la distancia recorrida, multiplica la circunferencia de la rueda por el número de revoluciones tomadas.
Distancia = 5,338 * 1000
= 5338 m
Por tanto, la distancia recorrida es igual a 5,338 kilómetros.
Preguntas prácticas
- Se sirve una pizza de 12 pulgadas a Mike y sus amigos. Mike está interesado en calcular su circunferencia. Ayúdale
- El perímetro de un determinado cuadrado es 1/3 del área de un determinado círculo. Si la longitud del cuadrado es L unidades, determina el diámetro del círculo en términos de L.
Respuestas
- 12π pulgadas o 37,67 pulgadas
- 12L/π unidades
Deja una respuesta