2.12: Ecuación de Van der Waals

Una ecuación debida a Van der Waals amplía la ecuación de los gases ideales de forma sencilla. La ecuación de Van der Waals es

\Nque se ajusta a los datos de presión-volumen-temperatura de un gas real mejor que la ecuación del gas ideal. El ajuste mejorado se obtiene introduciendo dos parámetros (designados «\(a\)» y «\(b\)») que deben determinarse experimentalmente para cada gas. La ecuación de Van der Waals es particularmente útil en nuestro esfuerzo por comprender el comportamiento de los gases reales, porque encarna una imagen física simple para la diferencia entre un gas real y un gas ideal.

Al derivar la ley de Boyle a partir de las leyes de Newton, suponemos que las moléculas del gas no interactúan entre sí. Argumentos sencillos muestran que esto sólo puede ser aproximadamente cierto. Las moléculas de gas reales deben interactuar entre sí. A distancias cortas se repelen. A distancias algo mayores, se atraen. La ecuación del gas ideal también puede derivarse a partir de las suposiciones básicas que hacemos en §10 mediante una aplicación de la teoría de la termodinámica estadística. Haciendo diferentes suposiciones sobre las propiedades moleculares, podemos aplicar la termodinámica estadística para derivar({}^{5}\) la ecuación de van der Waals. Los supuestos necesarios son que las moléculas ocupan un volumen finito y que se atraen entre sí con una fuerza que varía como la inversa de una potencia de la distancia entre ellas. (Se suele suponer que la fuerza de atracción es proporcional a \(r^{-6}\).)

Para reconocer que las moléculas de los gases reales se atraen y se repelen, sólo tenemos que recordar que cualquier gas puede licuarse reduciendo su temperatura y aumentando la presión que se le aplica. Si enfriamos más el líquido, se congela hasta convertirse en un sólido. Ahora bien, dos características distintivas de un sólido son que conserva su forma y que es casi incompresible. Atribuimos la incompresibilidad de un sólido a las fuerzas de repulsión entre las moléculas que lo componen; se han acercado tanto unas a otras que las fuerzas de repulsión entre ellas se han vuelto importantes. Para comprimir el sólido, las moléculas deben acercarse aún más, lo que requiere una fuerza desmesurada. En cambio, si lanzamos un cubito de hielo al otro lado de la habitación, todas las moléculas de agua que lo componen vuelan juntas por la habitación. Evidentemente, las moléculas de agua del sólido se atraen entre sí, pues de lo contrario irían cada una por su lado: lanzar el cubito de hielo sería como lanzar un puñado de arena seca. Pero las moléculas de agua son las mismas moléculas sea cual sea la temperatura o la presión, por lo que si hay fuerzas de atracción y repulsión entre ellas en el sólido, estas fuerzas deben estar presentes también en las fases líquida y gaseosa.

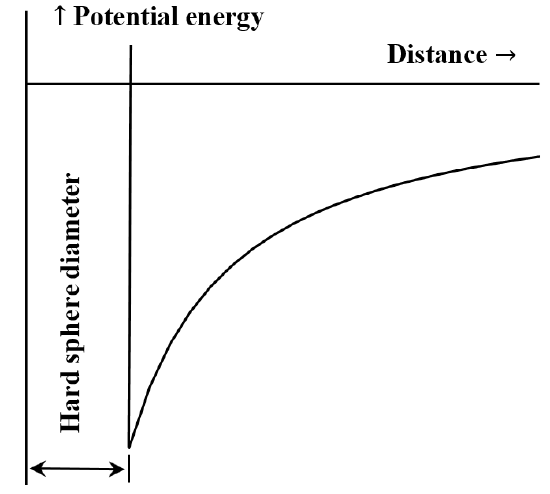
En la fase gaseosa, las moléculas están muy separadas; en la fase líquida o sólida, están empaquetadas. En su punto de ebullición, el volumen de un líquido es mucho menor que el del gas del que se condensa. En el punto de congelación, el volumen de un sólido sólo difiere ligeramente del volumen del líquido a partir del cual se congela, y es ciertamente mayor que cero. Estas observaciones comunes se explican fácilmente suponiendo que cualquier molécula tiene un volumen característico. Podemos entender esto, a su vez, como una consecuencia de la naturaleza de las fuerzas intermoleculares; evidentemente, estas fuerzas se hacen más fuertes a medida que disminuye la distancia entre un par de moléculas. Dado que un líquido o un sólido ocupan un volumen definido, la fuerza de repulsión debe aumentar más rápidamente que la fuerza de atracción cuando la distancia intermolecular es pequeña. A menudo es útil hablar del volumen molar de una fase condensada. Por volumen molar se entiende el volumen de un mol de una sustancia pura. El volumen molar de una fase condensada viene determinado por la distancia intermolecular en la que existe un equilibrio entre las fuerzas intermoleculares de atracción y repulsión.

Evidentemente las moléculas están muy cerca unas de otras en las fases condensadas. Si suponemos que los espacios vacíos entre las moléculas son despreciables, el volumen de una fase condensada es aproximadamente igual al número de moléculas de la muestra multiplicado por el volumen de una sola molécula. Entonces el volumen molar es el número de Avogadro por el volumen ocupado por una molécula. Si conocemos la densidad, D, y la masa molar, \(\overline{M}\), podemos encontrar el volumen molar, \(\overline{V}\), como

\

El volumen ocupado por una molécula, La presión y el volumen que aparecen en la ecuación de Van der Waals son la presión y el volumen del gas real. Podemos relacionar los términos de la ecuación de van der Waals con la ecuación del gas ideal: Resulta útil pensar en los términos \(\left(P+{an}^2}/{V^2}\right)\️ y \(\left(V-nb\right)\️ como la presión y el volumen de un hipotético gas ideal. Es decir

\Ndejamos la ecuación del gas ideal a partir de un modelo en el que las moléculas son masas puntuales que no interactúan. Así que el volumen de un gas ideal es el volumen ocupado por un gas cuyas moléculas individuales tienen volumen cero. Si las moléculas individuales de un gas real ocupan efectivamente un volumen \({b}/{overline{N}}), entonces \(n\) moles de ellas ocupan efectivamente un volumen

\

La ecuación de Van der Waals dice que el volumen de un gas real es el volumen que ocuparían las masas puntuales que no interactúan, \(V_{gas ideal}\), más el volumen efectivo de las propias moléculas del gas. (Cuando los datos de las moléculas de gas reales se ajustan a la ecuación de van der Waals, el valor de \(b\) suele ser algo mayor que el volumen estimado a partir de la densidad del líquido y el peso molecular. Véase el problema 24.)

De forma similar, tenemos

\Nque podemos entender esto como una consecuencia lógica de las interacciones atractivas entre las moléculas del gas real. Con \(a>0\), se dice que la presión del gas real es menor que la presión del gas ideal hipotético, en una cantidad que es proporcional a \({\left({n}/{V}\right)}^2\). La constante de proporcionalidad es \(a\). Dado que \({n}/{V}\\️) es la densidad molar (moles por unidad de volumen) de las moléculas del gas, es una medida de la concentración. El número de colisiones entre moléculas del mismo tipo es proporcional al cuadrado de su concentración. (Consideramos este punto con más detalle en los Capítulos 4 y 5.) Así que \ {\left({n}/{V}\right)}^2 es una medida de la frecuencia con la que las moléculas reales del gas entran en contacto entre sí. Si se atraen cuando se acercan unas a otras, el efecto de esta atracción debería ser proporcional a \({\left({n}/{V}\right)}^2). Así que la ecuación de van der Waals es consistente con la idea de que la presión de un gas real es diferente de la presión del gas ideal hipotético en una cantidad que es proporcional a la frecuencia y la fuerza de las interacciones atractivas.

¿Pero por qué las interacciones atractivas deberían tener este efecto; por qué la presión del gas real debería ser menor que la del gas ideal hipotético? Quizás la mejor manera de desarrollar una imagen cualitativa es reconocer que las fuerzas intermoleculares atractivas tienden a hacer que las moléculas del gas se agrupen. Al fin y al cabo, son estas fuerzas atractivas las que hacen que las moléculas se aglutinen en un líquido a bajas temperaturas. Por encima del punto de ebullición, la capacidad de las moléculas del gas de ir por caminos separados limita los efectos de esta tendencia; sin embargo, incluso en el gas, las fuerzas atractivas deben actuar de forma que tiendan a reducir el volumen ocupado por las moléculas. Dado que el volumen ocupado por el gas viene dictado por el tamaño del recipiente -y no por las propiedades del propio gas-, esta tendencia a la aglomeración se expresa como una disminución de la presión.