E se os seus dados NÃO forem normais?

Introdução

Esta é a semana de Halloween, e entre os truques e os presentes, nós, cromos dos dados, estamos rindo sobre este lindo meme sobre as mídias sociais.

Achas que isto é uma piada? Deixa-me dizer-te, isto não é uma brincadeira. É assustador, fiel ao espírito do Halloween!

Se não podemos assumir que a maioria dos nossos dados (de origem empresarial, social, económica ou científica) são pelo menos aproximadamente ‘Normais’ (ou seja, são gerados por um processo Gaussiano ou por uma soma de múltiplos processos deste tipo), então estamos condenados!

Existe uma lista extremamente breve de coisas que não serão válidas,

• Todo o conceito de seis-sigma
• A famosa regra 68-9595-99.7
• O conceito ‘santo’ de p=0,05 (vem de intervalo 2 sigma) em análise estatística

Suficientemente escolar? Vamos falar mais sobre isso…

A Distribuição Normal Onipotente e Onipresente

Vamos manter esta seção curta e doce.

A distribuição Normal (Gaussiana) é a distribuição de probabilidade mais amplamente conhecida. Aqui estão alguns links para os artigos descrevendo seu poder e ampla aplicabilidade,

• Por que os cientistas de dados amam Gaussiano

• Como dominar a porção estatística de sua entrevista de dados científicos
• O que é tão importante sobre a distribuição normal?

Devido ao seu aparecimento em vários domínios e ao Teorema do Limite Central (CLT), esta distribuição ocupa um lugar central na ciência e análise de dados.

Então, qual é o problema?

>

Esta é toda a hunky-dory, qual é o problema?

O problema é que muitas vezes você pode encontrar uma distribuição para seu conjunto de dados específico, que pode não satisfazer a Normalidade, ou seja, as propriedades de uma distribuição Normal. Mas devido à dependência excessiva na suposição da Normalidade, a maioria das estruturas analíticas de negócios são feitas sob medida para trabalhar com conjuntos de dados normalmente distribuídos.

Está quase entranhada em nosso subconsciente.

Vamos dizer que você é solicitado a detectar se um novo lote de dados de algum processo (engenharia ou negócios) faz sentido. Por ‘fazer sentido’, você quer dizer se os novos dados pertencem, ou seja, se estão dentro do ‘intervalo esperado’.

O que é essa ‘expectativa’? Como quantificar o intervalo?

Automaticamente, como se fosse dirigido por uma unidade subconsciente, medimos a média e o desvio padrão do conjunto de dados da amostra e procedemos para verificar se os novos dados estão dentro de certos desvios padrão.

Se tivermos de trabalhar com um limite de confiança de 95%, então ficamos felizes em ver os dados dentro de 2 desvios padrão. Se precisarmos de um limite mais estrito, verificamos 3 ou 4 desvios padrão. Nós calculamos Cpk, ou seguimos as diretrizes de seis siglas para ppm (partes por milhão) de qualidade.

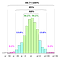
Todos estes cálculos são baseados na suposição implícita de que os dados da população (NÃO a amostra) seguem a distribuição gaussiana i.e. o processo fundamental, a partir do qual todos os dados foram gerados (no passado e no presente), é governado pelo padrão do lado esquerdo.

Mas o que acontece se os dados seguem o padrão do lado direito?

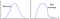
Or, isto, e… aquilo?

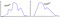
Existe um limite mais universal quando os dados NÃO são normais?

No final do dia, ainda precisaremos de uma técnica matematicamente sólida para quantificar nosso limite de confiança, mesmo que os dados não sejam normais. Isso significa que nosso cálculo pode mudar um pouco, mas ainda assim devemos ser capazes de dizer algo como isto-

“A probabilidade de observar um novo ponto de dados a uma certa distância da média é tal e tal…”

Obviamente, precisamos buscar um limite mais universal do que os queridos limites gaussianos de 68-95-99.7 (correspondendo a 1/2/3 de distância padrão de desvios da média).

Felizmente, existe um tal limite chamado “Chebyshev Bound”.

O que é Chebyshev Bound e como é útil?

A desigualdade de Chebyshev (também chamada de desigualdade Bienaymé-Chebyshev) garante que, para uma ampla classe de distribuições de probabilidade, não mais do que uma certa fração de valores pode estar a mais do que uma certa distância da média.

Especificamente, não mais que 1/k² dos valores da distribuição podem estar a mais de k desvios padrão da média (ou equivalentemente, pelo menos 1-1/k² dos valores da distribuição estão dentro de k desvios padrão da média).

Aplica-se a tipos virtualmente ilimitados de distribuições de probabilidade e funciona numa hipótese muito mais relaxada do que a Normalidade.

Como funciona?

Se você não sabe nada sobre o processo secreto por trás dos seus dados, há uma boa chance de você poder dizer o seguinte,

“Estou confiante que 75% de todos os dados devem estar dentro de 2 desvios padrão de distância da média”,

Or,

Estou confiante que 89% de todos os dados devem estar dentro de 3 desvios padrão de distância da média”.

Aqui é o que parece para uma distribuição com aspecto arbitrário,

Como aplicá-lo?

Como você já pode adivinhar, a mecânica básica da sua análise de dados não precisa mudar um pouco. Você ainda irá reunir uma amostra dos dados (quanto maior, melhor), calcular as mesmas duas quantidades que você está acostumado a calcular – média e desvio padrão, e então aplicar os novos limites ao invés da regra 68-95-99.7.

A tabela tem a seguinte aparência (aqui k denota que muitos desvios-padrão afastam-se da média),

Está aqui uma demonstração em vídeo da sua aplicação,

Qual é a captura? Porque é que as pessoas não usam este limite ‘mais universal’?

É óbvio qual é o senão olhando para a tabela ou para a definição matemática. A regra Chebyshev é muito mais fraca do que a regra Gaussiana na questão de colocar limites nos dados.

Segue um padrão de 1/k² em comparação com um padrão de queda exponencial para a distribuição Normal.

Por exemplo, para limitar qualquer coisa com 95% de confiança, você precisa incluir dados de até 4,5 desvios padrão vs. Apenas 2 desvios padrão (para Normal).

Mas ainda pode salvar o dia quando os dados não se parecem nada com uma distribuição Normal.

Existe algo melhor?

Existe outro limite chamado, “Chernoff Bound”/Hoeffding inequality que dá uma distribuição de cauda exponencialmente acentuada (em comparação com os 1/k²) para somas de variáveis aleatórias independentes.

Isso também pode ser usado no lugar da distribuição Gaussiana quando os dados não parecem normais, mas apenas quando temos um alto grau de confiança de que o processo subjacente é composto de subprocessos que são completamente independentes uns dos outros.

Felizmente, em muitos casos sociais e empresariais, os dados finais são o resultado de uma interação extremamente complicada de muitos subprocessos que podem ter forte interdependência.

Sumário

Neste artigo, aprendemos sobre um tipo particular de vinculação estatística que pode ser aplicada à mais ampla distribuição possível de dados, independente da suposição da Normalidade. Isto vem a calhar quando sabemos muito pouco sobre a verdadeira fonte dos dados e não podemos assumir que segue uma distribuição Gaussiana. O limite segue uma lei de poder ao invés de uma natureza exponencial (como Gaussiano) e, portanto, é mais fraco. Mas é uma ferramenta importante a ter em seu repertório para analisar qualquer tipo arbitrário de distribuição de dados.