Was ist, wenn Ihre Daten NICHT normal sind?

Einführung

Es ist Halloween-Woche, und zwischen den Süßigkeiten kichern wir Datenfreaks über dieses niedliche Meme in den sozialen Medien.

Sie halten das für einen Scherz? Lassen Sie mich Ihnen sagen, dass dies nicht zum Lachen ist. Es ist gruselig, getreu dem Geist von Halloween!

Wenn wir nicht davon ausgehen können, dass die meisten unserer Daten (geschäftlicher, sozialer, wirtschaftlicher oder wissenschaftlicher Art) zumindest annähernd „normal“ sind (d.h. sie werden durch einen Gauß-Prozess oder durch eine Summe mehrerer solcher Prozesse erzeugt), dann sind wir dem Untergang geweiht!

Hier ist eine extrem kurze Liste von Dingen, die nicht gültig sind,

• Das ganze Konzept von Six-Sigma
• Die berühmte 68-95-99,7 Regel
• Das ‚heilige‘ Konzept von p=0,05 (kommt vom 2-Sigma-Intervall) in der statistischen Analyse

Schrecklich genug? Lassen Sie uns mehr darüber reden…

Die allmächtige und allgegenwärtige Normalverteilung

Lassen Sie uns diesen Abschnitt kurz und bündig halten.

Die Normalverteilung (Gaußverteilung) ist die bekannteste Wahrscheinlichkeitsverteilung. Hier sind einige Links zu Artikeln, die ihre Leistungsfähigkeit und breite Anwendbarkeit beschreiben,

• Warum Datenwissenschaftler die Gaußverteilung lieben

• Wie Sie den Statistikteil Ihres Data Science-Interviews dominieren
• Was ist so wichtig an der Normalverteilung?

Aufgrund ihres Auftretens in verschiedenen Bereichen und des zentralen Grenzwertsatzes (CLT) nimmt diese Verteilung einen zentralen Platz in der Datenwissenschaft und -analyse ein.

Wo liegt also das Problem?

Das ist ja alles schön und gut, wo ist das Problem?

Das Problem ist, dass man oft eine Verteilung für einen bestimmten Datensatz findet, die nicht die Normalität, d.h. die Eigenschaften einer Normalverteilung, erfüllt. Aufgrund der übermäßigen Abhängigkeit von der Normalitätsannahme sind die meisten Business-Analytics-Frameworks jedoch auf die Arbeit mit normalverteilten Datensätzen zugeschnitten.

Sie ist fast schon in unserem Unterbewusstsein verankert.

Angenommen, Sie werden gebeten zu prüfen, ob ein neuer Datenstapel aus einem bestimmten Prozess (technisch oder geschäftlich) sinnvoll ist. Mit „sinnvoll“ meinen Sie, ob die neuen Daten dazugehören, d.h. ob sie im „erwarteten Bereich“ liegen.

Was ist diese „Erwartung“? Wie lässt sich der Bereich quantifizieren?

Automatisch, wie von einem unterbewussten Antrieb gesteuert, messen wir den Mittelwert und die Standardabweichung des Stichprobendatensatzes und prüfen dann, ob die neuen Daten in einen bestimmten Standardabweichungsbereich fallen.

Wenn wir mit einer Konfidenzgrenze von 95 % arbeiten müssen, sind wir froh, wenn die Daten innerhalb von 2 Standardabweichungen liegen. Wenn wir eine strengere Grenze brauchen, prüfen wir 3 oder 4 Standardabweichungen. Wir berechnen Cpk oder folgen den Six-Sigma-Richtlinien für das Qualitätsniveau ppm (parts-per-million).

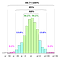
Alle diese Berechnungen beruhen auf der impliziten Annahme, dass die Daten der Grundgesamtheit (NICHT der Stichprobe) der Gauß-Verteilung folgen, d. h.d. h. der grundlegende Prozess, aus dem alle Daten (in der Vergangenheit und in der Gegenwart) hervorgegangen sind, wird durch das Muster auf der linken Seite bestimmt.

Aber was passiert, wenn die Daten dem Muster auf der rechten Seite folgen?

Oder, dies, und… das?

Gibt es eine allgemeingültigere Schranke, wenn die Daten NICHT normal sind?

Am Ende brauchen wir immer noch eine mathematisch solide Technik, um unsere Konfidenzschranke zu quantifizieren, auch wenn die Daten nicht normal sind. Das heißt, unsere Berechnung kann sich ein wenig ändern, aber wir sollten immer noch in der Lage sein, so etwas zu sagen wie:

„Die Wahrscheinlichkeit, einen neuen Datenpunkt in einem bestimmten Abstand vom Durchschnitt zu beobachten, ist so und so groß…“

Es ist offensichtlich, dass wir eine universellere Schranke suchen müssen als die geschätzten Gaußschen Schranken von 68-95-99.7 (entsprechend 1/2/3 Standardabweichungen vom Mittelwert).

Glücklicherweise gibt es eine solche Schranke, die „Tschebyscheff-Schranke“.

Was ist die Tschebyscheff-Schranke und wie ist sie nützlich?

Die Tschebyscheff-Ungleichung (auch Bienaymé-Tschebyscheff-Ungleichung genannt) garantiert, dass für eine breite Klasse von Wahrscheinlichkeitsverteilungen nicht mehr als ein bestimmter Bruchteil der Werte mehr als einen bestimmten Abstand vom Mittelwert haben kann.

Konkret bedeutet dies, dass nicht mehr als 1/k² der Werte der Verteilung mehr als k Standardabweichungen vom Mittelwert entfernt sein können (oder äquivalent dazu, dass mindestens 1-1/k² der Werte der Verteilung innerhalb von k Standardabweichungen vom Mittelwert liegen).

Sie ist auf praktisch unbegrenzte Arten von Wahrscheinlichkeitsverteilungen anwendbar und funktioniert unter einer viel lockereren Annahme als die Normalität.

Wie funktioniert sie?

Selbst wenn Sie nichts über den geheimen Prozess hinter Ihren Daten wissen, ist die Wahrscheinlichkeit groß, dass Sie Folgendes sagen können:

„Ich bin zuversichtlich, dass 75 % aller Daten innerhalb von 2 Standardabweichungen vom Mittelwert liegen sollten“,

oder,

„Ich bin zuversichtlich, dass 89 % aller Daten innerhalb von 3 Standardabweichungen vom Mittelwert liegen sollten“.

So sieht es für eine beliebig aussehende Verteilung aus,

Wie kann man es anwenden?

Wie Sie sich inzwischen denken können, muss sich an der grundlegenden Mechanik Ihrer Datenanalyse nichts ändern. Sie werden immer noch eine Stichprobe der Daten nehmen (je größer, desto besser), die gleichen beiden Größen berechnen, die Sie gewohnt sind zu berechnen – Mittelwert und Standardabweichung – und dann die neuen Grenzen anstelle der 68-95-99,7-Regel anwenden.

Die Tabelle sieht wie folgt aus (hier bedeutet k so viele Standardabweichungen vom Mittelwert entfernt),

Eine Video-Demo der Anwendung ist hier,

Wo ist der Haken?

Der Haken ist offensichtlich, wenn man sich die Tabelle oder die mathematische Definition ansieht. Die Tschebyscheff-Regel ist viel schwächer als die Gauß-Regel, wenn es darum geht, die Daten einzugrenzen.

Sie folgt einem 1/k²-Muster im Vergleich zu einem exponentiell fallenden Muster für die Normalverteilung.

Um zum Beispiel irgendetwas mit 95%iger Sicherheit einzugrenzen, müssen Sie Daten bis zu 4,5 Standardabweichungen einbeziehen. Nur 2 Standardabweichungen (für die Normalverteilung).

Aber es kann immer noch den Tag retten, wenn die Daten nicht wie eine Normalverteilung aussehen.

Gibt es etwas Besseres?

Es gibt eine weitere Schranke, die „Chernoff-Schranke“/Hoeffding-Ungleichung, die eine exponentiell scharfe Schwanzverteilung (im Vergleich zu 1/k²) für Summen unabhängiger Zufallsvariablen ergibt.

Sie kann auch anstelle der Gauß-Verteilung verwendet werden, wenn die Daten nicht normal aussehen, aber nur, wenn wir ein hohes Maß an Vertrauen haben, dass der zugrunde liegende Prozess aus Teilprozessen besteht, die völlig unabhängig voneinander sind.

Unglücklicherweise sind in vielen sozialen und geschäftlichen Fällen die endgültigen Daten das Ergebnis einer äußerst komplizierten Interaktion vieler Teilprozesse, die stark voneinander abhängig sein können.

Zusammenfassung

In diesem Artikel haben wir eine besondere Art von statistischer Schranke kennengelernt, die unabhängig von der Annahme der Normalität auf die größtmögliche Verteilung von Daten angewendet werden kann. Dies ist nützlich, wenn wir sehr wenig über die wahre Quelle der Daten wissen und nicht davon ausgehen können, dass sie einer Gaußschen Verteilung folgen. Die Schranke folgt einem Potenzgesetz anstelle einer Exponentialverteilung (wie Gauß) und ist daher schwächer. Sie ist jedoch ein wichtiges Hilfsmittel für die Analyse jeder beliebigen Datenverteilung.