Warum ist 0,999… gleich 1?

Eine andere Art, über die Terme in unserer Summation nachzudenken, ist, dass jeder aufeinanderfolgende Term durch Multiplikation des vorherigen Terms mit einem gemeinsamen Verhältnis erhalten wird.

Das bedeutet, dass wir eine geometrische Reihe haben, die zu a/(1 – r) konvergiert, wobei a der erste Wert in der Reihe ist und r das Verhältnis ist, mit dem wir multiplizieren, um den nächsten Term zu erhalten.

Konvergenz in einer Reihe bedeutet einfach, dass die Reihe sich einem bestimmten Wert immer weiter annähert, wenn man immer mehr Terme zur Reihe hinzufügt. Die Reihe nähert sich dem Konvergenzwert unendlich stark an. Auf einer unendlichen Skala wird die Konvergenz zur Gleichheit.

In unserem Fall beginnen wir mit 1/10 und multiplizieren jedes Mal mit 1/10, also sind sowohl a als auch r = 1/10.

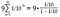
Vervollständigen Sie die Arithmetik auf der rechten Seite.

Jetzt haben wir formal gezeigt, dass 0.999… gegen 1 konvergiert oder gleich 1 ist.

Abschließende Gedanken &Inspiration

Wenn sich das für Sie seltsam anfühlt, ist das gut! Du weißt, dass zwei verschiedene Zahlen eigentlich verschiedene Zahlen sein sollten. Die kontraintuitive Natur dieses Problems ist Teil der Seltsamkeit, die mit der Arbeit mit der Unendlichkeit einhergeht.

Selbst bei einem einfachen Problem wie diesem bewegt man sich von den Grenzen dessen, was für das menschliche Gehirn greifbar ist, auf eine Ebene, die in gewisser Weise jenseits unseres Verständnisses liegt. Als endliche Wesen können wir das Konzept der Unendlichkeit oder der Ewigkeit begreifen, aber wir können es nie wirklich erfahren. Das bedeutet, dass das, was wir in unserer endlichen Welt für wahr halten, sich auf einer unendlichen Ebene oft anders verhält.

Das Akzeptieren des Übergangs von der leicht zu entdeckenden und reproduzierbaren Mathematik zu dem, was wir nur in unseren Köpfen testen und uns vorstellen können, ist Teil der Schönheit und des Wunders der Mathematik.

Nehmen Sie die heutige Lektion also nicht für bare Münze und schieben Sie sie beiseite.

Lassen Sie eine Nebelschicht zwischen sich und dem vollkommenen Verständnis liegen. Lass dich von der Tatsache verwirren, dass sich die Unendlichkeit seltsam verhält. Und lass es dich nach mehr Verständnis und vor allem nach mehr Mathematik verlangen.

Danke, dass du heute mit mir über die Unendlichkeit nachgedacht hast!