Umfang eines Kreises – Erklärung und Beispiele
On Januar 21, 2022 by adminWir haben schon gesehen, wie man den Umfang eines Polygons findet. Wir wissen, dass ein Kreis kein Polygon ist und daher auch keinen Umfang haben sollte. Wir verwenden eine äquivalente Form für einen Kreis, die als Umfang bezeichnet wird.
In diesem Artikel werden wir besprechen, wie man den Umfang eines Kreises findet, die Formel für den Umfang eines Kreises und Beispielprobleme zum Umfang eines Kreises.
Was ist der Umfang eines Kreises?
Der Abstand um ein Polygon wie ein Quadrat oder Rechteck wird als Umfang (P) bezeichnet. Die Strecke um einen Kreis hingegen wird als Umfang (C) bezeichnet. Der Umfang eines Kreises ist also der lineare Abstand einer Kante des Kreises.
Warum müssen wir den Umfang eines Kreises berechnen?
Die Bestimmung des Umfangs eines Objekts ist in folgenden Fällen wichtig:
Ob Sie einen BH, eine Hose oder einen Pullover kaufen wollen, müssen Sie den Abstand um Ihre Taille oder Brust wissen. Auch wenn dein Körper kein perfekter Kreis ist, musst du seinen Umfang mit einem Maßband messen. Schneider verwenden diese Technik meist, um den Umfang eines Kleides zu bestimmen.
Den Umfang eines Kreises musst du auch wissen, wenn du handwerkliche Arbeiten ausführst, einen Zaun um deinen Whirlpool anbringst oder einfach nur eine Matheaufgabe für die Schule löst.
Wie findet man den Umfang eines Kreises?
Wie bereits erwähnt, ist der Umfang eines Kreises der Abstand um einen Kreis oder eine beliebige Kreisform. Der Umfang eines Kreises ist gleich der Länge einer geraden Linie, die gefaltet oder gebogen wird, um den Kreis zu bilden. Der Umfang eines Kreises wird in Metern, Kilometern, Yards, Zoll usw. gemessen.
Es gibt zwei Möglichkeiten, den Umfang eines Kreises zu bestimmen. Bei der ersten Formel wird der Radius verwendet, bei der zweiten der Durchmesser eines Kreises. Es ist wichtig zu beachten, dass beide Methoden das gleiche Ergebnis liefern.
Lassen Sie uns einen Blick darauf werfen.
Der Umfang eines Kreises ist gegeben durch;
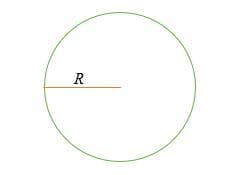
C = 2 * π* R = 2πR
wobei,
C = Umfang oder Perimeter,
R = der Radius eines Kreises,
π = die mathematische Konstante Pi
oder
C = π* D = π D
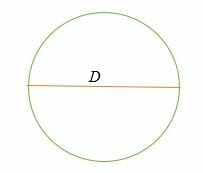
wobei, D = 2R = der Durchmesser eines Kreises
Für jeden Kreis ist das Verhältnis seines Umfangs zu seinem Durchmesser gleich einer Konstante, bekannt als Pi.
Umfang/Durchmesser = Pi
C /D = Pi oder C/2R = pi
Der ungefähre Wert von pi (π) = 22/7 = 3,1415926535897…. (ein nicht endlicher Wert)
Zur einfacheren Berechnung des Umfangs eines Kreises wird der Wert von pi mit 3,14 (π = 3,14) angenommen.
Lassen Sie uns im Folgenden einige Beispiele sehen, um das Konzept des Umfangs zu verdeutlichen.
Beispiel 1
Bestimme den Umfang des Kreises mit einem Radius von 8 cm.
Lösung
Umfang = 2 * π* R = 2πR
= 2 * 3,14 * 8
= 50,24 cm.
Beispiel 2
Berechnen Sie den Umfang eines Kreises, dessen Durchmesser 70 mm beträgt
Lösung
Umfang = π* D = π D
= 3,14 * 70
= 219.8 mm
Beispiel 3
Berechnen Sie den Umfang eines kreisförmigen Blumengartens, dessen Radius 10 m beträgt.
Lösung
Umfang = 2 * π* R = 2πR
= 2 * 3,14 * 10
= 62,8 m.
Beispiel 4
Der Umfang eines Kreises beträgt 440 m. Finde den Durchmesser und den Radius des Kreises.
Lösung
Umfang = 2 * π* R = 2πR
440 =2 * 3,14 * R
440 = 6.28R
Dividieren Sie beide Seiten durch 6,28 und Sie erhalten,
R = 70,06
Der Radius des Kreises beträgt also 70,06 Meter. Da aber der Durchmesser das Doppelte des Radius eines Kreises ist, ist der Durchmesser gleich 140,12 m.
Beispiel 5
Der Durchmesser der Räder eines Fahrrads beträgt 100 cm. Wie viele Umdrehungen macht jedes Rad, um eine Strecke von 157 Metern zurückzulegen
Lösung
Berechnen Sie den Umfang des Fahrrads.
Umfang = π D
= 3.14 * 100
= 314 cm
Um die Anzahl der Umdrehungen des Rades zu erhalten, teilt man die zurückgelegte Strecke durch den Umfang des Rades.
Wir müssen 157 Meter in cm umrechnen, bevor wir dividieren, also multiplizieren wir 157 mit 100, um 15700 cm zu erhalten. Also,
Anzahl der Umdrehungen = 15700 cm/314 cm
= 50 Umdrehungen.
Beispiel 6
Ein Stück Draht in Form eines Rechtecks von 100 cm Länge und 50 cm Breite wird geschnitten und zu einem Kreis gefaltet. Berechne den Umfang und den Radius des gebildeten Kreises.
Lösung
Der Umfang des gebildeten Kreises = der Umfang des rechteckigen Drahtes.
Perimeter eines Rechtecks = 2(L + B)
= 2(100 + 50) cm
= 2 * 150 cm
= 300 cm.
Der Umfang des Kreises beträgt also 300 cm.
Berechne nun seinen Radius.
Umfang = 2 π R
300 cm = 2 * π * R
300 cm = 2 * 3,14 * R
300 cm = 6,28R
Dividiere beide Seiten durch 6,28.
R = 47.77 cm
Der Radius des Kreises beträgt also 47,77 cm.
Beispiel 7
Der Radius jedes Rades eines Motorrades beträgt 0,85 m. Wie weit fährt das Motorrad, wenn jedes Rad 1000 Umdrehungen macht. Angenommen, das Motorrad bewegt sich auf einer geraden Linie.
Lösung
Ermitteln Sie zunächst den Umfang des Rades.
Umfang = 2 π R
= 2 * 3,14 * 0,85
= 5,338 m.
Um die zurückgelegte Strecke zu ermitteln, multiplizieren Sie den Umfang des Rades mit der Anzahl der Umdrehungen.
Entfernung = 5,338 * 1000
= 5338 m
Die zurückgelegte Entfernung ist also gleich 5,338 Kilometer.
Praxisfragen
- Eine 12-Zoll-Pizza wird Mike und seinen Freunden serviert. Mike ist daran interessiert, den Umfang zu berechnen. Hilf ihm!
- Der Umfang eines bestimmten Quadrats ist 1/3 der Fläche eines bestimmten Kreises. Wenn die Länge des Quadrats L Einheiten ist, bestimme den Durchmesser des Kreises in Bezug auf L.
Antworten
- 12π Zoll oder 37,67 Zoll
- 12L/π Einheiten
Schreibe einen Kommentar