Articles

Produktsumme (SOP) & Summenprodukt (POS)

On November 10, 2021 by admin

Summenprodukt (POS) & Produktsumme (SOP)

Produktsumme (SOP)

Produktsumme ist die abgekürzte Form von SOP. Die Produktsummenform ist eine Ausdrucksform in der Booleschen Algebra, bei der verschiedene Produktterme von Eingaben summiert werden. Dieses Produkt ist keine arithmetische Multiplikation, sondern eine boolesche logische UND-Verknüpfung und die Summe ist eine boolesche logische ODER-Verknüpfung.

Um die SOP besser zu verstehen, müssen wir den Min-Term kennen.

Min-Term

Minterm ist der Term, der für eine minimale Anzahl von Kombinationen von Eingaben wahr ist. Das heißt, er ist nur für eine einzige Kombination von Eingängen wahr.

Da das UND-Gatter auch nur dann wahr ist, wenn alle seine Eingänge wahr sind, können wir sagen, dass Min-Terme UND von Eingangskombinationen sind, wie in der folgenden Tabelle.

3 Eingänge haben 8 verschiedene Kombinationen. Jede Kombination hat einen Min-Term, der durch ein kleines m gekennzeichnet ist und dessen dezimale Kombinationsnummer tiefgestellt ist. Jeder dieser Min-Terme ist nur für die spezifische Eingangskombination wahr.

• Sie können auch lesen: Digitaler asynchroner Zähler (Rundungszähler) – Typen, Arbeitsweise & Anwendung

Arten von Summenformen (SOP)

Es gibt einige verschiedene Formen von Summenprodukten.

• Kanonische SOP-Form
• Nichtkanonische SOP-Form
• Minimale SOP-Form

Kanonische SOP-Form

Dies ist die Standardform der Summe des Produkts. Sie wird durch O Ring der Minima der Funktion gebildet, für die die Ausgabe wahr ist. Sie wird auch als Summe der Min-Terme oder kanonische disjunktive Normalform (CDNF) bezeichnet. Das ist nur ein schicker Name. „Kanonisch“ bedeutet „standardisiert“ und „disjunktiv“ bedeutet „logische ODER-Verknüpfung“.

Der kanonische SOP-Ausdruck wird durch das Summenzeichen ∑ und die Min-Terme in den geschweiften Klammern dargestellt, für die die Ausgabe wahr ist.

Die Wahrheitstabelle einer Funktion ist zum Beispiel unten angegeben.

Für diese Funktion lautet der kanonische SOP-Ausdruck

F = ∑( m1, m2, m3, m5 )

Das bedeutet, dass die Funktion für die Minterme {1, 2, 3, 5} wahr ist.

Durch Erweiterung der Summation erhalten wir.

F = m1 + m2 + m3 + m5

Nun setzen wir die Min-Terme in den Ausdruck ein

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

Die kanonische Form enthält alle Eingänge entweder komplementiert oder nicht komplementiert in ihren Produkttermen.

Sie können auch lesen: Digitaler Synchronzähler – Typen, Funktionsweise & Anwendungen

Nicht-kanonische SOP-Form

Wie der Name schon sagt, ist diese Form die nicht-standardisierte Form von SOP-Ausdrücken. Die Produktterme sind nicht die Mindestterme, aber sie sind vereinfacht. Nehmen wir die obige Funktion in kanonischer Form als Beispiel.

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = A̅B̅C + A̅B(C̅ + C) + AB̅C

F = A̅B̅C + A̅B(1) + AB̅C

F = A̅B̅C + A̅B + AB̅C

Dieser Ausdruck ist immer noch in der Summenform des Produkts, aber er ist nichtkanonische oder nicht standardisierte Form.

Minimale SOP-Form

Diese Form ist der am meisten vereinfachte SOP-Ausdruck einer Funktion. Sie ist auch eine Form der nicht-kanonischen Form. Die minimale SOP-Form kann mit Hilfe von Theoremen der Booleschen Algebra erstellt werden, aber sie ist sehr einfach mit Hilfe der Karnaugh-Map (K-Map) zu erstellen.

Die minimale SOP-Form wird bevorzugt, weil sie eine minimale Anzahl von Gattern und Eingabeleitungen verwendet. Sie ist wegen ihrer kompakten Größe, ihrer hohen Geschwindigkeit und ihrer niedrigen Herstellungskosten kommerziell vorteilhaft.

Lassen Sie uns ein Beispiel für die oben genannte Funktion in kanonischer Form nehmen.

Ihre K-Map ist unten angegeben.

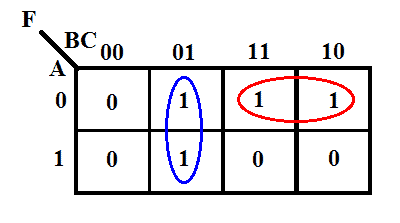
Gemäß der K-Map lautet der Ausgangsausdruck

F = B̅C + A̅B

Dies ist der vereinfachte &optimierte Ausdruck für die genannte Funktion. Dieser Ausdruck benötigt nur zwei UND-Gatter mit 2 Eingängen & und ein ODER-Gatter mit 2 Eingängen. Die kanonische Form benötigt jedoch vier UND-Gatter mit 3 Eingängen & ein ODER-Gatter mit 4 Eingängen, was relativ kostspieliger ist als die Implementierung der Minimalform.

• Sie können auch lesen: Ringzähler & Johnson-Zähler – Aufbau & Funktionsweise

Schematischer Entwurf eines Summenprodukts (SOP)

Der SOP-Ausdruck implementiert ein zweistufiges UND-ODER-Design, bei dem das Gatter der ersten Stufe ein UND-Gatter ist und das Gatter der zweiten Stufe ein ODER-Gatter ist. Schematischer Entwurf des SOP-Ausdrucks benötigt eine Gruppenanordnung von UND-Gattern & ein ODER-Gatter.

Jeder SOP-Ausdruck hat in etwa den gleichen Entwurf, d.h. alle Eingänge gehen durch ein UND-Gatter und dann fließt der Ausgang dieser UND-Gatter durch ein ODER-Gatter, wie in der nachstehenden Abbildung gezeigt.

Die Anzahl der Eingänge und die Anzahl der UND-Gatter hängt vom Ausdruck ab, den man implementiert.

Ein Beispiel für den Entwurf eines kanonischen und eines minimalen SOP-Ausdrucks für eine Funktion ist unten angegeben.

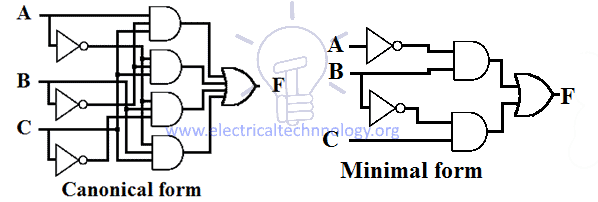
Umwandlung von der minimalen SOP in die kanonische SOP-Form

Die Umwandlung von der minimalen oder einer beliebigen nicht-kanonischen Form in die kanonische Form ist sehr einfach.

Wie wir wissen, hat die kanonische Form minimale Terme & Die minimalen Terme bestehen aus allen Eingängen, die entweder komplementiert oder nicht komplementiert sind. Wir multiplizieren also jeden Term der minimalen SOP mit der Summe der komplementären und nicht-komplementären Form der fehlenden Eingaben. Ein Beispiel für die Umwandlung der obigen Funktion in die minimale SOP-Form ist unten angegeben.

Minimale SOP-Form

F = A̅B + B̅C

Dem Term A̅B fehlt die Eingabe C. Wir multiplizieren also A̅B mit (C+C̅), weil (C+C̅ = 1). Dem Term B̅C fehlt der Eingang A. Er wird also mit (A+A̅)

F = A̅B(C + C̅) + B̅C(A + A̅)

F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C

Dieser Ausdruck ist nun in kanonischer Form.

Umwandlung von kanonischer SOP in kanonische POS

Standard-SOP-Ausdrücke können in Standard-POS-Ausdrücke (Summenprodukt) umgewandelt werden. Zum Beispiel hat die oben angegebene Funktion die kanonische SOP-Form

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = ∑ ( m1, m2, m3, m5 )

Die restlichen Terme dieser Funktion sind Maxterme, für die die Ausgabe falsch ist. Diese Max-Terme sind M0,M4,M6,M7. Diese Max-Terme werden im POS-Ausdruck als das Produkt dieser Max-Terme verwendet. Das Symbol für das Produkt ist ∏.

F = ∏ ( M0, M4, M6, M7)

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

Die Max-Terme sind das Komplement der Minterme. Deshalb ist M0=(A+B+C).

• Sie können auch lesen: Ripple Carry und Carry Look Ahead Adder

Umwandlung von kanonischer SOP in minimale SOP

Kanonische SOP kann in minimale SOP umgewandelt werden. Sie kann mit Hilfe der Karnaugh-Map oder der Booleschen algebraischen Theoreme umgewandelt werden. Die K-Map-Methode ist sehr einfach und ihr Beispiel wurde oben in der minimalen SOP-Form durchgeführt.

Summenprodukt

Summenprodukt abgekürzt für POS.

Die Summenproduktform ist eine Form, in der Produkte verschiedener Summenterme von Eingaben genommen werden. Es handelt sich dabei nicht um das arithmetische Produkt und die Summe, sondern um das logische boolesche UND bzw. ODER.

Um das Summenprodukt besser zu verstehen, müssen wir über den Maxterm Bescheid wissen.

Maxterm

Maxterm ist der Term oder Ausdruck, der für eine maximale Anzahl von Eingangskombinationen wahr oder für nur eine Kombination von Eingängen falsch ist.

Da das ODER-Gatter auch für nur eine Eingangskombination falsch ergibt. Maxterm ist also ODER von entweder komplementären oder nicht-komplementären Eingängen.

Die Maxterme für 3 Eingangsvariablen sind unten angegeben.

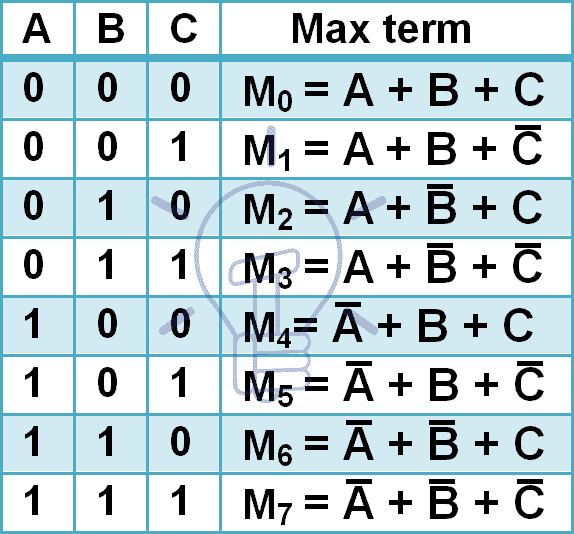
3 Eingänge haben 8 verschiedene Kombinationen, also hat es 8 Maxterme. Maxterme werden durch ein großes M und eine dezimale Kombinationsnummer im Index bezeichnet, wie in der obigen Tabelle gezeigt.

In Maxtermen wird jede Eingabe ergänzt, weil Maxterm nur dann ‚0‘ ergibt, wenn die genannte Kombination angewendet wird und Maxterm das Komplement von Minterm ist.

M3 = m̅3

M3 = (A̅BC)‘

M3 = A + B̅ +C̅ DE Morgans Gesetz

Deshalb besteht für A=0 Maxterm aus A & für A=1 Maxterm aus A̅.

Sie können auch lesen: Digitale Flip-Flops – SR, D, JK und T Flip-Flops

Arten von Summenproduktformen

Es gibt verschiedene Arten von Summenproduktformen.

• Kanonische POS-Form
• Nicht-kanonische Form
• Minimale POS-Form

Kanonische POS-Form

Sie ist auch bekannt als Produkt des Max-Terms oder Kanonische konjunktive Normalform (CCNF). Kanonisch bedeutet Normalform und konjunktiv bedeutet Schnittmenge.

In dieser Form werden Maxterme UND-verknüpft, für die die Ausgabe falsch ist.

Der kanonische POS-Ausdruck wird durch ∏ und Maxterme, für die die Ausgabe falsch ist, in Klammern dargestellt, wie im folgenden Beispiel gezeigt.

F = ∏ (M0, M4, M6, M7)

Erweiterung des Produkts

F = M0.M4.M6.M7

Max-Terme setzen

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

Die kanonische Form enthält in jedem Summenterm alle Eingänge entweder komplementiert oder nicht komplementiert.

• Sie können auch lesen: Clap Switch Circuit Electronic Project Using 555 Timer

Non – Canonical Form

Das Produkt eines Summenausdrucks, der nicht in der Standardform vorliegt, wird als nicht-kanonische Form bezeichnet.

Lassen Sie uns die oben angegebene Funktion als Beispiel nehmen.

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

F = (B+C) (A̅+B̅+C)(A̅+B̅+C̅)

Gleiche, aber invertierte Terme werden aus zwei Max-Termen eliminiert und bilden einen einzigen Term, um dies zu beweisen, hier ein Beispiel.

= (A+B+C) (A̅+B+C)

= AA̅+AB+AC+A̅B+BB+BC+A̅C+BC+CC

= 0+AB+AC+A̅B+A̅C+B+BC+C

= A(B+C)+A̅(B+C)+B(1+C)+C

= (B+C)(A+A̅)+B(1)+C

= (B+C)(0)+B+C

= B+C

Der erreichte Ausdruck ist immer noch in der Form des Summenprodukts, aber er ist nichtkanonische Form.

Minimale POS-Form

Dies ist die am meisten vereinfachte und optimierte Form eines POS-Ausdrucks, die nicht kanonisch ist. Die Form des minimalen Summenprodukts kann mit Hilfe boolescher algebraischer Theoreme erreicht werden, wie in dem oben genannten nicht-kanonischen Beispiel. Eine andere Methode zur Erreichung der minimalen POS-Form ist die Verwendung der Karnaugh-Map, die vergleichsweise einfacher ist als die Verwendung boolescher algebraischer Theoreme.

Die minimale POS-Form benötigt bei ihrer Implementierung weniger Eingänge und logische Gatter, weshalb sie wegen ihrer kompakten, schnellen und kostengünstigen Implementierung gegenüber der kanonischen Form bevorzugt wird.

Nehmen wir die obige Funktion als Beispiel

K-Map der Funktion

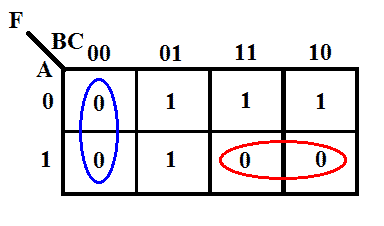
Minimaler Ausdruck mit K-Map

F = (B+C) (A̅+B̅)

Der erreichte Ausdruck ist das minimale Produkt der Summenform. Es ist immer noch ein Summenprodukt-Ausdruck, aber er benötigt nur 2 Eingänge, zwei ODER-Gatter und ein einziges UND-Gatter mit 2 Eingängen. Die kanonische Form benötigt jedoch 4 ODER-Gatter mit 3 Eingängen und 1 UND-Gatter mit 4 Eingängen.

• Sie können auch lesen: Negative Rückkopplung und negativ rückgekoppelte Verstärkersysteme

Schematischer Aufbau des Summenprodukts (POS)

Der Ausdruck Summenprodukt hat einen spezifischen schematischen Aufbau von ODER-UND. Bei der ODER-UND-Verknüpfung durchlaufen die Eingänge eine Reihe von ODER-Gattern, die die erste Ebene der Gatter darstellen, und die Ausgänge der ODER-Gatter der ersten Ebene durchlaufen die zweite Ebene des Gatters, das ein UND-Gatter ist.

Die Anzahl der Eingänge und der Gatter, die in diesem Entwurf verwendet werden, hängt von dem Ausdruck ab, der implementiert werden soll.

Die kanonische Form besteht aus der größtmöglichen Anzahl von Eingängen und Gattern, die minimale Form besteht jedoch aus der geringstmöglichen Anzahl von Eingängen und Gattern. Der schematische Aufbau der kanonischen und minimalen POS-Form ist unten angegeben.

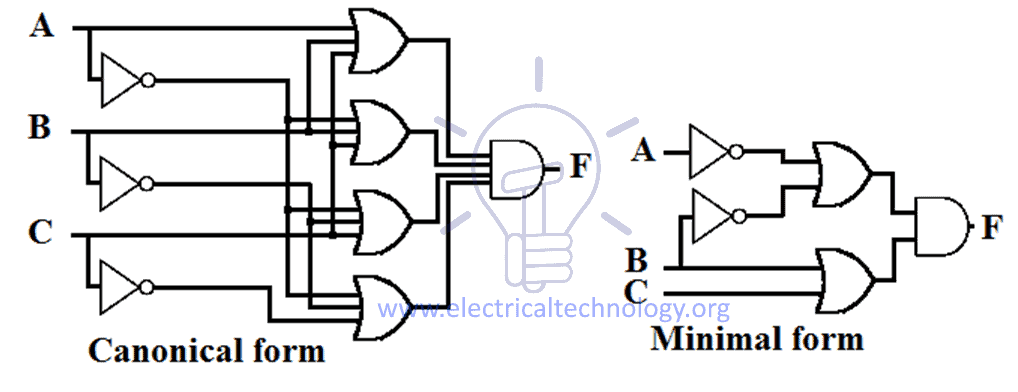
Umwandlung von der minimalen POS- in die kanonische POS-Form

Wie wir wissen, hat die kanonische Form von POS maximale Terme, und die maximalen Terme enthalten jeden Eingang, entweder komplementiert oder nicht komplementiert. Wir werden also jeden Summenterm mit dem Produkt aus komplementären und nicht-komplementären fehlenden Eingaben addieren.

Minimalform von POS

F = (A̅+B̅) (B+C)

(A̅+B̅) ist ein Begriff, dem die Eingabe C fehlt, so dass wir ihn mit (CC̅) ergänzen. Dem Begriff (B+C) fehlt die Eingabe von A, daher wird er um (AA̅) ergänzt.

F = (A̅+B̅+CC̅) (B+C+AA̅)

F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)(A̅+B+C)

Dieser Ausdruck hat jetzt die kanonische Form.

• Sie können auch lesen: Zähler und Arten von elektronischen Zählern

Umwandlung von kanonischer POS in SOP

Das Produkt des Summenausdrucks kann nur in die Summenform umgewandelt werden, wenn der Ausdruck in kanonischer Form ist. Kanonische POS und kanonische SOP sind interkonvertierbar, d.h. sie können ineinander umgewandelt werden. Ein Beispiel für die Umwandlung von POS in SOP ist unten angegeben.

POS kanonische Form

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

In der kanonischen Form ist jeder Summenterm ein Maximalterm, so dass er auch geschrieben werden kann als:

F = ∏(M0,M4,M6,M7)

Die verbleibenden Kombinationen von Eingängen sind Minterme der Funktion, für die ihr Ausgang wahr ist. Um sie in einen SOP-Ausdruck umzuwandeln, ändern wir zunächst das Symbol in Summation (∑) und verwenden das verbleibende Minterm.

F = ∑ (m1,m2,m3,m5)

Nun erweitern wir das Summationszeichen, um einen kanonischen SOP-Ausdruck zu bilden.

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

Min-Terme sind Komplemente von Max-Termen für die gleiche Kombination von Eingängen.

Kanonisch zu Minimal-POS

Ein kanonisches Summenprodukt kann mit Hilfe einer Karnaugh-Map (K-Map) in ein Minimalprodukt umgewandelt werden. Eine andere Methode zur Umwandlung von kanonischen in minimale Ausdrücke ist die Verwendung boolescher algebraischer Theoreme.

Die Verwendung von K-map ist sehr einfach, weshalb K-map bevorzugt wird. Für den minimalen POS-Ausdruck werden die 0’s in K-map zu Gruppen zusammengefasst und der Ausdruck, den wir erhalten, ist komplementär, da die Gruppen aus ‚0’s gemacht wurden. Das Beispiel wurde oben gemacht.

Lesen Sie auch:

• Digitales Logik-NICHT-Gatter – Digitales Inverter-Logik-Gatter
• Exklusiv-NOR (XNOR) Digitales Logik-Gatter
• Digitales Logik-NOR-Gatter
• Digitales Logik-NAND-Gatter