Funktionen oder Mapping

Nun werden wir uns in Funktionen oder Mapping mit einer besonderen Art von Beziehungen beschäftigen, die wir Funktionen oder Mapping nennen. Um sie zu verstehen, nehmen wir einige Beispiele aus dem wirklichen Leben.

Alle diese Fragen haben
eindeutige Antworten. Lassen Sie uns
sehen, wie wir
das in der Lernkartierung in Beziehung setzen können.

● Wo geht die Sonne auf?

Im Osten

● Welches ist die Hauptstadt von Indien?

Delhi

● Was ist der Nachfolger von 4?

5

● Was ist die Summe von 5 und 3?

8

Abbildung oder Funktionen:

Wenn A und B zwei nicht leere Mengen sind, dann sagt man, dass eine Beziehung ‚f‘ von der Menge A zur Menge B eine Funktion oder Abbildung ist,
● wenn jedes Element der Menge A mit einem einzigen Element der Menge B verbunden ist.

● Die Funktion ‚f‘ von A nach B wird durch f : A → B bezeichnet.

● Wenn f eine Funktion von A nach B ist und x ∈ A, dann ist f(x) ∈ B, wobei f(x) das Bild von x unter f und x das Vorbild von f(x) unter ‚f‘ genannt wird.

Anmerkung:

Damit f eine Abbildung von A nach B ist:

● Jedes Element von A muss ein Bild in B haben. Nebenstehende Abbildung stellt keine Abbildung dar, da das Element d in Menge A mit keinem Element der Menge B assoziiert ist.

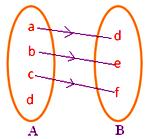
● Kein Element von A darf mehr als ein Bild haben. Nebenstehende Abbildung stellt keine Abbildung dar, da das Element b in der Menge A mit zwei Elementen d, f der Menge B assoziiert ist.

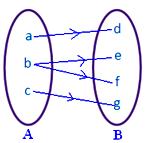
● Verschiedene Elemente von A können das gleiche Bild in B haben. Nebenstehende Abbildung stellt eine Abbildung dar.

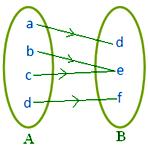
Hinweis:

Jede Abbildung ist eine Relation, aber nicht jede Relation ist eine Abbildung.

Funktion als eine besondere Art von Relation:

Erinnern wir uns an die Funktion als eine besondere Art von Relation: Angenommen, A und B sind zwei nicht leere Mengen, dann wird eine Regel ‚f‘, die jedes Element von A mit einem einzigen Element von B verbindet, eine Funktion oder eine Abbildung von A nach B genannt.
Wenn ‚f‘ eine Abbildung von A nach B ist,

dann drücken wir es aus als f: A → B

wir lesen es als ‚f‘ ist eine Funktion von A nach B.
Wenn ‚f‘ eine Funktion von A nach B ist und x∈A und y∈B, dann sagen wir, dass y das Bild des Elements x unter der Funktion ‚ f ‚ ist und bezeichnen es mit f(x).
Daher schreiben wir es als y = f(x)

Hier wird das Element x das Vorbild von y genannt.

Für eine Funktion von A nach B.
● A und B sollten nicht leer sein.

● Jedes Element von A soll ein Bild in B haben.

● Kein Element von ‚A‘ soll mehr als ein Bild in ‚B‘ haben.
Anmerkung:

● Zwei oder mehr Elemente von A können dasselbe Bild in B haben.

● f : x → y bedeutet, dass unter der Funktion ‚f‘ von A nach B ein Element x von A ein Bild y in B hat.

● Es ist notwendig, dass jedes Bild von f in B ist, aber es kann einige Elemente in B geben, die keine f-Bilder von irgendeinem Element von A sind.

● Relationen und Abbildungen

Geordnetes Paar

Kartesisches Produkt zweier Mengen

Relation

Domain und Range einer Relation

Funktionen oder Abbildungen

Domain Co-Domäne und Bereich einer Funktion

● Beziehungen und Mapping – Arbeitsblätter

Arbeitsblatt zu mathematischen Relationen

Arbeitsblatt zu Funktionen oder Abbildungen

Matheaufgaben für die 7. Klasse

Matheübungen für die 8. Klasse
Von den Funktionen oder der Zuordnung zur HOME PAGE