Forschungsmethoden in der Psychologie

Was ist Korrelationsforschung?

Korrelationsforschung ist eine Art der nicht-experimentellen Forschung, bei der der Forscher zwei Variablen (binär oder kontinuierlich) misst und die statistische Beziehung (d.h., (d. h. die Korrelation) zwischen ihnen mit geringen oder gar keinen Anstrengungen zur Kontrolle von Fremdvariablen. Es gibt viele Gründe, warum Forscher, die an statistischen Beziehungen zwischen Variablen interessiert sind, sich für eine Korrelationsstudie und nicht für ein Experiment entscheiden. Der erste Grund ist, dass sie nicht glauben, dass die statistische Beziehung eine kausale Beziehung ist, oder dass sie nicht an kausalen Beziehungen interessiert sind. Erinnern wir uns an die beiden Ziele der Wissenschaft: Beschreiben und Vorhersagen, und die Strategie der Korrelationsforschung ermöglicht es den Forschern, beide Ziele zu erreichen. Insbesondere kann diese Strategie verwendet werden, um die Stärke und Richtung der Beziehung zwischen zwei Variablen zu beschreiben, und wenn es eine Beziehung zwischen den Variablen gibt, dann können die Forscher die Ergebnisse einer Variablen verwenden, um die Ergebnisse der anderen vorherzusagen (unter Verwendung einer statistischen Technik namens Regression, die im Abschnitt über komplexe Korrelation in diesem Kapitel näher erläutert wird).

Ein weiterer Grund, warum Forscher eine Korrelationsstudie einem Experiment vorziehen, ist, dass die statistische Beziehung, die von Interesse ist, als kausal angesehen wird, der Forscher aber die unabhängige Variable nicht manipulieren kann, weil dies unmöglich, unpraktisch oder unethisch ist. Ein Forscher könnte sich zum Beispiel für den Zusammenhang zwischen der Häufigkeit des Cannabiskonsums und der Gedächtnisleistung interessieren, kann aber aus ethischen Gründen die Häufigkeit des Cannabiskonsums nicht beeinflussen. Daher müssen sie sich auf die Strategie der Korrelationsforschung verlassen; sie müssen einfach die Häufigkeit des Cannabiskonsums messen und ihre Gedächtnisfähigkeiten mit einem standardisierten Gedächtnistest messen und dann feststellen, ob die Häufigkeit des Cannabiskonsums in statistischem Zusammenhang mit der Gedächtnistestleistung steht.

Korrelation wird auch verwendet, um die Zuverlässigkeit und Gültigkeit von Messungen festzustellen. Zum Beispiel könnte ein Forscher die Gültigkeit eines kurzen Extraversionstests bewerten, indem er ihn einer großen Gruppe von Teilnehmern zusammen mit einem längeren Extraversionstest verabreicht, der sich bereits als gültig erwiesen hat. Der Forscher könnte dann überprüfen, ob die Ergebnisse des Kurztests stark mit den Ergebnissen des längeren Tests korreliert sind. Es wird davon ausgegangen, dass keiner der beiden Testwerte den anderen verursacht, so dass es keine unabhängige Variable gibt, die manipuliert werden muss. Die Begriffe „unabhängige Variable“ und „abhängige Variable“ treffen auf diese Art von Forschung nicht zu.

Eine weitere Stärke der Korrelationsforschung ist, dass sie oft eine höhere externe Validität aufweist als experimentelle Forschung. Es sei daran erinnert, dass es in der Regel einen Kompromiss zwischen interner Validität und externer Validität gibt. Je mehr Kontrollen zu den Experimenten hinzugefügt werden, desto größer ist die interne Validität, aber oft auf Kosten der externen Validität, da künstliche Bedingungen eingeführt werden, die in der Realität nicht existieren. Im Gegensatz dazu haben Korrelationsstudien in der Regel eine geringe interne Validität, da nichts manipuliert oder kontrolliert wird, aber sie haben oft eine hohe externe Validität. Da nichts vom Experimentator manipuliert oder kontrolliert wird, ist es wahrscheinlicher, dass die Ergebnisse Beziehungen widerspiegeln, die in der realen Welt bestehen.

Ausgehend von diesem Kompromiss zwischen interner und externer Validität kann die Korrelationsforschung schließlich dazu beitragen, konvergierende Beweise für eine Theorie zu liefern. Wenn eine Theorie sowohl durch ein echtes Experiment mit hoher interner Validität als auch durch eine Korrelationsstudie mit hoher externer Validität gestützt wird, können die Forscher mehr Vertrauen in die Gültigkeit ihrer Theorie haben. Ein konkretes Beispiel: Korrelationsstudien, die einen Zusammenhang zwischen dem Konsum von Gewaltfernsehen und aggressivem Verhalten nachweisen, wurden durch experimentelle Studien ergänzt, die bestätigen, dass es sich um eine kausale Beziehung handelt (Bushman & Huesmann, 2001).

Geht es bei der Korrelationsforschung immer um quantitative Variablen?

Ein weit verbreiteter Irrtum unter angehenden Forschern ist, dass bei der Korrelationsforschung zwei quantitative Variablen verwendet werden müssen, wie z. B. die Ergebnisse von zwei Extraversionstests oder die Anzahl der täglichen Probleme und die Anzahl der Symptome, die Menschen erlebt haben. Das entscheidende Merkmal der Korrelationsforschung ist jedoch, dass die beiden Variablen gemessen werden – keine der beiden Variablen wird manipuliert – und dies gilt unabhängig davon, ob die Variablen quantitativ oder kategorial sind. Stellen Sie sich zum Beispiel vor, dass ein Forscher die Rosenberg-Selbstwert-Skala an 50 amerikanische und 50 japanische College-Studenten verteilt. Obwohl sich dies wie ein Experiment zwischen den Versuchspersonen anfühlt“, handelt es sich um eine Korrelationsstudie, da der Forscher die Nationalitäten der Studenten nicht manipuliert hat. Das Gleiche gilt für die Studie von Cacioppo und Petty, in der Hochschullehrer und Fabrikarbeiter in Bezug auf ihr Erkenntnisbedürfnis verglichen werden. Es handelt sich um eine Korrelationsstudie, da die Forscher die Berufe der Teilnehmer nicht manipuliert haben.

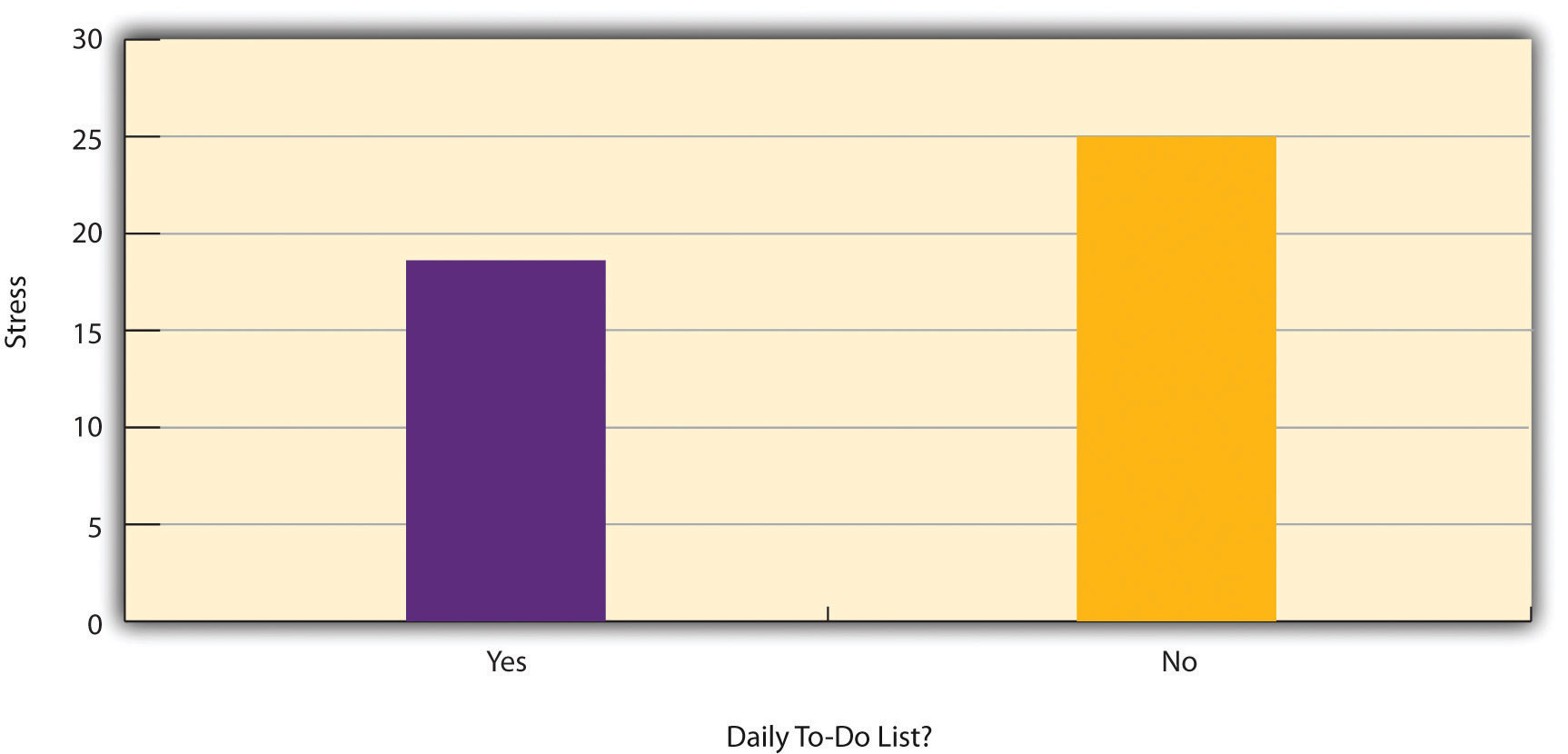
Abbildung 6.2 zeigt Daten aus einer hypothetischen Studie über den Zusammenhang zwischen der Tatsache, ob Menschen eine tägliche Liste von zu erledigenden Dingen (eine „To-Do-Liste“) erstellen, und Stress. Es ist unklar, ob es sich um ein Experiment oder eine Korrelationsstudie handelt, da nicht klar ist, ob die unabhängige Variable manipuliert wurde. Wenn der Forscher einige Teilnehmer nach dem Zufallsprinzip angewiesen hat, tägliche Aufgabenlisten zu erstellen, und andere nicht, dann handelt es sich um ein Experiment. Wenn der Forscher die Teilnehmer lediglich fragte, ob sie tägliche Aufgabenlisten erstellen, handelt es sich um eine Korrelationsstudie. Die Unterscheidung ist wichtig, denn wenn es sich bei der Studie um ein Experiment handelte, könnte man zu dem Schluss kommen, dass das Anfertigen der täglichen Aufgabenlisten den Stress der Teilnehmer verringert. Handelt es sich jedoch um eine Korrelationsstudie, könnte man nur zu dem Schluss kommen, dass diese Variablen statistisch gesehen zusammenhängen. Vielleicht wirkt sich Stress negativ auf die Fähigkeit der Menschen aus, vorausschauend zu planen (das Problem der Gerichtetheit). Oder vielleicht machen Menschen, die gewissenhafter sind, eher To-Do-Listen und sind weniger gestresst (das Problem der dritten Variable). Entscheidend ist, dass eine Studie nicht durch die untersuchten Variablen als experimentell oder korrelativ definiert wird, auch nicht dadurch, ob die Variablen quantitativ oder kategorisch sind, und auch nicht durch die Art des Diagramms oder der Statistik, die zur Analyse der Daten verwendet werden. Was eine Studie definiert, ist die Art und Weise, wie die Studie durchgeführt wird.

Datenerhebung in der Korrelationsforschung

Auch hier ist das definierende Merkmal der Korrelationsforschung, dass keine der Variablen manipuliert wird. Es spielt keine Rolle, wie oder wo die Variablen gemessen werden. Ein Forscher könnte Teilnehmer in ein Labor kommen lassen, um eine computergestützte Aufgabe zur rückwärts gerichteten Ziffernspanne und eine computergestützte Aufgabe zur risikoreichen Entscheidungsfindung zu bearbeiten und dann die Beziehung zwischen den Ergebnissen der Teilnehmer bei den beiden Aufgaben zu bewerten. Oder ein Forscher könnte in einem Einkaufszentrum Menschen zu ihrer Einstellung gegenüber der Umwelt und ihren Einkaufsgewohnheiten befragen und anschließend die Beziehung zwischen diesen beiden Variablen bewerten. Beide Studien wären korrelational, da keine unabhängige Variable manipuliert wird.

Korrelationen zwischen quantitativen Variablen

Korrelationen zwischen quantitativen Variablen werden oft durch Streudiagramme dargestellt. Abbildung 6.3 zeigt einige hypothetische Daten über die Beziehung zwischen dem Ausmaß des Stresses, dem Menschen ausgesetzt sind, und der Anzahl der körperlichen Symptome, die sie haben. Jeder Punkt im Streudiagramm stellt den Wert einer Person für beide Variablen dar. Der eingekreiste Punkt in Abbildung 6.3 steht zum Beispiel für eine Person, deren Stresswert 10 beträgt und die drei körperliche Symptome hat. Wenn man alle Punkte berücksichtigt, kann man sehen, dass Menschen, die mehr Stress haben, auch mehr körperliche Symptome haben. Dies ist ein gutes Beispiel für eine positive Beziehung, bei der höhere Werte für eine Variable tendenziell mit höheren Werten für die andere Variable verbunden sind. Mit anderen Worten, sie bewegen sich in dieselbe Richtung, entweder beide nach oben oder beide nach unten. Eine negative Beziehung ist eine Beziehung, bei der höhere Werte bei einer Variablen tendenziell mit niedrigeren Werten bei der anderen Variablen einhergehen. Mit anderen Worten, sie bewegen sich in entgegengesetzte Richtungen. Es besteht beispielsweise eine negative Beziehung zwischen Stress und der Funktion des Immunsystems, da höherer Stress mit einer geringeren Funktion des Immunsystems einhergeht.

Die Stärke einer Korrelation zwischen quantitativen Variablen wird in der Regel mit einer Statistik namens Pearson’s Korrelationskoeffizient (oder Pearson’s r) gemessen. Wie Abbildung 6.4 zeigt, reicht Pearson’s r von -1,00 (stärkstmögliche negative Beziehung) bis +1,00 (stärkstmögliche positive Beziehung). Ein Wert von 0 bedeutet, dass keine Beziehung zwischen den beiden Variablen besteht. Wenn Pearson’s r 0 ist, bilden die Punkte auf einem Streudiagramm eine formlose „Wolke“. Wenn sich der Wert in Richtung -1,00 oder +1,00 bewegt, nähern sich die Punkte immer mehr einer einzigen geraden Linie an. Korrelationskoeffizienten in der Nähe von ±.10 gelten als klein, Werte in der Nähe von ±.30 gelten als mittel und Werte in der Nähe von ±.50 als groß. Beachten Sie, dass das Vorzeichen von Pearson’s r nichts mit seiner Stärke zu tun hat. Pearson’s r-Werte von +,30 und -,30 sind beispielsweise gleich stark; der eine steht für eine mäßig positive Beziehung und der andere für eine mäßig negative Beziehung. Mit Ausnahme der Reliabilitätskoeffizienten sind die meisten Korrelationen, die wir in der Psychologie finden, klein oder mäßig groß. Die von Kristoffer Magnusson erstellte Website http://rpsychologist.com/d3/correlation/ bietet eine ausgezeichnete interaktive Visualisierung von Korrelationen, die es ermöglicht, die Stärke und Richtung einer Korrelation anzupassen und dabei die entsprechenden Veränderungen im Streudiagramm zu beobachten.

Es gibt zwei häufige Situationen, in denen der Wert von Pearson’s r irreführend sein kann. Pearson’s r ist nur für lineare Beziehungen, bei denen die Punkte am besten durch eine gerade Linie angenähert werden, ein gutes Maß. Es ist kein gutes Maß für nichtlineare Beziehungen, bei denen die Punkte besser durch eine gekrümmte Linie angenähert werden. Abbildung 6.5 zeigt beispielsweise eine hypothetische Beziehung zwischen der Menge an Schlaf, die Menschen pro Nacht bekommen, und dem Grad ihrer Depression. In diesem Beispiel ist die Linie, die sich den Punkten am besten annähert, eine Kurve – eine Art auf dem Kopf stehendes „U“ -, da Menschen, die etwa acht Stunden Schlaf bekommen, am wenigsten depressiv sind. Diejenigen, die zu wenig und die, die zu viel Schlaf bekommen, sind eher depressiv. Obwohl Abbildung 6.5 einen ziemlich starken Zusammenhang zwischen Depression und Schlaf zeigt, wäre Pearson’s r nahe Null, weil die Punkte im Streudiagramm nicht gut durch eine einzige gerade Linie passen. Das bedeutet, dass es wichtig ist, ein Streudiagramm zu erstellen und zu bestätigen, dass eine Beziehung annähernd linear ist, bevor man Pearson’s r verwendet. Nichtlineare Beziehungen sind in der Psychologie recht häufig, aber die Messung ihrer Stärke geht über den Rahmen dieses Buches hinaus.

Eine weitere häufige Situation, in der der Wert von Pearson’s r irreführend sein kann, ist, wenn eine oder beide Variablen in der Stichprobe im Vergleich zur Grundgesamtheit einen begrenzten Bereich aufweisen. Dieses Problem wird als Einschränkung des Bereichs bezeichnet. Nehmen wir zum Beispiel an, dass es eine starke negative Korrelation zwischen dem Alter der Personen und ihrer Vorliebe für Hip-Hop-Musik gibt, wie aus dem Streudiagramm in Abbildung 6.6 hervorgeht. Pearson’s r ist hier -.77. Würden wir jedoch nur Daten von 18- bis 24-Jährigen erheben – dargestellt durch den schraffierten Bereich in Abbildung 6.6 -, wäre die Beziehung offenbar recht schwach. Tatsächlich beträgt Pearson’s r für diesen eingeschränkten Altersbereich 0. Es ist daher eine gute Idee, Studien so zu konzipieren, dass eine Einschränkung des Bereichs vermieden wird. Wenn beispielsweise das Alter eine der Hauptvariablen ist, können Sie Daten von Personen aus einem breiten Altersspektrum erheben. Da eine Einschränkung der Spannweite jedoch nicht immer zu erwarten oder leicht zu vermeiden ist, empfiehlt es sich, die Daten auf eine mögliche Einschränkung der Spannweite hin zu untersuchen und Pearson’s r in diesem Zusammenhang zu interpretieren. (Es gibt auch statistische Methoden zur Korrektur von Pearson’s r bei eingeschränktem Bereich, die jedoch den Rahmen dieses Buches sprengen würden).

Korrelation impliziert keine Kausalität

Sie haben wahrscheinlich schon oft gehört, dass „Korrelation keine Kausalität impliziert“. Ein amüsantes Beispiel dafür stammt aus einer Studie aus dem Jahr 2012, die eine positive Korrelation (Pearson’s r = 0,79) zwischen dem Pro-Kopf-Schokoladenkonsum einer Nation und der Anzahl der Nobelpreise, die den Bürgern dieser Nation verliehen wurden, zeigte. Es scheint jedoch klar zu sein, dass dies nicht bedeutet, dass der Verzehr von Schokolade dazu führt, dass Menschen Nobelpreise gewinnen, und es wäre nicht sinnvoll, zu versuchen, die Zahl der gewonnenen Nobelpreise zu erhöhen, indem man Eltern empfiehlt, ihren Kindern mehr Schokolade zu geben.

Es gibt zwei Gründe dafür, dass Korrelation keine Kausalität impliziert. Der erste Grund ist das sogenannte Direktionalitätsproblem. Zwei Variablen, X und Y, können statistisch zusammenhängen, weil X Y verursacht oder weil Y X verursacht. Nehmen wir zum Beispiel eine Studie, die zeigt, dass die Frage, ob Menschen Sport treiben oder nicht, statistisch damit zusammenhängt, wie glücklich sie sind – so dass Menschen, die Sport treiben, im Durchschnitt glücklicher sind als Menschen, die das nicht tun. Diese statistische Beziehung stimmt mit der Vorstellung überein, dass Sport Glück verursacht, aber sie stimmt auch mit der Vorstellung überein, dass Glück den Sport verursacht. Vielleicht gibt Glück den Menschen mehr Energie oder veranlasst sie dazu, Gelegenheiten zu suchen, mit anderen in Kontakt zu treten, indem sie ins Fitnessstudio gehen. Der zweite Grund dafür, dass Korrelation nicht gleichbedeutend mit Kausalität ist, wird als Problem der dritten Variable bezeichnet. Zwei Variablen, X und Y, können statistisch zusammenhängen, nicht weil X Y verursacht oder weil Y X verursacht, sondern weil eine dritte Variable, Z, sowohl X als auch Y verursacht. Die Tatsache, dass Nationen, die mehr Nobelpreise gewonnen haben, tendenziell einen höheren Schokoladenkonsum haben, spiegelt wahrscheinlich die Geografie wider, da europäische Länder tendenziell einen höheren Pro-Kopf-Schokoladenkonsum haben und mehr in Bildung und Technologie investieren (wiederum pro Kopf) als viele andere Länder der Welt. In ähnlicher Weise könnte der statistische Zusammenhang zwischen Bewegung und Glück bedeuten, dass eine dritte Variable, z. B. die körperliche Gesundheit, die beiden anderen bedingt. Körperliche Gesundheit könnte die Menschen dazu bringen, Sport zu treiben und glücklicher zu sein. Korrelationen, die auf eine dritte Variable zurückzuführen sind, werden oft als Scheinkorrelationen bezeichnet.

Ein paar ausgezeichnete und amüsante Beispiele für Scheinkorrelationen finden Sie unter http://www.tylervigen.com (Abbildung 6.7 zeigt ein solches Beispiel).