Datenstrukturen: Stapel und Warteschlangen – Designveloper

Warum Stapel und Warteschlangen?

Im Gegensatz zu einem Array gibt es bei Stapeln und Warteschlangen keine zufällige Zugriffsoperation (wir können nicht direkt mit einem ‚Index‘ auf ein Element zugreifen). Wir haben in der Regel weniger Methoden/Aktionen, auf die wir zugreifen können, wie z.B. push(), pop(), peek(), enqueue(), dequeue(), die sich alle ausschließlich mit dem Element am Anfang oder am Ende der Datenstruktur beschäftigen.

Aber…

Frage: Das klingt so einschränkend, da wir nur auf das erste oder das letzte Element in der Datenstruktur zugreifen können. Warum sollten wir so etwas überhaupt verwenden wollen? Warum verwenden wir nicht einfach Arrays für mehr Flexibilität?

Antwort: Stapel und Warteschlangen sind in der Regel „Datenstrukturen auf höherer Ebene“, die auf Datenstrukturen auf niedrigerer Ebene (Arrays oder verkettete Listen) aufgesetzt werden, um die Operationen einzuschränken, die wir mit ihnen durchführen können. Das ist ein Vorteil, wenn wir einen eingeschränkten Zugriff wünschen.

Diese eingeschränkte Fähigkeit einer Datenstruktur ist ein Vorteil, weil wir kontrollieren können, wer diese Datenstruktur verwendet, die nur richtige Operationen ausführt, die effizient sind. Wir müssen uns zum Beispiel nicht wundern, wenn jemand zufällig ein Element in die Mitte unserer Liste einfügt und damit einige Invarianten durcheinander bringt. Das hat uns vor einer Menge Probleme bewahrt. Schauen wir sie uns genauer an.

Was ist ein Stack?

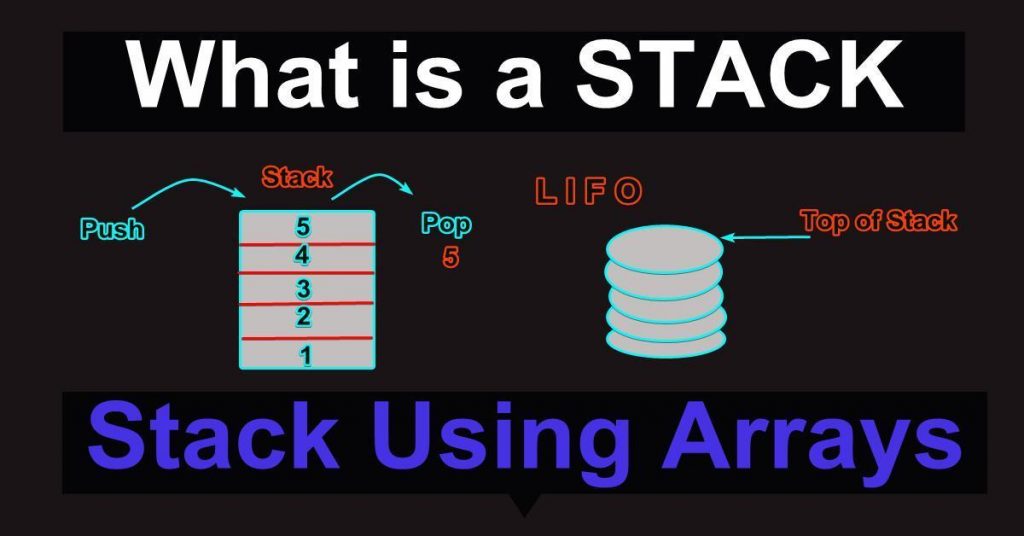
Ein Stack ist eine lineare Datenstruktur mit einem Ende, die einen realen Stack mit zwei primären Operationen modelliert, nämlich Push und Pop.

In diesem Bild unten können wir sehen, dass ein Datenelement vom oberen Ende des Stacks entfernt und ein anderes hinzugefügt wird. Es gibt einen oberen Zeiger, der auf den Block an der Spitze des Stacks zeigt. Der Grund dafür ist, dass Elemente in einem Stapel immer entfernt und an der Spitze des Stapels hinzugefügt werden. Dieses Verhalten ist allgemein als LIFO (Last In First Out) bekannt.

Stapeloperationen

Nachfolgend sind die 2 grundlegenden Operationen aufgeführt, die auf einem Stapel ausgeführt werden können.

• Push-Funktion: Hinzufügen eines Elements an die Spitze des Stapels
• Pop-Funktion: Entfernt das oberste Element (und gibt es ggf. zurück)

Visualisierung der grundlegenden Operationen eines Stapels

Darüber hinaus gibt es folgende zusätzliche Funktionen für einen Stapel, um seinen Status zu überprüfen.

• Peek-Funktion: Gibt das oberste Element des Stapels zurück, ohne es zu entfernen oder zu löschen
• Funktion isEmpty: Prüfen, ob der Stapel leer ist oder nicht
• isFull Funktion: Prüfen, ob der Stapel voll ist oder nicht

Alles arbeitet auf der Oberseite des Stapels. Wir haben nur Zugriff auf den obersten Teil. Das ist wichtig, um zu verstehen, wie er funktioniert.

Komplexitätsanalyse

Die folgende Komplexitätstabelle geht davon aus, dass Sie einen Stack mit einer verknüpften Liste implementiert haben

Stapelanwendungen

Wann und wo wird ein Stack verwendet? Wir verwenden Stack oft in der Programmierung, ohne es zu bemerken, hier sind einige Beispiele:

• Kann für die Auswertung von Ausdrücken verwendet werden (z.B.: ein Shunt-Algorithmus zum Parsen und Auswerten mathematischer Ausdrücke).
• Kann zur Implementierung von Funktionsaufrufen in der Rekursionsprogrammierung verwendet werden.

• Wird von Rückgängigmach-Mechanismen in Texteditoren verwendet, um geschriebenen Text rückgängig zu machen (Cmd + Z unter Mac OS und Ctrl + Z unter Windows)
• Wird im Browser verwendet, um vorwärts und rückwärts zu navigieren vorwärts zu navigieren
• Kann verwendet werden, um eine Tiefensuche (DFS) in einem Graphen durchzuführen
• Wird hinter den Kulissen verwendet, um Rekursion zu unterstützen, indem vorherige Funktionsaufrufe verfolgt werden

Was ist eine Warteschlange?

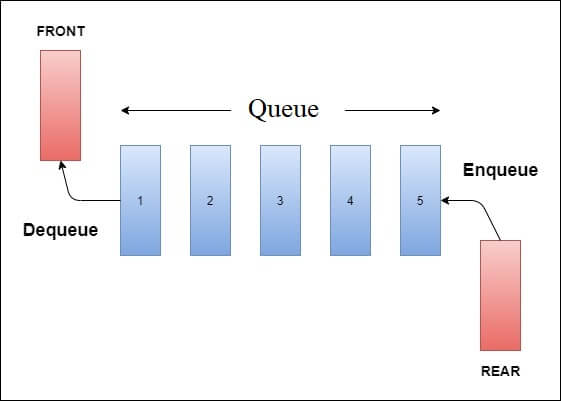
Eine Warteschlange ist ebenfalls eine lineare Datenstruktur, die reale Warteschlangen modelliert, indem sie zwei primäre Operationen hat, nämlich enqueue (wir können uns das als „in die Warteschlange eintreten“ vorstellen) und dequeue (wir können uns das auch als „aus der Warteschlange löschen“ vorstellen). Diese Struktur wird „Warteschlange“ genannt, weil sie einer realen Warteschlange ähnelt (wo Menschen in einer Schlange warten).

Jede Warteschlange hat ein vorderes und ein hinteres Ende (manchmal auch „hinten“ genannt). Wir fügen Elemente durch die Rückseite ein und entfernen sie durch die Vorderseite.

Eine Warteschlange ist eine FIFO-Struktur (First In First Out – das Element, das zuerst platziert wird, kann als erstes aufgerufen werden), die in vielen Programmiersprachen zu finden ist.

Warteschlangenoperationen

Im Folgenden sind die 3 grundlegenden Operationen aufgeführt, die mit einer Warteschlange durchgeführt werden können.

• Enqueue-Funktion: Hinzufügen eines Elements an das Ende der Warteschlange
• Dequeue-Funktion: Entfernen des Elements vom Anfang der Warteschlange
• Peeking-Funktion: Betrachtung des Wertes am Anfang der Warteschlange, ohne ihn zu entfernen

Komplexitätsanalyse

Wie in der Abbildung zu sehen ist, benötigen die Operationen Enqueuing und Dequeuing konstante Zeit O(1). Die Überprüfung, ob ein Element in der Warteschlange enthalten ist, benötigt jedoch lineare Zeit O(n), da wir potenziell alle Elemente durchsuchen müssten.

Es gibt auch ein internes Entfernen von Elementen (nicht aus der Warteschlange). Dies erfordert lineare Zeit, da wir im schlimmsten Fall alle Elemente durchsuchen müssen.

Warteschlangen-Anwendungen

• Verwendet, um Threads in Multithreading zu verwalten.
• Kann verwendet werden, um die x zuletzt hinzugefügten Elemente effizient zu verfolgen
• Web-Server-Anfrage-Management, wo wir zuerst kommen, um zu bedienen. Ein Beispiel: Zu einem bestimmten Zeitpunkt kann unser Webserver nur maximal 50 Personen gleichzeitig bedienen.

Wenn in einem kurzen Zeitraum 70 Anfragen eingehen, können wir nicht alle bearbeiten. Deshalb holt der Webserver nur 50 Anfragen aus der Warteschlange und legt die restlichen 20 in die Warteschleife. Wenn der Webserver mit der Bearbeitung einer Anfrage fertig ist, wird die nächste Anfrage aus der Warteschlange genommen, und zwar so lange, bis die Warteschlange leer ist.

• Breadth-first search (BFS) graph traversal
• Verwendet zur Implementierung von Warteschlangensystemen (z. B.: Prioritätswarteschlangen)
• Verwendet in Netzwerkdruckern: Der Drucker kann immer nur eine einzige Anfrage bedienen. Wenn also andere Anfragen kommen, während der Drucker beschäftigt ist, wird das Programm, das den Drucker verwaltet, diese Anfragen nicht abweisen, sondern sie in eine Warteschlange stellen, die auf die Ausführung wartet. Die erste Anfrage wird zuerst bedient (FIFO).

Wir hoffen, dass dieser Artikel Ihnen ein Bild von Stapeln und Warteschlangen vermittelt hat. Vergessen Sie nicht, unseren Blog zu abonnieren und Designveloper’s Facebook, Twitter und LinkedIn zu folgen.

Und dies sind andere Artikel, die Ihnen gefallen könnten:

• Was ist Web Application Architecture?
• Datenstrukturen und ihre Anwendungen
• Was ist die Big O Notation?