2.12: Van-der-Waals-Gleichung

Eine auf van der Waals zurückgehende Gleichung erweitert die ideale Gasgleichung auf einfache Weise. Die Van-der-Waals-Gleichung ist

Sie passt besser zu den Druck-Volumen-Temperatur-Daten eines realen Gases als die ideale Gasgleichung. Die verbesserte Anpassung wird durch die Einführung von zwei Parametern (bezeichnet als „\(a\)“ und „\(b\)“) erreicht, die für jedes Gas experimentell bestimmt werden müssen. Die Van-der-Waals-Gleichung ist besonders nützlich, um das Verhalten realer Gase zu verstehen, da sie ein einfaches physikalisches Bild für den Unterschied zwischen einem realen Gas und einem idealen Gas liefert.

Bei der Ableitung des Boyle’schen Gesetzes aus den Newton’schen Gesetzen wird angenommen, dass die Gasmoleküle nicht miteinander wechselwirken. Einfache Argumente zeigen, dass dies nur annähernd richtig sein kann. Echte Gasmoleküle müssen miteinander wechselwirken. Bei kurzen Abständen stoßen sie sich gegenseitig ab. Bei etwas größeren Abständen ziehen sie sich gegenseitig an. Die Gleichung des idealen Gases kann auch aus den grundlegenden Annahmen, die wir in § 10 gemacht haben, durch Anwendung der Theorie der statistischen Thermodynamik abgeleitet werden. Wenn wir verschiedene Annahmen über die Eigenschaften von Molekülen treffen, können wir die statistische Thermodynamik anwenden, um die van der Waals-Gleichung abzuleiten. Die erforderlichen Annahmen sind, dass die Moleküle ein endliches Volumen einnehmen und dass sie sich gegenseitig mit einer Kraft anziehen, die als Kehrwert einer Potenz des Abstands zwischen ihnen variiert. (Man nimmt gewöhnlich an, dass die Anziehungskraft proportional zu \(r^{-6}\) ist.)

Um zu erkennen, dass reale Gasmoleküle einander sowohl anziehen als auch abstoßen, müssen wir uns nur daran erinnern, dass jedes Gas verflüssigt werden kann, indem man seine Temperatur senkt und den auf es ausgeübten Druck erhöht. Wenn wir die Flüssigkeit weiter abkühlen, gefriert sie zu einem Feststoff. Ein Festkörper zeichnet sich dadurch aus, dass er seine Form beibehält und dass er nahezu inkompressibel ist. Wir führen die Inkompressibilität eines Festkörpers auf die Abstoßungskräfte zwischen den Molekülen zurück, die sich so sehr angenähert haben, dass die Abstoßungskräfte zwischen ihnen wichtig geworden sind. Um den Festkörper zu komprimieren, müssen die Moleküle noch enger zusammengeschoben werden, was eine übermäßige Kraft erfordert. Wenn wir dagegen einen Eiswürfel quer durch den Raum werfen, fliegen alle Wassermoleküle, aus denen er besteht, gemeinsam durch den Raum. Offensichtlich werden die Wassermoleküle in dem Festkörper voneinander angezogen, sonst würden sie alle ihren eigenen Weg gehen – das Werfen des Eiswürfels wäre wie das Werfen einer Handvoll trockenen Sandes. Aber Wassermoleküle sind unabhängig von der Temperatur oder dem Druck dieselben Moleküle. Wenn es also Anziehungs- und Abstoßungskräfte zwischen ihnen in der festen Phase gibt, müssen diese Kräfte auch in der flüssigen und gasförmigen Phase vorhanden sein.

In der Gasphase sind die Moleküle weit voneinander entfernt; in der flüssigen oder festen Phase sind sie dicht beieinander. Am Siedepunkt ist das Volumen einer Flüssigkeit viel kleiner als das Volumen des Gases, aus dem sie kondensiert ist. Am Gefrierpunkt unterscheidet sich das Volumen eines Festkörpers nur geringfügig vom Volumen der Flüssigkeit, aus der er gefroren ist, und es ist mit Sicherheit größer als Null. Diese alltäglichen Beobachtungen lassen sich leicht erklären, wenn man annimmt, dass jedes Molekül ein charakteristisches Volumen hat. Dies ist wiederum eine Folge der Natur der zwischenmolekularen Kräfte, die offensichtlich stärker werden, wenn der Abstand zwischen einem Molekülpaar abnimmt. Da eine Flüssigkeit oder ein Feststoff ein bestimmtes Volumen einnimmt, muss die abstoßende Kraft schneller zunehmen als die anziehende Kraft, wenn der zwischenmolekulare Abstand klein ist. Oft ist es sinnvoll, vom molaren Volumen einer kondensierten Phase zu sprechen. Unter molarem Volumen versteht man das Volumen von einem Mol einer reinen Substanz. Das molare Volumen einer kondensierten Phase wird durch den intermolekularen Abstand bestimmt, bei dem ein Gleichgewicht zwischen den intermolekularen Anziehungs- und Abstoßungskräften besteht.

In kondensierten Phasen liegen die Moleküle offensichtlich sehr nahe beieinander. Wenn man annimmt, dass die Leerräume zwischen den Molekülen vernachlässigbar sind, ist das Volumen einer kondensierten Phase ungefähr gleich der Anzahl der Moleküle in der Probe multipliziert mit dem Volumen eines einzelnen Moleküls. Das molare Volumen ist dann die Avogadrosche Zahl mal dem von einem Molekül eingenommenen Volumen. Wenn wir die Dichte, D, und die molare Masse, \(\overline{M}\), kennen, können wir das molare Volumen, \(\overline{V}\), wie folgt ermitteln

\

Das von einem Molekül eingenommene Volumen, V\({}_{Molekül}\), wird

\

Der Druck und das Volumen, die in der van der Waals-Gleichung erscheinen, sind der Druck und das Volumen des realen Gases. Wir können die Terme in der van der Waals’schen Gleichung mit der idealen Gasgleichung in Beziehung setzen: Es ist nützlich, sich die Terme \(\left(P+{{an}^2}/{V^2}\right)\) und \(\left(V-nb\right)\) als den Druck und das Volumen eines hypothetischen idealen Gases vorzustellen. Das heißt

\ &=nRT \end{align*}\]

Dann haben wir

\

Wir leiten die ideale Gasgleichung aus einem Modell ab, in dem die Moleküle nicht wechselwirkende Punktmassen sind. Das Volumen eines idealen Gases ist also das Volumen, das von einem Gas eingenommen wird, dessen einzelne Moleküle das Volumen Null haben. Wenn die einzelnen Moleküle eines realen Gases effektiv ein Volumen \({b}/{\overline{N}}\) einnehmen, dann nehmen \(n\) Mole von ihnen effektiv ein Volumen

\

Van der Waals‘ Gleichung besagt, dass das Volumen eines realen Gases das Volumen ist, das von nicht wechselwirkenden Punktmassen eingenommen würde, \(V_{ideal\ gas}}), plus das effektive Volumen der Gasmoleküle selbst. (Wenn Daten für reale Gasmoleküle an die van der Waals-Gleichung angepasst werden, ist der Wert von \(b\) in der Regel etwas größer als das aus der Flüssigkeitsdichte und dem Molekulargewicht geschätzte Volumen. Siehe Problem 24.)

In ähnlicher Weise haben wir

\

Wir können dies als eine logische Folge der anziehenden Wechselwirkungen zwischen den Molekülen des realen Gases verstehen. Mit \(a>0\) heißt es, dass der Druck des realen Gases um einen Betrag geringer ist als der Druck des hypothetischen idealen Gases, der proportional zu \({\left({n}/{V}\right)}^2\) ist. Die Proportionalitätskonstante ist \(a\). Da \({n}/{V}\) die molare Dichte (Mole pro Volumeneinheit) der Gasmoleküle ist, ist sie ein Maß für die Konzentration. Die Anzahl der Zusammenstöße zwischen Molekülen der gleichen Art ist proportional zum Quadrat ihrer Konzentration. (Auf diesen Punkt gehen wir in den Kapiteln 4 und 5 näher ein.) \({\left({n}/{V}\right)}^2\) ist also ein Maß für die Häufigkeit, mit der die realen Gasmoleküle in engen Kontakt miteinander kommen. Wenn sie sich gegenseitig anziehen, wenn sie einander nahe kommen, sollte die Wirkung dieser Anziehung proportional zu \({\left({n}/{V}\right)}^2\) sein. Die van-der-Waals-Gleichung stimmt also mit der Vorstellung überein, dass der Druck eines realen Gases sich vom Druck des hypothetischen idealen Gases um einen Betrag unterscheidet, der proportional zur Häufigkeit und Stärke der anziehenden Wechselwirkungen ist.

Aber warum sollten anziehende Wechselwirkungen diesen Effekt haben; warum sollte der Druck des realen Gases geringer sein als der des hypothetischen idealen Gases? Der beste Weg, sich ein qualitatives Bild zu machen, ist vielleicht die Erkenntnis, dass anziehende zwischenmolekulare Kräfte dazu führen, dass sich die Gasmoleküle verklumpen. Schließlich sind es diese Anziehungskräfte, die die Moleküle dazu bringen, bei niedrigen Temperaturen zu einer Flüssigkeit zu aggregieren. Oberhalb des Siedepunkts werden die Auswirkungen dieser Tendenz durch die Fähigkeit der Gasmoleküle, getrennte Wege zu gehen, begrenzt; aber auch im Gas müssen die Anziehungskräfte so wirken, dass das von den Molekülen eingenommene Volumen tendenziell verringert wird. Da das vom Gas eingenommene Volumen durch die Größe des Behälters und nicht durch die Eigenschaften des Gases selbst bestimmt wird, äußert sich diese Verklumpungstendenz in einer Abnahme des Drucks.

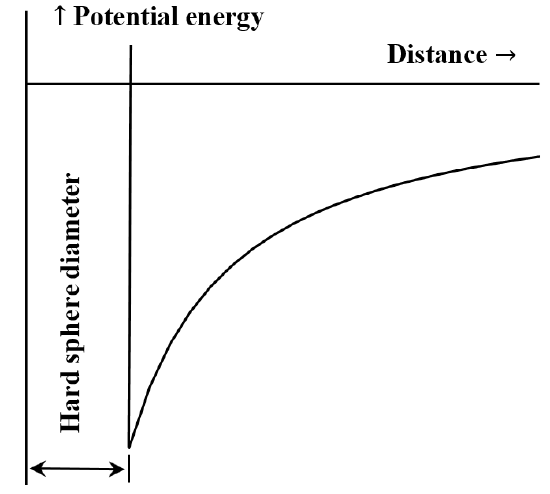
Es ist häufig nützlich, die Wechselwirkung zwischen Teilchen oder chemischen Einheiten in Form eines Diagramms der potentiellen Energie in Abhängigkeit vom Abstand zu beschreiben. Die van der Waals-Gleichung entspricht dem Fall, dass die abstoßende Wechselwirkung zwischen Molekülen nicht existiert, bis die Moleküle in Kontakt kommen. Sobald sie in Kontakt kommen, wird die Energie, die erforderlich ist, um sie noch näher zusammenzubringen, beliebig groß. Oft wird dies mit dem Ausdruck „harte Kugeln“ beschrieben. Die Anziehungskraft zwischen zwei Molekülen nimmt mit zunehmendem Abstand ab. Wenn sie sehr weit voneinander entfernt sind, ist die anziehende Wechselwirkung sehr gering. Wir sagen, dass die Energie der Wechselwirkung gleich Null ist, wenn die Moleküle unendlich weit voneinander entfernt sind. Sind zwei weit voneinander entfernte, stationäre Moleküle vorhanden, die sich gegenseitig anziehen, bewegen sie sich spontan aufeinander zu und gewinnen dabei an kinetischer Energie. Ihre potenzielle Energie nimmt mit zunehmender Annäherung ab und erreicht ihren kleinsten Wert, wenn die Moleküle in Kontakt kommen. Aus der van der Waals-Gleichung ergibt sich das in Abbildung 5 dargestellte Diagramm der potentiellen Energie in Abhängigkeit vom Abstand.