Sum Of Product (SOP) & Product Of Sum (POS)

Product Of Sum (POS) & Sum Of Product (SOP)

Sum Of Product (SOP)

Sum Of Product er den forkortede form af SOP. Sum of product form er en udtryksform i boolsk algebra, hvor forskellige produkttermer af indgange summeres sammen. Dette produkt er ikke aritmetisk multiplikation, men det er Boolsk logisk AND og Summen er Boolsk logisk OR.

For bedre at forstå SOP skal vi kende til min term.

Min Term

Minterm betyder den term, der er sand for et minimum antal kombinationer af input. Det er kun sandt for én kombination af indgange.

Da AND-gaten også kun giver Sandt, når alle dens indgange er sande, kan vi sige, at min-termer er AND af indgangskombinationer som i tabellen nedenfor.

3 indgange har 8 forskellige kombinationer. Hver kombination har en min-term, der betegnes med lille m, og dens decimale kombinationsnummer er skrevet i subscript. Hver af disse mintermer vil kun være sandt for den specifikke inputkombination.

• Du kan også læse: Digital Asynkron tæller (Ripple Counter) – Typer, Arbejde & Anvendelse

Typer af Sum Of Product (SOP) Former

Der er nogle få forskellige former for Sum Of Product (SOP).

• Kanonisk SOP-form
• Non-kanonisk SOP-form
• Minimal SOP-form

Kanonisk SOP-form

Dette er standardformen af Sum of Product. Den dannes ved at O Ring mintermerne af den funktion, for hvilken output er sandt. Dette er også kendt som Sum of Min-termer eller Canonical disjunctive normal form (CDNF). Det er blot et fancy navn. “Kanonisk” betyder “standardiseret” og “disjunktiv” betyder “Logisk OR union”.

Kanonisk SOP-udtryk er repræsenteret ved summationstegnet ∑ og mintermer i parenteserne, for hvilke output er sandt.

Til eksempel er en funktions sandhedstabel angivet nedenfor.

For denne funktion er det kanoniske SOP-udtryk

F = ∑( m1, m2, m3, m5 )

Hvilket betyder, at funktionen er sand for min-termerne {1, 2, 3, 5}.

Ved udvidelse af summeringen får vi.

F = m1 + m2 + m3 + m5

Nu sætter vi min-termerne ind i udtrykket

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

Kanonisk form indeholder alle indgange enten komplementeret eller ikke-komplementeret i sine produkttermer.

Du kan også læse: Du kan også læse: Digital synkron tæller – typer, arbejdsmetoder & Anvendelser

Ikke-kanonisk SOP-form

Som navnet antyder, er denne form den ikke-standardiserede form af SOP-udtryk. Produkttermerne er ikke min-termerne, men de er forenklet. Lad os tage ovenstående funktion i kanonisk form som et eksempel.

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = A̅B̅C + A̅B(C̅ + C) + AB̅C

F = A̅B̅C + A̅B(C̅ + C) + AB̅C

F = A̅B̅C + A̅B(1) + AB̅C

F = A̅B̅C + A̅B + AB̅C

Dette udtryk er stadig i summen af produktform, men det er ikkekanonisk eller ikke-standardiseret form.

Minimal SOP-form

Denne form er det mest forenklede SOP-udtryk for en funktion. Det er også en form af ikke-kanonisk form. Minimal SOP-form kan laves ved hjælp af Boolske algebraiske sætninger, men den er meget let at lave ved hjælp af Karnaugh-map (K-map).

Minimal SOP-form foretrækkes, fordi den bruger det mindste antal porte og indgangslinjer. den er kommercielt fordelagtig på grund af sin kompakte størrelse, hurtige hastighed og lave fremstillingsomkostninger.

Lad os tage et eksempel på den ovenfor angivne funktion i kanonisk form.

Dets K-map er angivet nedenfor.

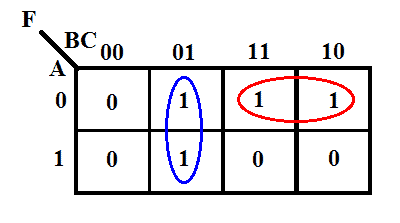
I henhold til K-map’et vil udgangsudtrykket være

F = B̅C + A̅B

Dette er det mest forenklede & optimerede udtryk for den nævnte funktion. Dette udtryk kræver kun to AND-gates med 2 indgange & en OR-gate med 2 indgange &. Den kanoniske form kræver dog fire 3-input AND-gates & fire 3-input AND-gates & en 4-input OR-gate, hvilket er relativt dyrere end implementeringen af den minimale form.

• Du kan også læse: Ring Counter & Johnson Counter – Konstruktion & Drift

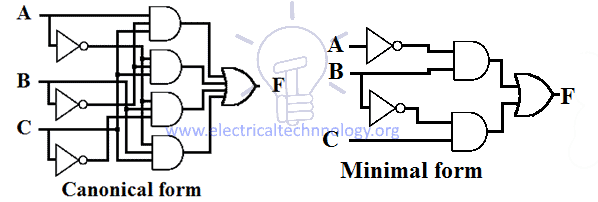
Skematisk design af Sum Of Product (SOP)

SOP-udtryk implementerer 2 niveau AND-OR design, hvor 1. niveau gate er AND gate efterfulgt af 2. niveau gate, som er OR gate. Skematisk design af SOP-udtryk kræver en gruppe array af AND-gates & en OR-gate.

Alle SOP-udtryk har nogenlunde samme design, dvs. alle indgange går gennem AND-gates, og derefter strømmer output fra disse AND-gates gennem en OR-gate, som vist i nedenstående figur.

Antal af indgange og antal AND-gates afhænger af det udtryk, man implementerer.

Eksempel på udformninger af kanoniske og minimale SOP-udtryk for en funktion er givet nedenfor.

Konvertering fra minimal SOP-form til kanonisk SOP-form

Konvertering fra minimal eller enhver form for ikke-kanonisk form til kanonisk form er meget enkel.

Som vi ved, har kanonisk form min termer & min termer består af alle indgange enten komplementeret eller ikke-komplementeret. Så vi vil multiplicere hver term i minimal SOP med summen af manglende input’s komplementerede og ikke-komplementerede form. Eksempel på konvertering for ovenstående funktion i minimal SOP-form er givet nedenfor.

Minimal SOP-form

F = A̅B + B̅C

Term A̅B mangler input C. Vi vil derfor gange A̅B med (C+C̅), fordi (C+C̅ = 1). Udtrykket B̅C mangler input A. så den vil blive ganget med (A+A̅)

F = A̅B(C + C̅) + B̅C(A + A̅)

F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C

Nu er dette udtryk i kanonisk form.

Konvertering fra kanonisk SOP til kanonisk POS

Standard SOP-udtryk kan konverteres til standard POS-udtryk (produkt af sum). F.eks. er den ovenfor angivne funktion i kanonisk SOP-form

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = ∑ ( m1, m2, m3, m5 )

De resterende termer i denne funktion er maxtermer, for hvilke output er falsk. Disse maxtermer er M0,M4,M6,M7. Disse max-termer vil blive anvendt i POS-udtrykket som produktet af disse max-termer. Symbolet for Produktet er ∏.

F = ∏ ( M0, M4, M6, M7)

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C)(A̅+B̅+C̅)

Max-termerne er komplementet til min-termerne. Hvilket er grunden til at M0=(A+B+C).

• Du kan også læse: Ripple Carry And Carry Look Ahead Adder

Konvertering fra kanonisk SOP til minimalt SOP

Kanonisk SOP kan konverteres til minimalt SOP. Det kan konverteres ved hjælp af Karnaugh map eller Boolean algebraiske sætninger. K-map-metoden er meget let, og dens eksempel er blevet udført ovenfor i den minimale SOP-form.

Sumprodukt

Sumprodukt forkortet for POS.

Sumproduktformen er en form, hvor produkter af forskellige sumtermermer af indgange tages. Disse er ikke aritmetiske produkt og sum, men de er henholdsvis logiske boolske AND og OR.

For bedre at forstå om Produkt af Sum, skal vi kende til Max term.

Max Term

Maxterm betyder den term eller det udtryk, der er sandt for et maksimalt antal inputkombinationer, eller som er falsk for kun én kombination af input.

Da OR gate også giver falsk for kun én inputkombination. Så maxterm er OR af enten komplementerede eller ikke-komplementerede input.

Maxtermer for 3 inputvariabler er givet nedenfor.

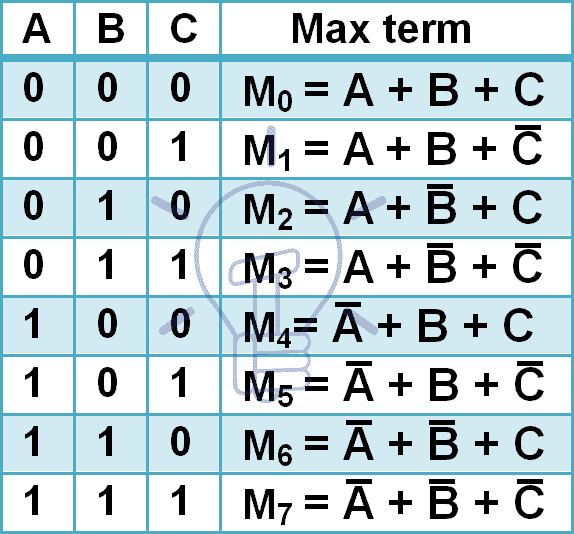
3 input har 8 forskellige kombinationer, så det vil have 8 maxtermer. Maxtermer betegnes med stort M og decimalt kombinationsnummer i subscriptet som vist i tabellen ovenfor.

I maxterm er hvert input komplementeret, fordi Maxterm kun giver “0”, når den nævnte kombination anvendes, og Maxterm er supplement til minterm.

M3 = m̅3

M3 = (A̅BC)’

M3 = A + B̅ +C̅ DE Morgans lov

Hvilket er grunden til at for A=0 Maxterm består A & for A=1 Maxterm består A̅.

Du kan også læse: Du kan også læse: Digitale Flip-Flops – SR-, D-, JK- og T-flipflops

Typer af produkt af sumformer

Der findes forskellige typer af produkt af sumformer.

• Canonical POS Form
• Non – Canonical Form
• Minimal POS Form

Canonical POS Form

Det er også kendt som Product of Max term eller Canonical conjunctive normal form (CCNF). Kanonisk betyder standard og konjunktiv betyder krydsning.

I denne form er Maxterms AND sammen, for hvilke output er falsk.

Kanonisk POS-udtryk er repræsenteret ved ∏ og Maxterms, for hvilke output er falsk, i parentes, som vist i eksemplet nedenfor.

F = ∏ (M0, M4, M6, M7)

Udvidelse af produktet

F = M0.M4.M6.M7

Sætte Max-termer

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

Den kanoniske form indeholder alle indgange enten komplementeret eller ikke-komplementeret i hver sin Sum-term.

• Du kan også læse: Lad os tage ovenstående funktion som et eksempel:

  Lad os tage den ovenfor givne funktion som et eksempel:

  Det produkt af sumudtryk, der ikke er i standardform, kaldes ikke-kanonisk form.

  F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

  F = (B+C) (A̅+B̅+C)(A̅+B̅+C)(A̅+B̅+C̅)

  Samme men omvendte udtryk eliminerer fra to Max udtryk og danner et enkelt udtryk for at bevise det her er et eksempel.

  = (A+B+C) (A̅+B+C)

  = AA̅+AB+AC+A̅B+BB+BC+A̅C+BC+CC

  = 0+AB+AC+A̅B+A̅C+B+B+BC+C

  = A(B+C)+A̅(B+C)+B(1+C)+C

  = A(B+C)+B(1+C)+C

  = (B+C)(A+A̅)+B(1)+C

  = (B+C)(0)+B+C

  = B+C

  Det opnåede udtryk er stadig i produkt af sumform, men det er ikkekanonisk form.

  Minimal POS-form

  Dette er den mest forenklede og optimerede form af et POS-udtryk, som ikke er kanonisk. Minimalt produkt af sumform kan opnås ved hjælp af Boolske algebraiske sætninger som i det ikke-kanoniske eksempel ovenfor. En anden metode til at opnå minimal POS-form er ved hjælp af Karnaugh-kort, som er forholdsvis lettere end at bruge Boolske algebraiske sætninger.

  Minimal POS-form bruger mindre antal indgange og logiske porte under gennemførelsen, og derfor foretrækkes de frem for den kanoniske form for deres kompakte, hurtige og billige gennemførelse.

  Lad os tage den ovenfor givne funktion som eksempel

  K-map af funktionen

  

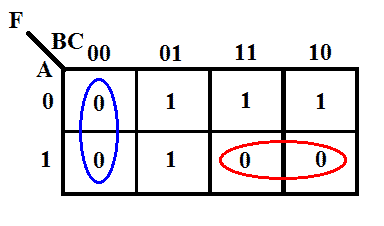
  Minimalt udtryk ved hjælp af K-map

  F = (B+C) (A̅+B̅)

  Det opnåede udtryk er det minimale produkt af sumform. Det er stadig produkt af sumudtryk Men det har kun brug for 2 indgange to OR-gates og en enkelt AND-gate med 2 indgange. Den kanoniske form har dog brug for 4 OR-gates med 3 indgange og 1 AND-gate med 4 indgange.

  • Du kan også læse: Negativ tilbagekobling og negativt tilbagekoblede forstærkersystemer

  Skematisk design af produkt af summen (POS)

  Udtrykket produkt af summen har et specifikt skematisk design af OR-AND. I OR-AND går indgangene gennem et array af OR-gates, som er første niveau af gates, og output fra OR-gates på første niveau går gennem andet niveau af gaten, som er en AND-gate.

  Antal af indgange og antal gates, der anvendes i dette design, afhænger af det udtryk, der skal implementeres.

  Den kanoniske form består af det maksimale antal mulige indgange og gates, men den minimale form består af det lavest mulige antal indgange og gates. Den skematiske udformning af den kanoniske og minimale POS-form er angivet nedenfor.

  

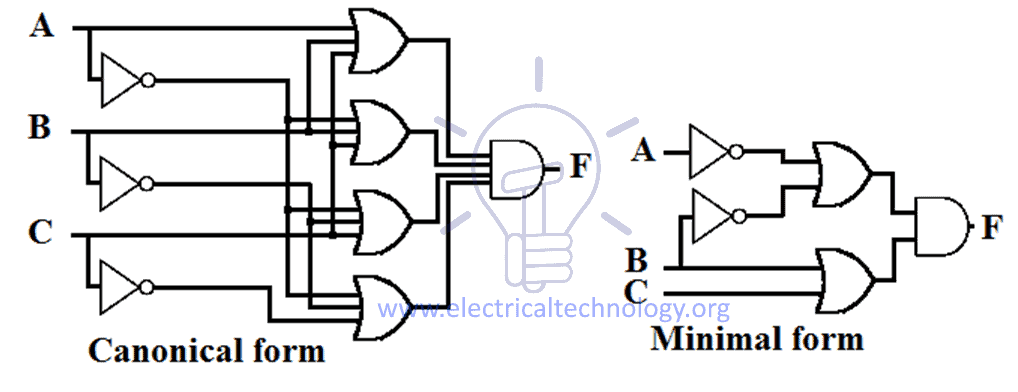
  Konvertering fra minimal POS til kanonisk form POS

  Som vi ved, har den kanoniske form af POS maks. termer, og maks. termer indeholder hvert input enten komplementeret eller ikke-komplementeret. Så vi vil tilføje hver sumtermin med produktet af komplementerede og ikke-komplementerede manglende input. Eksempel på omdannelsen er givet nedenfor.

  Minimal POS-form

  F = (A̅+B̅) (B+C)

  (A̅+B̅) er manglende C input, så vi vil tilføje (CC̅) med det. (B+C)-udtrykket mangler A-input, så vi tilføjer (AA̅) med det.

  F = (A̅+B̅+CC̅) (B+C+AA̅)

  F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)(A̅+B+C)(A̅+B+C)

  Dette udtryk er nu i kanonisk form.

  • Du kan også læse: Du kan også læse mere om: Tæller og typer af elektroniske tællere

  Konvertering fra kanonisk POS til SOP

  Udtrykket produkt af summen kan kun konverteres til summen af produktformen, hvis udtrykket er i kanonisk form. Kanonisk POS og kanonisk SOP er indbyrdes konverterbare, dvs. de kan konverteres til hinanden. Et eksempel på konvertering af POS til SOP er givet nedenfor.

  POS kanonisk form

  F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)(A̅+B̅+C̅)

  I kanonisk form er hvert summeterm et max-term, så det kan også skrives som:

  F = ∏(M0,M4,M6,M7)

  De resterende kombinationer af input er mintermer af den funktion, for hvilke dens output er sandt. For at konvertere det til SOP-udtryk ændrer vi først symbolet til summation (∑) og bruger de resterende mintermer.

  F = ∑ (m1,m2,m3,m5)

  Nu skal vi udvide summationstegnet til at danne et kanonisk SOP-udtryk.

  F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

  Min-termer er komplement til Max-termer for den samme kombination af input.

  Kanonisk til minimalt POS

  Et kanonisk produkt af sumudtryk kan omdannes til et minimalt produkt af sumform ved hjælp af Karnaugh map (K-map). En anden metode til at konvertere kanonisk til minimal er ved hjælp af Boolske algebraiske sætninger.

  Anvendelsen af K-map er meget let, hvorfor K-map foretrækkes. For minimalt POS-udtryk kombineres 0’erne i K-map i grupper, og det udtryk, vi får, er komplementeret, da grupperne blev lavet af ‘0’er. Dens eksempel er blevet udført ovenfor.

  Du kan også læse:

  • Digital Logic NOT Gate – Digital Inverter Logic Gate
  • Exclusive-NOR (XNOR) Digital Logic Gate
  • Digital Logic NOR Gate
  • Digital Logic NAND Gate
  • Digital Logic NAND Gate