Indkomstfordeling

Definition og måling af indkomstfordeling

Indkomstfordeling er den jævnhed eller lighed, hvormed indkomsten fordeles mellem medlemmerne af et samfund. Hvis alle tjener nøjagtig det samme beløb, er indkomstfordelingen fuldstændig lige. Hvis ingen tjener nogen penge undtagen én person, som tjener alle pengene, er indkomstfordelingen fuldstændig ulige. Normalt ligger indkomstfordelingen i et samfund dog et sted midt imellem lige og ulige indkomstfordeling.

Hvordan kan vi måle denne grad af lighed eller ulighed? Økonomer måler ofte indkomstlighed ved at måle, hvor meget indkomst de forskellige befolkningsgrupper tjener. Hvis vi f.eks. opdeler alle arbejdstagere i fem segmenter med hensyn til, hvor mange penge de tjener: de øverste 20 %, de anden 20 %, de tredje 20 %, de fjerde 20 % og de nederste 20 %, og vi får data om, hvor mange penge de tjener, kan vi derefter udarbejde et diagram, der viser, hvor meget indkomst hvert segment tjener ud af den samlede indkomst for alle arbejdstagere. Jo større forskellen er mellem de forskellige segmenter, jo større er indkomstuligheden.

Lad os sige, at gennemsnitsindkomsterne for fem segmenter i et samfund er 10.000 $, 24.000 $, 50.000 $, 80.000 $ og 110.000 $. For at se på indkomstfordelingen er vi nødt til at se, hvor stor en procentdel af den samlede indkomst hvert segment tjener, snarere end det faktiske beløb, som hvert segment tjener. Da hvert af segmenterne er lige store, behøver vi ikke at bekymre os om at vægte de gennemsnitlige indkomster, og vi kan foretage en simpel beregning af de enkelte segmenters indtjening som en del af det samlede beløb.

For den samlede indkomst bruger vi summen af de fem gennemsnitsindkomster:

Totalindkomst = 10000 + 24000 + 50000 + 80000 + 110000
Totalindkomst = 274000

Næst finder vi den procentdel af den samlede indkomst, som hvert segment af befolkningen tjener, ved at dividere deres indkomst med den samlede indkomst:

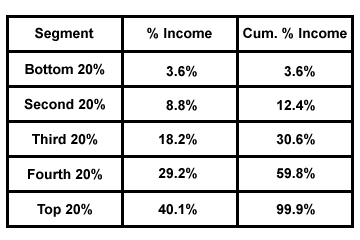
Segmentets nederste procentdel = 10000/274000 = 0.036 = 3,6 %
Sidste segment procentdel = 24000/274000 = 0,088 = 8.8%
Tredje segmentprocent = 50000/274000 = 0,182 = 18,2%
Fjerde segmentprocent = 80000/274000 = 0,292 = 29,2%
Top segmentprocent = 110000/274000 = 0,401 = 40,1%

Disse tal viser, at den nederste femtedel af befolkningen får mindre end 4% af den samlede indkomst, mens den øverste femtedel af befolkningen får over 40% af den samlede indkomst, hvilket indikerer en stor grad af indkomstulighed.

Økonomer ser også på kumulative tal for indkomstfordelingen. For at gøre dette skal man blot lægge procenterne sammen på hvert niveau, hvilket giver den indkomst, som alle personer på eller under et bestemt niveau har tjent. I vores eksempel ville det fungere på følgende måde:

Den kumulative procentdel i det nederste segment = 3,6 %
Den kumulative procentdel i det andet segment = 3,6 % + 8,8 % = 12,4 %
Den kumulative procentdel i det tredje segment = 12,4 % + 18,2 % = 30,6 %
Den kumulative procentdel i det fjerde segment = 30.6% + 29,2% = 59,8%
Top segment kumulativ procentdel = 59,8% + 40,1% = 99,9%

Bemærk, at den samlede kumulative procentdel, som burde være lig med 100%, da den repræsenterer den samlede indkomst, der er tjent af alle arbejdstagere, kun er 99,9%. Dette sker nogle gange på grund af afrunding af tallene.

Disse to tal, procent og kumulativ procent, placeres normalt i en tabel for at lette læsningen:

Lorenzkurver og Gini-koefficienter

Selv om dataene for procent og kumulativ procent kan give en grov idé om, hvor lige eller ulige indkomstfordelingen er, er det nogle gange nemmere at se, hvordan de står på linje på en graf, så vi kan få en visuel fornemmelse af indkomstlighed. For at gøre dette kan du plotte ud, hvor meget hvert af befolkningsgrupperne tjener (kumulativt), og sammenligne den resulterende kurve med en perfekt lige indkomstfordeling, som ville være en retlinet graf:

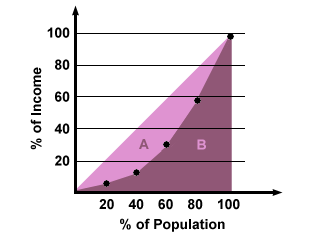
Denne type graf, der viser indkomstfordelingen mellem befolkningssegmenter, kaldes en Lorenz-kurve. Ved hjælp af Lorenz-kurven kan vi også generere en numerisk repræsentation af indkomstlighed kaldet Gini-koefficienten. Gini-koefficienten, som ligger mellem 0 og 1, er lig med arealet mellem den faktiske og den lige fordelingskurve divideret med det samlede areal under den lige fordelingskurve. I figuren ovenfor er Gini-koefficienten lig med arealet af A divideret med arealet af (A + B). Jo større Gini-koefficienten er, jo større er graden af indkomstulighed. En fuldstændig lige indkomstfordeling vil have en Gini-koefficient på 0, mens en fuldstændig ulige fordeling vil have en Gini-koefficient på 1.

Indkomstmobilitet

En anden faktor, der skal tages i betragtning, når man undersøger graden af ulighed i et samfund, er omfanget af indkomstmobilitet. Indkomstmobilitet henviser til den lethed, hvormed arbejdstagere kan bevæge sig op og ned i indkomsthierarkiet. Hvis de rige altid forbliver rige, og de fattige altid forbliver fattige, så er en ulige indkomstfordeling et permanent og alvorligt problem. Hvis arbejdstagerne imidlertid let skifter fra middelklasse til overklasse eller fra underklasse til middelklasse, bliver graden af ulighed mindre alvorlig, da uligheden er flydende og midlertidig (på et individuelt grundlag).