Hvorfor er 0,999… lig med 1?!

En anden måde at tænke på udtrykkene i vores summering er, at hvert efterfølgende udtryk fås ved at gange det foregående udtryk med et fælles forhold.

Det betyder, at vi har en geometrisk serie, der konvergerer mod a/(1 – r), hvor a er den første værdi i serien, og r er det forhold, som vi multiplicerer med for at få det næste udtryk.

Konvergens i en serie betyder simpelthen, at serien vil fortsætte med at komme tættere og tættere på en bestemt værdi, efterhånden som man tilføjer flere og flere termer til serien. Serien kommer uendeligt tæt på konvergensværdien. På en uendelig skala bliver konvergens til lighed.

I vores tilfælde starter vi med 1/10 og multiplicerer med 1/10 hver gang, så både a og r = 1/10.

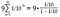
Fuldfør aritmetikken på højre side.

Nu har vi formelt vist, at 0.999…. konvergerer til eller er lig med 1.

Sluttanker & Inspiration

Hvis dette føles mærkeligt for dig, så er det godt! Du ved, at to forskellige tal, i virkeligheden burde være forskellige tal. Den kontraintuitive karakter af dette problem er en del af det mærkelige, der følger med arbejdet med uendelighed.

Selv i et simpelt problem som dette, bevæger du dig fra grænserne for det, der er håndgribeligt for den menneskelige hjerne, til en skala, der på en måde ligger uden for vores fatteevne. Som begrænsede væsener kan vi gribe fat i forståelsen af begrebet uendelighed eller evighed, men vi kan aldrig virkelig opleve det. Det betyder, at det, som vi ved er sandt i vores begrænsede verden, ofte viser sig at opføre sig anderledes på et uendeligt niveau.

Acceptere overgangen fra let opdagelig og reproducerbar matematik til det, der kun kan testes og forestilles i vores hoveder, er en del af matematikkens skønhed og vidunder.

Så tag ikke dagens lektion for pålydende og træk på skuldrene.

Lad der være et lag af tåge mellem dig og den perfekte forståelse. Lad dit sind blive blæst omkuld af det faktum, at uendeligheden opfører sig mærkeligt. Og lad det få dig til at længes efter mere forståelse og frem for alt mere matematik.

Tak for at læse og gruble over uendeligheden sammen med mig i dag!