” Hvor stor er en E. coli-celle, og hvad er dens masse?

Hvor stor er en E. coli-celle, og hvad er dens masse?

Reader Mode

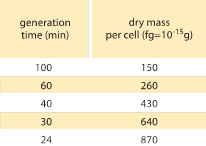
Tabel 1: Sammenhæng mellem bakteriemasse og delingstid. Tørmassen pr. celle er angivet som en funktion af generationstiden (fordoblingstiden). Det foreslås, at massen stiger nogenlunde eksponentielt med væksthastigheden, som oprindeligt observeret af M. Schaechter et al J. Gen. Microbiol., 19:592, 1958. Celletørvægten blev beregnet ved hjælp af en værdi på 173 µg pr. OD460-enhed på 1 mL (BNID 106437). Den anvendte stamme er B/r, en stamme, der almindeligvis anvendes i tidlige bakteriefysiologiske undersøgelser. Værdierne er taget fra F. C. Neidhardt, “Escherichia coli and Salmonella: Cellular and Molecular Biology”, Vol. 1., Chapter 3, ASM Press, 1996.

Størrelsen af en typisk bakterie som E. coli tjener som en praktisk standardlineal til karakterisering af længdeskalaer i molekylær- og cellebiologi. En “tommelfingerregel” baseret på generationer af lys- og elektronmikroskopiske målinger for dimensionerne af en E. coli-celle er at tildele den en diameter på ca. ≈1µm, en længde på ≈2µm og et volumen på ≈1µm3 (1 fL) (BNID 101788). Formen kan tilnærmes som en sfærocylinder, dvs. en cylinder med halvkugleformede hætter. På baggrund af den angivne diameter og længde kan vi beregne et mere raffineret skøn for volumenet på ≈1,3 µm3 (5π/12 for at være nøjagtig). Forskellen mellem denne værdi og den ovenfor anførte tommelfingerregel viser den grad af inkonsekvens, som vi lever komfortabelt med, når vi bruger tommelfingerregler. En af de enkleste veje til et skøn over en bakteries masse er at udnytte volumenet på ≈1 µm3 for en E. coli-celle og antage, at den har samme massefylde som vand. Dette naive skøn resulterer i en anden standardværdi, nemlig at en bakterie som E. coli har en masse på ≈1 pg (pico=10-12). Da de fleste celler består af ca. 2/3 vand (BNID 100044, 105482), og de øvrige bestanddele, som f.eks. proteiner, har en karakteristisk massefylde på ca. 1,3 gange vandets massefylde (BNID 101502, 104272), er omregningen fra cellevolumen til masse nøjagtig med en nøjagtighed på ca. 10 %.

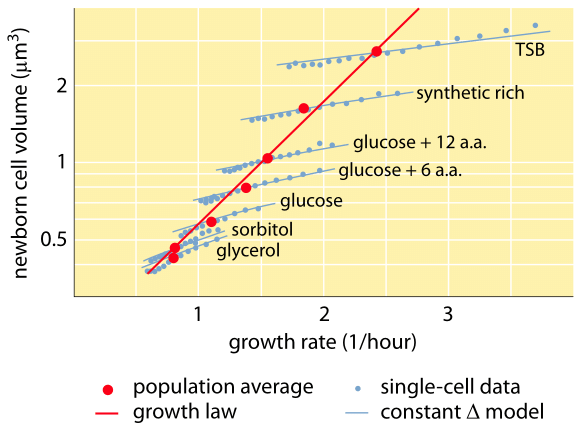
Fig. 1: Sammenhæng mellem cellevolumen og vækstrate. Ved hjælp af mikroskopi og mikrofluidiske anordninger kan cellevolumen måles på enkeltcelleniveau under forskellige betingelser, hvilket bekræfter, at det gennemsnitlige cellevolumen vokser eksponentielt med vækstrate. Derimod varierer variationen mellem cellerne under en given betingelse forskelligt. Variationen i enkeltcellers adfærd anvendes til at teste modeller for regulering af cellestørrelse. (Tilpasset fra S. Taheri-Araghi et al., Curr. Biol. 25:385, 2015.)

Et af de klassiske resultater inden for bakteriefysiologi understreger, at plasticiteten i cellers egenskaber stammer fra afhængigheden af cellemassen af væksthastigheden. Sagt enkelt, hurtigere vækstrater er forbundet med større celler. Denne observation henviser til fysiologiske ændringer, hvor medier, der øger væksthastigheden, også giver større celler, som vist i figur 1. Dette viste sig også at gælde genetisk, hvor langsigtede eksperimentelle udviklingsundersøgelser, der førte til hurtigere vækstrater, viste større cellevolumener (BNID 110462). Sådanne observationer hjælper os med at aflive myten om “cellen” – hvor folk, ofte ubevidst, bruger målinger af en celle til at drage konklusioner om andre celletyper eller den samme celletype under andre forhold. Klassiske undersøgelser af Dennis og Bremer systematiserede disse målinger og fandt, at tørmassen varierer som vist i tabel 1 fra en gennemsnitsværdi på 148 fg for celler, der deler sig hvert 100. minut, til 865 fg for celler med en delingstid på 24 minutter, hvilket indikerer over en 5-dobbelt forskel afhængig af væksthastigheden. En lignende tendens er blevet set i andre organismer (f.eks. for knoppegær, BNID 105103). Ved ca. 70 % vand svarer disse værdier til et interval på mellem ca. 0,4 og 2,5 µm3 med hensyn til volumen. Hvordan kan vi rationalisere de større størrelser for celler, der vokser med højere hastighed? Dette spørgsmål er til debat den dag i dag (Molenaar D. et al. MSB 5:323, 2009; Amir, A., Phys. Rev, Let., 112:208102, 2014). Forklaringer varierer fra at antyde, at det har en fordel i den måde, hvorpå ressourceallokering foregår, til at hævde, at det faktisk kun er en bivirkning af at have en indbygget periode på ca. 60 minutter fra det tidspunkt, hvor en celle beslutter, at den har akkumuleret nok masse til at begynde forberedelserne til deling, og indtil den er færdig med DNA-replikation og delingshandlingen. Denne nogenlunde konstante “forsinkelsesperiode” fører til en eksponentiel afhængighed af den gennemsnitlige cellemasse af væksthastigheden i dette ræsonnement (Amir, A., Phys. Rev, Let, 112:208102, 2014).

Metoder til måling af cellevolumen spænder fra brugen af en Coulter-tæller ((BNID 100004), som udleder volumen baseret på ændringer i modstanden i en lille åbning, når en celle passerer i den, til mere direkte målinger ved hjælp af fluorescensmikroskopi, der måler cellelængder og diametre under forskellige forhold (Figur 1 og BNID 106577, 111480). Det er overraskende, at det forhold, at forskellige laboratorier ikke altid konvergerer om de samme værdier, kan skyldes forskelle i kalibreringsmetoder eller nøjagtige stammer og vækstbetingelser. En hidtil uset evne til at måle cellemassen opnås ved effektivt at veje celler på en mikroskopisk cantilever. Som illustreret i figur 2A anvendes væskestrøm til at tvinge en celle frem og tilbage i den udhulede cantilever. Ved målingen udnyttes det faktum, at cellens masse påvirker cantileverens svingningsfrekvens. Denne frekvens kan måles med en fænomenal nøjagtighed og bruges til at udlede masserne med femtograms nøjagtighed. Ved at ændre væskestrømningsretningen fastholdes cellen i minutter eller mere, og dens masseakkumuleringshastighed måles kontinuerligt på enkeltcelleniveau. Ved den første anvendelse af denne teknik blev det vist, at enkeltceller, der er større, også akkumulerer masse hurtigere, hvilket kaster lys over et længe stillet spørgsmål: Er cellevækst lineær med tiden eller mere passende beskrevet ved en omtrent eksponentiel tendens? Forskellene kan være meget små, men med disse revolutionerende muligheder blev det tydeligt vist, at sidstnævnte scenario bedre repræsenterer situationen i flere af de testede celletyper, som vist i figur 2B.

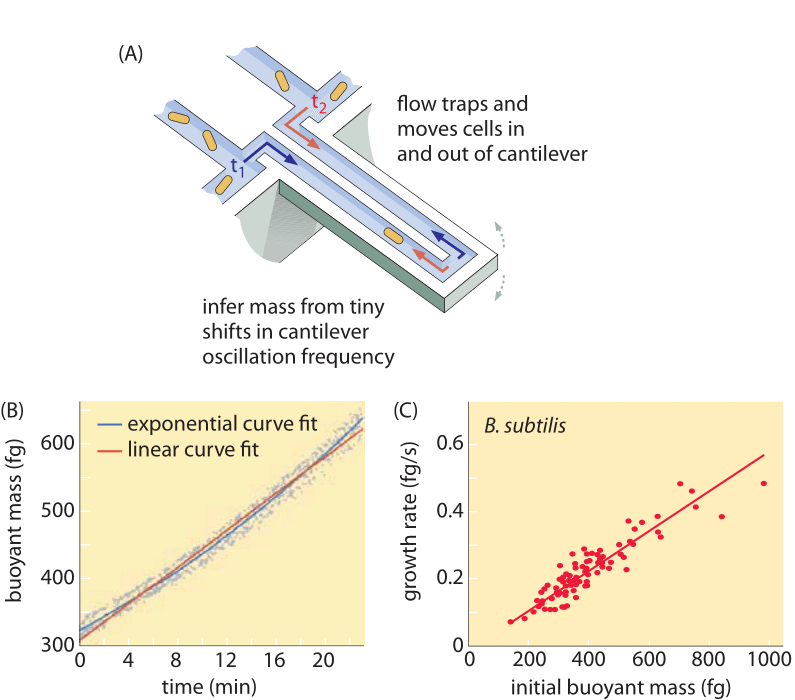
Figur 2: Brug af opdriftsmasse til måling af enkeltcellers vækst. (A) En cantilever i mikronskala svinger med høj frekvens, og cellernes masse kan bestemmes ud fra ændringer i svingningsfrekvensen. (B) Målt over tid resulterer dette i en kurve for akkumulering af enkeltcellers masse som vist. (C) Her er vist B. subtilis-celler. En sammenligning mellem forudsigelserne af de lineære og eksponentielle vækstmodeller er vist som bedste tilpasning. Ligheden viser, hvor tæt de to modeller ligger på hinanden over et område med en kun to gange større stigning i løbet af cellecyklussen. Cellens tørvægt er ca. 4 gange den opdriftsgivende masse. (Tilpasset fra M. Godin et al., Nature Meth. 7:387, 2010.)