Hvad sker der, hvis dine data IKKE er normale?
On januar 15, 2022 by adminI denne artikel diskuterer vi Chebyshevs grænse for statistisk dataanalyse. Hvis man ikke har nogen idé om et givet datasæts normalitet, kan denne grænse bruges til at måle koncentrationen af data omkring middelværdien.
Introduktion
Det er Halloween-uge, og mellem tricks og godbidder griner vi datanørder over dette søde meme over de sociale medier.

Tænker du, at dette er en joke? Lad mig fortælle jer, at det er ikke noget at grine af. Det er skræmmende, helt i Halloween-ånden!
Hvis vi ikke kan antage, at de fleste af vores data (af forretningsmæssig, social, økonomisk eller videnskabelig oprindelse) i det mindste tilnærmelsesvis er “normale” (dvs. de er genereret af en Gauss-proces eller af en sum af flere sådanne processer), så er vi dødsdømt!
Her er en ekstremt kort liste over ting, der ikke vil være gyldige,
- Hele begrebet six-sigma
- Den berømte 68-95-99,7-regel
- Det ‘hellige’ begreb p=0,05 (kommer fra 2 sigma-interval) i statistisk analyse
Skræmmende nok? Lad os tale mere om det…
Den almægtige og allestedsnærværende normalfordeling
Lad os holde dette afsnit kort og godt.
Normalfordelingen (gaussisk) er den mest kendte sandsynlighedsfordeling. Her er nogle links til artikler, der beskriver dens styrke og brede anvendelighed,
- Hvorfor dataloger elsker Gaussian
- Sådan dominerer du statistikdelen af dit interview om datalogi
- Hvad er så vigtigt ved normalfordelingen?
På grund af dens forekomst i forskellige domæner og det centrale grænseteorem (CLT) indtager denne fordeling en central plads inden for datalogi og analytik.
Så, hvad er problemet?
Det er alt sammen helt fint, hvad er problemet?
Problemet er, at du ofte kan finde en fordeling for dit specifikke datasæt, som måske ikke opfylder normalitet, dvs. egenskaberne ved en normalfordeling. Men på grund af den overdrevne afhængighed af antagelsen om normalitet er de fleste business analytics-rammer skræddersyet til at arbejde med normalt fordelte datasæt.
Det er næsten indgroet i vores underbevidsthed.
Lad os sige, at du bliver bedt om at opdage tjekke, om en ny batch data fra en eller anden proces (teknik eller forretning) giver mening. Med ‘giver mening’ mener du, om de nye data hører til, dvs. om de ligger inden for ‘det forventede interval’.
Hvad er denne ‘forventning’? Hvordan kvantificeres intervallet?
Automatisk, som om det var styret af en underbevidst drivkraft, måler vi gennemsnittet og standardafvigelsen for stikprøvedatasættet og fortsætter med at kontrollere, om de nye data falder inden for visse standardafvigelser.
Hvis vi skal arbejde med en 95 % konfidensgrænse, så er vi glade for at se dataene falde inden for 2 standardafvigelser. Hvis vi har brug for en strengere grænse, kontrollerer vi 3 eller 4 standardafvigelser. Vi beregner Cpk, eller vi følger six-sigma retningslinjerne for ppm (parts-per-million) kvalitetsniveau.
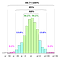
Alle disse beregninger er baseret på den implicitte antagelse, at populationsdataene (IKKE stikprøven) følger Gaussisk fordeling i.Dvs. at den grundlæggende proces, hvorfra alle data er blevet genereret (i fortiden og i nutiden), er styret af mønstret på venstre side.
Men hvad sker der, hvis dataene følger mønstret på højre side?
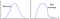
Og, dette, og… det?
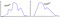
Er der en mere universel grænse, når dataene IKKE er normale?
I sidste ende vil vi stadig have brug for en matematisk forsvarlig teknik til at kvantificere vores konfidensgrænse, selv om dataene ikke er normale. Det betyder, at vores beregning kan ændre sig en smule, men vi bør stadig kunne sige noget i retning af dette-
“Sandsynligheden for at observere et nyt datapunkt i en vis afstand fra gennemsnittet er sådan og sådan…”
Det er klart, at vi skal søge en mere universel grænse end de forkætrede Gauss-grænser på 68-95-99.7 (svarende til 1/2/3 standardafvigelse afstand fra middelværdien).
Godt nok findes der en sådan grænse kaldet “Chebyshev Bound”.
Hvad er Chebyshev Bound, og hvordan er den nyttig?
Chebyshevs ulighed (også kaldet Bienaymé-Chebyshev ulighed) garanterer for en bred klasse af sandsynlighedsfordelinger, at højst en vis brøkdel af værdierne kan være mere end en vis afstand fra middelværdien.
Specifikt kan ikke mere end 1/k² af fordelingens værdier være mere end k standardafvigelser væk fra middelværdien (eller tilsvarende, mindst 1-1/k² af fordelingens værdier ligger inden for k standardafvigelser fra middelværdien).
Det gælder for stort set ubegrænsede typer af sandsynlighedsfordelinger og fungerer ud fra en langt mere afslappet antagelse end normalitet.
Hvordan virker det?
Selv om du ikke ved noget om den hemmelige proces bag dine data, er der en god chance for, at du kan sige følgende,
“Jeg er sikker på, at 75 % af alle data bør falde inden for 2 standardafvigelser væk fra middelværdien”,
Og,
Jeg er sikker på, at 89 % af alle data bør falde inden for 3 standardafvigelser væk fra middelværdien”.
Her er, hvordan det ser ud for en vilkårligt udseende fordeling,

Hvordan anvender man det?
Som du kan gætte dig til nu, behøver den grundlæggende mekanik i din dataanalyse ikke at ændre sig en smule. Du vil stadig indsamle en stikprøve af dataene (jo større jo bedre), beregne de samme to størrelser, som du er vant til at beregne – middelværdi og standardafvigelse, og derefter anvende de nye grænser i stedet for 68-95-99,7-reglen.

Tabellen ser ud som følgende (her betegner k så mange standardafvigelser væk fra middelværdien),

En videodemo af dens anvendelse er her,
Hvad er hagen ved det? Hvorfor bruger folk ikke denne “mere universelle” grænse?
Det er indlysende, hvad fangsten er, hvis man ser på tabellen eller den matematiske definition. Chebyshev-reglen er meget svagere end Gauss-reglen, når det gælder om at sætte grænser for dataene.
Den følger et 1/k²-mønster sammenlignet med et eksponentielt faldende mønster for normalfordelingen.
For eksempel skal man for at afgrænse noget med 95 % sikkerhed medtage data op til 4,5 standardafvigelser mod 4,5 standardafvigelser. kun 2 standardafvigelser (for Normal).
Men det kan stadig redde situationen, når dataene ikke ligner en Normalfordeling.
Er der noget bedre?
Der findes en anden afgrænsning kaldet “Chernoff Bound”/Hoeffding-ulighed, som giver en eksponentielt skarp halefordeling (sammenlignet med 1/k²) for summer af uafhængige tilfældige variabler.
Dette kan også bruges i stedet for den gaussiske fordeling, når dataene ikke ser normale ud, men kun når vi har en høj grad af tillid til, at den underliggende proces er sammensat af delprocesser, som er fuldstændig uafhængige af hinanden.
I mange sociale og forretningsmæssige tilfælde er de endelige data desværre resultatet af et ekstremt kompliceret samspil mellem mange delprocesser, som kan have en stærk indbyrdes afhængighed.
Summary
I denne artikel har vi lært om en særlig type statistisk binding, som kan anvendes på den bredest mulige fordeling af data uafhængigt af antagelsen om normalitet. Dette er praktisk, når vi ved meget lidt om den sande kilde til dataene og ikke kan antage, at de følger en Gaussisk fordeling. Grænsen følger en potenslov i stedet for en eksponentiel natur (som Gaussian) og er derfor svagere. Men det er et vigtigt værktøj at have i sit repertoire til at analysere enhver vilkårlig form for datafordeling.
Skriv et svar