Funktioner eller kortlægning

Nu vil vi i funktioner eller kortlægning studere en særlig form for relation, der kaldes funktioner eller kortlægning. For at forstå dem, skal vi tage nogle få eksempler fra det virkelige liv.

Alle disse spørgsmål har
unikke svar. Lad os
se, hvordan vi kan relatere
dette i læringskortlægning.

● Hvorfra står solen op?

Øst

● Hvilken er hovedstaden i Indien?

Delhi

● Hvad er efterfølgeren til 4?

5

● Hvad er summen af 5 og 3?

8

Afbildning eller funktioner:

Hvis A og B er to ikke-tomme mængder, siges en relation “f” fra mængden A til mængden B at være en funktion eller en afbildning,
● Hvis hvert element i mængden A er forbundet med et unikt element i mængden B.

● Funktionen “f” fra A til B betegnes med f : A → B.

● Hvis f er en funktion fra A til B og x ∈ A, så er f(x) ∈ B, hvor f(x) kaldes billedet af x under f, og x kaldes forbilledet af f(x) under ‘f’.

Note:

For at f er en afbildning fra A til B:

● Ethvert element i A skal have et billede i B. Tilstødende figur repræsenterer ikke en afbildning, da elementet d i mængde A ikke er forbundet med noget element i mængde B.

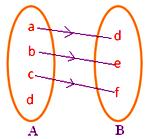
● Intet element i A må have mere end ét billede. Tilstødende figur repræsenterer ikke en afbildning, da element b i mængden A er forbundet med to elementer d, f i mængden B.

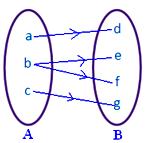
● Forskellige elementer i A kan have det samme billede i B. Tilstødende figur repræsenterer en afbildning.

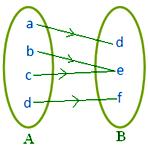
Note:

Alle afbildninger er en relation, men alle relationer er måske ikke nødvendigvis en afbildning.

Funktion som en særlig form for relation:

Lad os minde om og gennemgå funktionen som en særlig form for relation Hvis vi antager, at A og B er to ikke-tomme mængder, så kaldes en regel “f”, der knytter hvert element i A til et unikt element i B, en funktion eller en afbildning fra A til B.
Hvis ‘f’ er en afbildning fra A til B,

udtrykker vi det som f: A → B

læser vi det som ‘f’ er en funktion fra A til B.
Hvis ‘f ‘ er en funktion fra A til B og x∈A og y∈B, så siger vi, at y er billedet af element x under funktionen ‘ f ‘ og betegner det med f(x).
Derfor skriver vi det som y = f(x)

Her kaldes element x for-billedet af y.

Så for en funktion fra A til B.
● A og B skal være ikke-tomme.

● Hvert element i A skal have et billede i B.

● Intet element i “A” skal have mere end ét billede i “B”.
Note:

● To eller flere elementer i A kan have samme billede i B.

● f : x → y betyder, at under funktionen ‘f’ fra A til B har et element x i A billede y i B.

● Det er nødvendigt, at ethvert f-billede er i B, men der kan være nogle elementer i B, som ikke er f-billeder af noget element i A.

● Relationer og afbildning

Ordnet par

Kartesisk produkt af to mængder

Relation

Domæne og rækkevidde af en relation

Funktioner eller afbildning

Domæne Co-domæne og rækkevidde af funktion

● Relationer og kortlægning – Arbejdsark

Arbejdsark om matematiske relationer

Arbejdsark om funktioner eller kortlægning

matematikopgaver for 7. klasse

matematikøvelse for 8. klasse
Fra funktioner eller kortlægning til HJEMMESIDE