Datastrukturer: Stakke og køer – Designveloper

Hvorfor stakke og køer?

I modsætning til et array er der i stakke og køer ingen tilfældig adgang (vi kan ikke få adgang til et element direkte med et ‘indeks’). Vi har normalt færre metoder/handlinger, som vi kan udføre på som f.eks. push(), pop(), peek(), enqueue(), dequeue(), som alle udelukkende omhandler elementet i begyndelsen eller slutningen af datastrukturen.

Men…

Spørgsmål: Dette lyder så begrænsende, da vi kun kan få adgang til det første eller det sidste element i datastrukturen. Hvorfor skulle vi nogensinde ønske at bruge noget som dette? Hvorfor bruger vi ikke bare arrays for at få mere fleksibilitet?

Svar: Stakke og køer er normalt “datastrukturer på højere niveau”, der er bygget oven på datastrukturer på lavere niveau (array eller linked list) for at begrænse de operationer, vi kan udføre på dem. Det er en fordel, hvis vi ønsker begrænset adgang.

Det er en fordel at have denne begrænsede evne på en datastruktur, fordi vi kan kontrollere, hvem der bruger denne datastruktur, som kun udfører rigtige operationer, der er effektive. Vi behøver f.eks. ikke at spekulere på, om nogen tilfældigt har indsat et element midt i vores liste og dermed ødelagt nogle invarianter. Det sparede os for en masse problemer. Lad os se nærmere på dem.

Hvad er en stak?

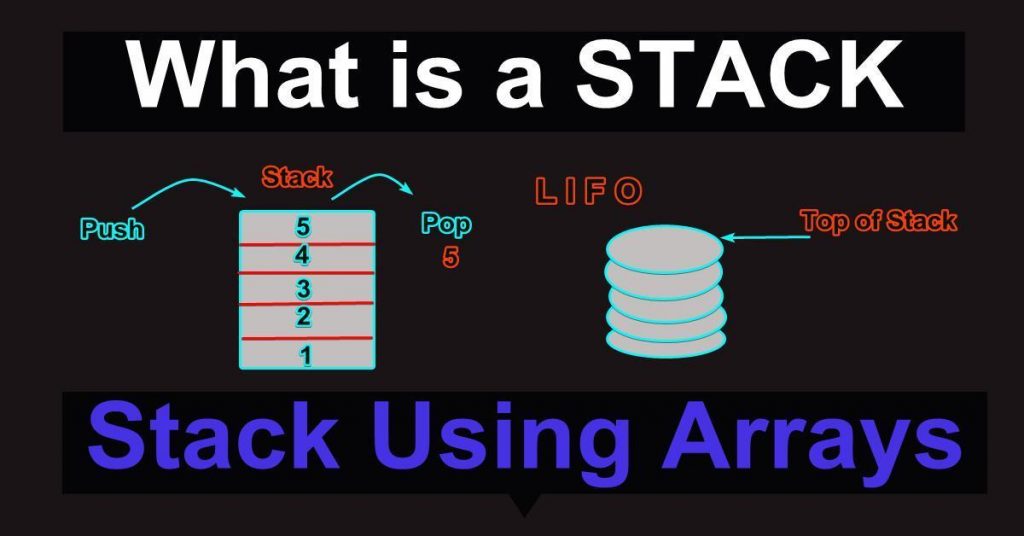
En stak er en lineær datastruktur med én ende, der modellerer en stak i den virkelige verden ved at have to primære operationer, nemlig push og pop.

I dette billede nedenfor kunne vi se, at et dataelement bliver poppet fra toppen af stakken, og et andet bliver tilføjet til den. Der er en top pointer, der peger på blokken øverst på stakken. Dette skyldes, at elementer i en stak altid bliver fjernet og tilføjet til toppen af stakken. Denne adfærd er almindeligvis kendt som LIFO (Last In First Out).

Stack-operationer

Følgende er de 2 grundlæggende operationer, der kan udføres på en stak.

• Push-funktion: Tilføj et element øverst på stakken
• Pop-funktion: Fjern det øverste element (og returnerer det eventuelt)

Visualisering af stakkens grundlæggende operationer

Dertil kommer følgende yderligere funktioner for en stak for at kontrollere dens status.

• Peek-funktion: Returnerer det øverste element i stakken uden at fjerne eller slette det
• isEmpty-funktion: Kontroller, om stakken er tom eller ej
• isFull-funktion: Kontroller, om stakken er tom eller ej
• isFull-funktion: Kontroller, om stakken er fuld eller ej

Alle funktioner opererer på toppen af stakken. Vi har ikke adgang til andet end toppen. Dette er afgørende for at forstå, hvordan den fungerer.

Kompleksitetsanalyse

Den følgende kompleksitetstabel forudsætter, at du har implementeret en stack ved hjælp af en linked list

Stacks anvendelser

Hvornår og hvor bruges en stack? Vi bruger Stack meget i programmering uden at bemærke det, her er nogle eksempler:

• Kan bruges til evaluering af udtryk (f.eks.: en shunting-yard-algoritme til parsing og evaluering af matematiske udtryk).
• Kan bruges til at implementere funktionskald i rekursionsprogrammering.

• Anvendes af fortrydelsesmekanismer i tekstredigeringsprogrammer til at fortryde tekst, som vi har skrevet (Cmd + Z på Mac OS og Ctrl + Z på Windows)
• Anvendes i browseren til at navigere baglæns og fremad
• Kan bruges til at foretage en DFS (Depth First Search) på en graf
• Bruges bag kulisserne til at understøtte rekursion ved at holde styr på tidligere funktionskald

Hvad er en kø?

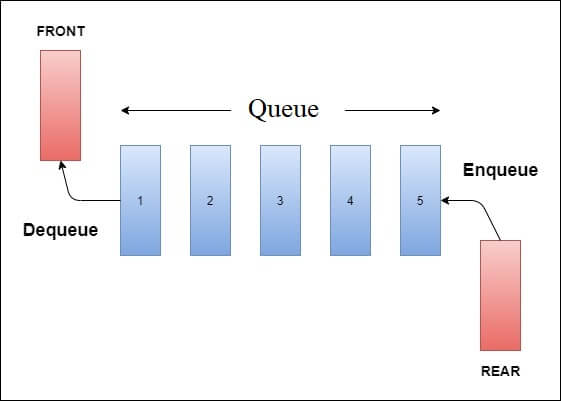
En kø er også en lineær datastruktur, der modellerer køer i den virkelige verden ved at have to primære operationer, nemlig enqueue (vi kan tænke på det som “gå ind i køen”) og dequeue (vi kan også tænke på det som “slette fra køen”). Denne struktur hedder “queue”, fordi den ligner en kø i den virkelige verden – (hvor folk venter i en kø).

Alle køer har en forreste og en bageste ende (nogle gange kaldet “rear”). Vi indsætter elementer gennem bagsiden og fjerner dem gennem forsiden.

En kø er en FIFO-struktur (First In First Out – det element, der er placeret først, kan tilgås først), som almindeligvis findes i mange programmeringssprog.

Køoperationer

Følgende er de 3 grundlæggende operationer, der kan udføres på en kø.

• Enqueue-funktion: Tilføj et element til enden af køen
• Dequeue-funktion: Fjern et element fra begyndelsen af køen
• Peeking-funktion: Kigger på værdien forrest i køen uden at fjerne den

Kompleksitetsanalyse

Som vi kan se på billedet, tager enqueuing- og dequeuing-operationer konstant tid O(1). Imidlertid er kontrollen af, om et element er indeholdt i køen, lineær tid O(n), da vi potentielt ville være nødt til at scanne alle elementerne igennem.

Der er også fjernelse af elementer (ikke dequeuing) internt. Det kræver lineær tid, da vi i værste fald skal scanne alle elementer igennem.

Køapplikationer

• Bruges til at styre tråde i multithreading.
• Kan bruges til effektivt at holde styr på de x senest tilføjede elementer
• Håndtering af webserveranmodninger, hvor vi ønsker først til mølle. For eksempel: På et hvilket som helst tidspunkt kan vores webserver kun betjene op til maksimalt 50 personer samtidigt.

Hvis der kommer 70 anmodninger ind på kort tid, vil vi ikke kunne behandle dem alle. Så webserveren popper kun 50 anmodninger fra køen og sætter de resterende 20 i venteposition. Når webserveren er færdig med at behandle en anmodning, fjerner den den næste anmodning, som den skal betjene, og det bliver den ved med, indtil køen er tom.

• Breadth-first search (BFS) graph traversal
• Bruges til at implementere køsystemer (f.eks.: prioritetskøer)
• Bruges i netværksprintere: Printeren kan kun betjene en enkelt anmodning ad gangen. Så hvis der kommer andre anmodninger, når printeren er optaget, vil det program, der administrerer printeren, ikke afvise disse anmodninger, men sætte dem i en kø, der venter på at blive udført. Den første anmodning vil blive betjent først (FIFO).

Vi håber, at denne artikel har givet dig et billede af stakke og køer i tankerne. Glem ikke at abonnere på vores blog og følg Designveloper på Facebook, Twitter og LinkedIn.

Og disse er andre artikler, du måske vil kunne lide:

• Hvad er webapplikationsarkitektur?
• Datastrukturer og deres anvendelser
• Hvad er Big O Notation?