Cirklens omkreds – Forklaring og eksempler

Vi så før, hvordan man finder omkredsen af en polygon. Vi ved, at cirklen ikke er en polygon, og at den derfor ikke bør have en omkreds. Vi bruger en tilsvarende form for en cirkel, kaldet omkreds.

I denne artikel vil vi diskutere, hvordan man finder omkredsen af en cirkel, omkredsformel og eksempelopgaver om omkredsen af en cirkel.

Hvad er omkredsen af en cirkel?

Afstanden omkring en polygon som f.eks. en firkant eller et rektangel kaldes omkredsen (P). På den anden side kaldes afstanden omkring en cirkel for omkredsen (C). Omkredsen af en cirkel er derfor den lineære afstand til en kant af cirklen.

Hvorfor har vi brug for at beregne omkredsen af en cirkel?

Det er vigtigt at finde omkredsen af et objekt i følgende scenarier:

Hvad enten du vil købe en bh, bukser eller trøje, skal du kende afstanden omkring din talje eller dit bryst. Selv om din krop ikke er en perfekt cirkel, skal du måle dens omkreds ved hjælp af et målebånd. Skræddere bruger for det meste denne teknik til at bestemme omkredsen af en kjole.

Du skal også kende omkredsen af en cirkel, når du laver håndværk, sætter hegn omkring dit spabad eller bare løser en matematikopgave i skolen.

Hvordan finder man omkredsen af en cirkel?

Som tidligere nævnt er omkredsen eller omkredsen af en cirkel afstanden omkring en cirkel eller en hvilken som helst cirkelform. Omkredsen af en cirkel er det samme som længden af en lige linje, der er foldet eller bøjet for at danne cirklen. Omkredsen af en cirkel måles i meter, kilometer, yards, tommer osv.

Der er to måder at finde omkredsens omkreds eller omkreds af en cirkel på. Den første formel indebærer, at man bruger radius, og den anden indebærer, at man bruger diameteren af en cirkel. Det er vigtigt at bemærke, at begge de to metoder giver det samme resultat.

Lad os tage et kig.

Omkredsen af en cirkel er givet ved;

C = 2 * π* R = 2πR

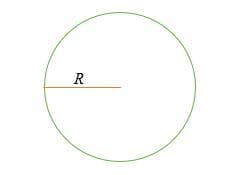
hvor,

C = omkreds eller omkreds,

R = en cirkels radius,

π = den matematiske konstant kaldet Pi

eller

C = π* D = π D

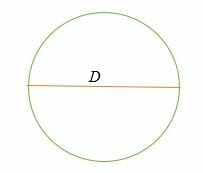
hvor D = 2R = diameteren af en cirkel

For enhver cirkel er forholdet mellem omkredsen og diameteren lig med en konstant kaldet pi.

Omkreds/Diameter = Pi

C /D = Pi eller C/2R = pi

Den omtrentlige værdi af pi (π) = 22/7 = 3,1415926535897…. (en værdi uden ende)

For at gøre det lettere at beregne omkredsen af en cirkel er værdien af pi 3,14 (π = 3,14).

Lad os se et par eksempler nedenfor for at finpudse begrebet omkreds.

Eksempel 1

Find omkredsen af cirklen med en radius på 8 cm.

Løsning

Cirkelomkreds = 2 * π* R = 2πR

= 2 * 3,14 * 8

= 50,24 cm.

Eksempel 2

Beregn omkredsen af en cirkel, hvis diameter er 70 mm

Løsning

Omkreds = π* D = π D

= 3,14 * 70

= 219.8 mm

Eksempel 3

Beregne omkredsen af en cirkulær blomsterhave, hvis radius er 10 m.

Løsning

Omkreds = 2 * π* R = 2πR

= 2 * 3,14 * 10

= 62,8 m.

Eksempel 4

Omkredsen af en cirkel er 440 yards. Find cirklens diameter og radius.

Løsning

Cirkelomkreds = 2 * π* R = 2πR

440 =2 * 3,14 * R

440 = 6.28R

Divider begge sider med 6,28 for at få,

R = 70,06

Dermed er cirklens radius 70,06 yards. Men da diameteren er det dobbelte af cirklens radius, er diameteren altså lig med 140,12 yards.

Eksempel 5

Diameteren på hjulene på en cykel er 100 cm. Hvor mange omdrejninger vil hvert hjul foretage for at tilbagelægge en strækning på 157 meter

Løsning

Beregn omkredsen af cyklens hjul.

Omkreds = π D

= 3.14 * 100

= 314 cm

For at få antallet af omdrejninger af hjulet skal du dividere den tilbagelagte afstand med hjulets omkreds.

Vi skal omregne 157 meter til cm, før vi dividerer, så vi ganger 157 med 100 for at få 15700 cm. Derfor,

Antal omdrejninger = 15700 cm/314 cm

= 50 omdrejninger.

Eksempel 6

Et stykke tråd i form af et rektangel med en længde på 100 cm og en bredde på 50 cm klippes og foldes til en cirkel. Beregn omkredsen og radius af den dannede cirkel.

Løsning

Omkredsen af den dannede cirkel = omkredsen af den rektangulære tråd.

Omkreds af et rektangel = 2(L + B)

= 2(100 + 50) cm

= 2 * 150 cm

= 300 cm.

Dermed vil omkredsen af cirklen være 300 cm.

Beregn nu cirklens radius.

Cirkelomkreds = 2 π R

300 cm = 2 * π * R

300 cm = 2 * 3,14 * R

300 cm = 6,28R

Divider begge sider med 6,28.

R = 47.77 cm

Cirkelens radius vil altså være 47,77 cm.

Eksempel 7

Radius på hvert hjul på en motorcykel er 0,85 m. Hvor langt vil motorcyklen bevæge sig, hvis hvert hjul har 1000 omdrejninger. Antag, at motorcyklen bevæger sig på en lige linje.

Løsning

Find først hjulets omkreds.

Omkreds = 2 π R

= 2 * 3,14 * 0,85

= 5,338 m.

For at finde den tilbagelagte afstand skal hjulets omkreds ganges med antallet af omdrejninger, der foretages.

Distance = 5,338 * 1000

= 5338 m

Dermed er den tilbagelagte distance lig med 5,338 kilometer.

Praksisnære spørgsmål

1. Der serveres en pizza på 12 tommer for Mike og hans venner. Mike er interesseret i at beregne dens omkreds. Hjælp ham!
3. Omkredsen af et bestemt kvadrat er 1/3 af arealet af en bestemt cirkel. Hvis længden af kvadratet er L enheder, så bestem cirklens diameter ud fra L.

Svar

1. 12π tommer eller 37,67 tommer
2. 12L/π enheder

Forrige lektion | Forside | Næste lektion | Næste lektion