2.12: Van der Waals’ ligning

En ligning, der skyldes van der Waals, udvider den ideelle gasligning på en enkel måde. Van der Waals’ ligning er

\

Den passer bedre til tryk-volumen-temperaturdata for en virkelig gas end idealgasligningen gør. Den forbedrede tilpasning opnås ved at indføre to parametre (benævnt “\(a\)” og “\(b\)”), som skal bestemmes eksperimentelt for hver gas. Van der Waals’ ligning er særlig nyttig i vores bestræbelser på at forstå virkelige gassers adfærd, fordi den giver et simpelt fysisk billede af forskellen mellem en virkelig gas og en idealgas.

Ved afledning af Boyles lov fra Newtons love antager vi, at gasmolekylerne ikke interagerer med hinanden. Simple argumenter viser, at dette kun kan være nogenlunde sandt. Reelle gasmolekyler må interagere med hinanden. På korte afstande frastøder de hinanden. På lidt længere afstande tiltrækker de hinanden. Den ideelle gasligning kan også udledes af de grundlæggende antagelser, som vi gør i § 10, ved en anvendelse af teorien om statistisk termodynamik. Ved at gøre forskellige antagelser om molekylære egenskaber kan vi anvende statistisk termodynamik til at udlede\({}^{5}\) van der Waals’ ligning. De nødvendige antagelser er, at molekylerne optager et endeligt volumen, og at de tiltrækker hinanden med en kraft, der varierer som den inverse af en potens af afstanden mellem dem. (Den tiltrækkende kraft antages normalt at være proportional med \(r^{-6}\).)

For at erkende, at virkelige gasmolekyler både tiltrækker og frastøder hinanden, skal vi blot huske, at enhver gas kan gøres flydende ved at sænke dens temperatur og øge det tryk, der påføres den. Hvis vi afkøler væsken yderligere, fryser den til et fast stof. Nu er to kendetegn ved et fast stof, at det bevarer sin form, og at det er næsten inkompressibelt. Vi tilskriver et fast stofs inkompressibilitet til de repulsive kræfter mellem dets molekyler, som er kommet så tæt på hinanden, at de repulsive kræfter mellem dem har fået betydning. For at komprimere det faste stof skal molekylerne skubbes endnu tættere sammen, hvilket kræver en uforholdsmæssig stor kraft. Hvis vi på den anden side kaster en isterning tværs over rummet, flyver alle de vandmolekyler, som den består af, sammen tværs over rummet. Det er tydeligt, at vandmolekylerne i det faste stof tiltrækkes af hinanden, ellers ville de alle gå hver til sit – at kaste isterningen ville være som at kaste en håndfuld tørt sand. Men vandmolekyler er de samme molekyler uanset temperatur og tryk, så hvis der er tiltræknings- og frastødningskræfter mellem dem i det faste stof, må disse kræfter også være til stede i væske- og gasfasen.

I gasfasen er molekylerne langt fra hinanden; i væske- eller faststoffasen er de tæt pakket sammen. Ved kogepunktet er volumenet af en væske meget mindre end volumenet af den gas, som den er kondenseret fra. Ved frysepunktet er volumenet af et fast stof kun lidt forskelligt fra volumenet af den væske, som det er frosset ud fra, og det er helt sikkert større end nul. Disse almindelige observationer kan let forklares ved at antage, at ethvert molekyle har et karakteristisk volumen. Vi kan forstå, at dette igen er en konsekvens af de intermolekylære kræfters natur; det er klart, at disse kræfter bliver stærkere, når afstanden mellem et par molekyler mindskes. Da en væske eller et fast stof har et bestemt volumen, må den frastødende kraft stige hurtigere end den tiltrækkende kraft, når den mellemmolekylære afstand er lille. Ofte er det nyttigt at tale om en kondenseret fases molare volumen. Ved molært volumen forstås volumenet af et mol af et rent stof. Det molare volumen af en kondenseret fase bestemmes af den intermolekylære afstand, hvor der er balance mellem intermolekylære tiltræknings- og frastødningskræfter.

Det er klart, at molekyler er meget tæt på hinanden i kondenserede faser. Hvis vi antager, at de tomme rum mellem molekylerne er ubetydelige, er volumenet af en kondenseret fase omtrent lig med antallet af molekyler i prøven ganget med volumenet af et enkelt molekyle. Det molære rumfang er så Avogadros tal gange det rumfang, som et molekyle optager. Hvis vi kender densiteten, D, og den molære masse, \(\overline{M}\), kan vi finde det molære volumen, \(\overline{V}\), som

Det volumen, der optages af et molekyle, V\({}_{molecule}\), bliver

\

Det tryk og volumen, der fremgår af van der Waals’ ligning, er den virkelige gas’ tryk og volumen. Vi kan relatere termerne i van der Waals’ ligning til den ideelle gasligning: Det er nyttigt at betragte udtrykkene \(\left(P+{{{{an}^2}/{V^2}\right)\) og \(\left(V-nb\right)\) som trykket og volumenet for en hypotetisk idealgas. Det vil sige

\ &=nRT \end{align*}}]

Så har vi

\

Vi udleder den ideelle gasligning fra en model, hvor molekylerne er ikke-interagerende punktmasser. Så volumenet af en idealgas er det volumen, der optages af en gas, hvis individuelle molekyler har et volumen på nul. Hvis de enkelte molekyler i en virkelig gas effektivt optager et volumen \({b}/{\overline{N}}}\), så optager \(n\) mol af dem effektivt et volumen

\

Van der Waals’ ligning siger, at volumenet af en virkelig gas er det volumen, der ville være optaget af ikke-interagerende punktmasser, \(V_{{ideal\ gas}}\), plus det effektive volumen af selve gasmolekylerne. (Når data for virkelige gasmolekyler tilpasses van der Waals’ ligning, er værdien af \(b\) normalt noget større end det volumen, der skønnes ud fra væsketætheden og molekylvægten. Se problem 24.)

Sådan har vi

Vi kan forstå dette som en logisk konsekvens af tiltrækkende vekselvirkninger mellem molekylerne i den virkelige gas. Med \(a>0\) siger det, at trykket i den reelle gas er mindre end trykket i den hypotetiske ideelle gas, med en mængde, der er proportional med \({\left({n}/{V}\right)}^2\). Proportionalitetskonstanten er \(a\). Da \({n}/{V}\) er den molære massefylde (mol pr. volumenenhed) af gasmolekylerne, er det et mål for koncentrationen. Antallet af kollisioner mellem molekyler af samme art er proportionalt med kvadratet på deres koncentration. (Vi ser nærmere på dette punkt i kapitel 4 og 5.) Så \({{\left({{n}/{V}\right)}^2\) er et mål for den hyppighed, hvormed de virkelige gasmolekyler kommer i nærkontakt med hinanden. Hvis de tiltrækker hinanden, når de kommer tæt på hinanden, bør effekten af denne tiltrækning være proportional med \({\left({{n}/{V}\right)}^2\). Så van der Waals’ ligning er i overensstemmelse med tanken om, at trykket i en virkelig gas adskiller sig fra trykket i den hypotetiske idealgas med et beløb, der er proportionalt med hyppigheden og styrken af tiltrækkende vekselvirkninger.

Men hvorfor skulle tiltrækkende vekselvirkninger have denne effekt; hvorfor skulle trykket i den virkelige gas være mindre end trykket i den hypotetiske idealgas? Måske er den bedste måde at udvikle et kvalitativt billede på at erkende, at tiltrækkende intermolekylære kræfter har en tendens til at få gasmolekylerne til at klumpe sig sammen. Det er trods alt disse tiltrækningskræfter tiltrækningskraft, der får molekylerne til at samle sig til en væske ved lave temperaturer. Over kogepunktet begrænser gasmolekylernes evne til at gå hver sin vej virkningerne af denne tendens; men selv i gassen må de tiltrækkende kræfter virke på en måde, der har tendens til at reducere det volumen, som molekylerne optager. Da det volumen, som gassen optager, er dikteret af beholderens størrelse – ikke af gassens egne egenskaber – kommer denne tendens til sammenklumpning til udtryk som et fald i trykket.

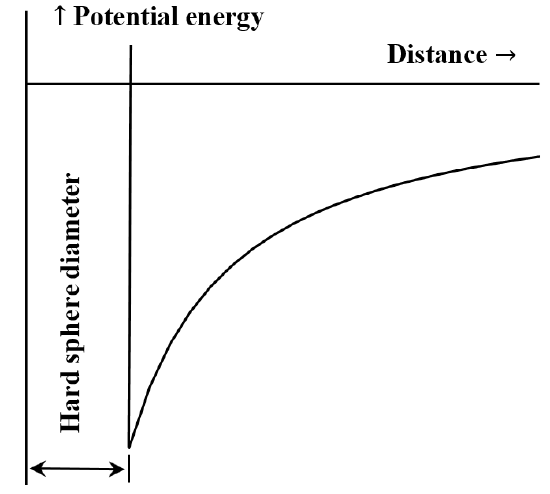
Det er ofte nyttigt at beskrive vekselvirkningen mellem partikler eller kemiske enheder i form af et diagram over potentiel energi versus afstand. Van der Waals’ ligning svarer til det tilfælde, at den frastødende vekselvirkning mellem molekyler er ikke-eksisterende, indtil molekylerne kommer i kontakt med hinanden. Når de først kommer i kontakt, bliver den energi, der kræves for at flytte dem endnu tættere på hinanden, vilkårligt stor. Ofte beskrives dette ved at sige, at de opfører sig som “hårde kugler”. Den tiltrækkende kraft mellem to molekyler aftager i takt med, at afstanden mellem dem øges. Når de er meget langt fra hinanden, er den tiltrækkende vekselvirkning meget lille. Vi siger, at vekselvirkningsenergien er nul, når molekylerne er uendeligt langt fra hinanden. Hvis vi i begyndelsen har to meget adskilte, stationære molekyler, der tiltrækker hinanden gensidigt, vil de spontant bevæge sig hen imod hinanden og få kinetisk energi undervejs. Deres potentielle energi aftager, efterhånden som de nærmer sig hinanden, og når sin mindste værdi, når molekylerne kommer i kontakt med hinanden. Van der Waals’ ligning medfører således det diagram med potentiel energi i forhold til afstanden, der er skitseret i figur 5.