Součet součinu (SOP) a součin součtu (POS)

Součin součtu (POS) & Součet součinu (SOP)

Součet součinu (SOP)

Součet součinu je zkrácený tvar SOP. Forma součtu součinu je forma výrazu v booleovské algebře, ve které se sčítají různé součinové členy vstupů. Tento součin není aritmetickým násobením, ale je logickým booleovským AND a Součet je logickým booleovským OR.

Pro lepší pochopení SOP potřebujeme znát min. termín.

Min. termín

Min. termín znamená termín, který je pravdivý pro minimální počet kombinací vstupů. To znamená, že je pravdivý pouze pro jednu kombinaci vstupů.

Protože hradlo AND také dává True pouze tehdy, když jsou pravdivé všechny jeho vstupy, takže můžeme říci, že min. termíny jsou AND kombinací vstupů jako v tabulce uvedené níže.

3 vstupy mají 8 různých kombinací. Každá kombinace má min. člen označený malým m a jeho desetinné číslo kombinace zapsané v dolním indexu. Každý z těchto minitermů bude pravdivý pouze pro danou kombinaci vstupů.

• Můžete si také přečíst: & Použití

Typy tvarů součtu součinů (SOP)

Existuje několik různých tvarů součtu součinů.

• Kanonická forma SOP
• Nekanonická forma SOP
• Minimální forma SOP

Kanonická forma SOP

Toto je standardní forma součtu součinů. Tvoří ji O Ring mintermů funkce, pro kterou je výstup pravdivý. Je také známá jako Suma mintermů nebo Kanonická disjunktní normální forma (CDNF). Je to jen módní název. „Kanonický“ znamená „normalizovaný“ a „disjunktivní“ znamená „Logický OR sjednocení“.

Kanonický výraz SOP je reprezentován součtovým znaménkem ∑ a mintermy v závorkách, pro které je výstup pravdivý.

Například pravdivostní tabulka funkce je uvedena níže.

Pro tuto funkci je kanonický SOP výraz

F = ∑( m1, m2, m3, m5 )

Což znamená, že funkce je pravdivá pro mintermy {1, 2, 3, 5}.

Rozšířením součtu dostaneme.

F = m1 + m2 + m3 + m5

Nyní dosadíme min členy do výrazu

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

Kanonický tvar obsahuje všechny vstupy buď doplněné, nebo nedoplněné ve svých součinových členech.

Můžete také číst:

Nekanonický tvar SOP

Jak již název napovídá, jedná se o nestandardizovanou formu výrazů SOP. Součinové výrazy nejsou výrazy min, ale jsou zjednodušené. Vezměme si jako příklad výše uvedenou funkci v kanonickém tvaru.

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = A̅B̅C + A̅B(C̅ + C) + AB̅C

F = A̅B̅C + A̅B(1) + AB̅C

F = A̅B̅C + A̅B + AB̅C

Tento výraz je stále ve tvaru součtu součinů, ale je ne-kanonický nebo nestandardizovaný tvar.

Minimální SOP tvar

Tento tvar je nejjednodušší SOP vyjádření funkce. Jedná se rovněž o nekanonickou formu. Minimální formu SOP lze vytvořit pomocí Booleovy algebraické věty, ale velmi snadno ji lze vytvořit pomocí Karnaughovy mapy (K-mapy).

Minimální forma SOP je výhodná, protože používá minimální počet hradel a vstupních řádků. je komerčně výhodná díky své kompaktní velikosti, vysoké rychlosti a nízkým výrobním nákladům.

Uveďme si příklad výše uvedené funkce v kanonickém tvaru.

Její K-mapa je uvedena níže.

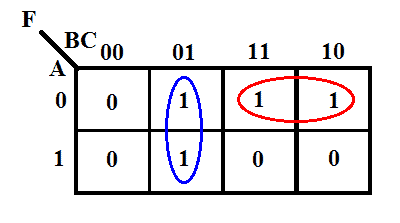
Podle K-mapy bude výstupní výraz

F = B̅C + A̅B

To je nejjednodušší & optimalizovaný výraz pro uvedenou funkci. Tento výraz vyžaduje pouze dvě dvouvstupová hradla AND & jedno dvouvstupové hradlo OR. Kanonický tvar však potřebuje čtyři 3vstupová hradla AND &jedno 4vstupové hradlo OR, což je relativně nákladnější než implementace v minimálním tvaru.

• Můžete si také přečíst: & Johnsonův čítač – konstrukce & Provoz

Schematický návrh součtu součinů (SOP)

Výraz SOP realizuje dvouúrovňové provedení AND-OR, ve kterém je hradlem 1. úrovně hradlo AND následující za hradlem 2. úrovně, které je hradlem OR. Schematický návrh výrazu SOP potřebuje skupinové pole hradel AND & jedno hradlo OR.

Každý výraz SOP má do jisté míry stejné provedení, tj. všechny vstupy procházejí hradlem AND a výstupy těchto hradel AND pak procházejí hradlem OR, jak je znázorněno na obrázku uvedeném níže.

Počet vstupů a počet hradel AND závisí na tom, jaký výraz implementujeme.

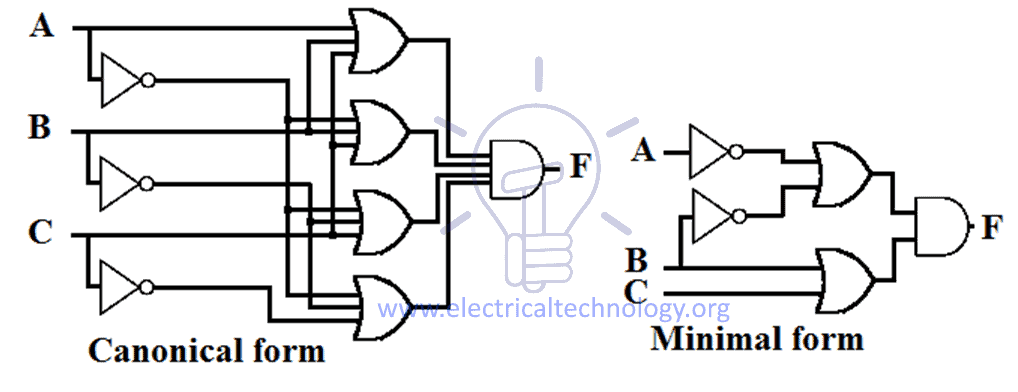
Příklad návrhů kanonického a minimálního SOP výrazu pro funkci je uveden níže.

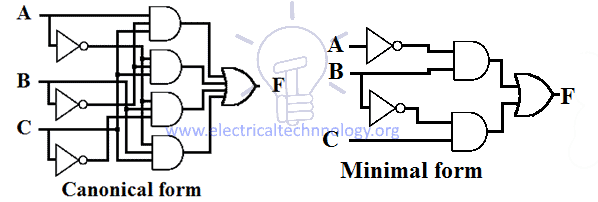
Převod z minimálního SOP na kanonický SOP tvar

Převod z minimálního nebo jakéhokoli nekanonického tvaru na kanonický tvar je velmi jednoduchý.

Jak víme, kanonický tvar má min. členů & min. členy se skládají ze všech vstupů buď doplněných, nebo nedoplněných. Každý člen minimální SOP tedy vynásobíme součtem chybějících vstupů doplněné a nedoplněné formy. Příklad převodu pro výše uvedenou funkci v minimálním tvaru SOP je uveden níže.

Minimální tvar SOP

F = A̅B + B̅C

Termín A̅B je chybějící vstup C. Proto budeme A̅B násobit (C+C̅), protože (C+C̅ = 1). Výraz B̅C je chybějící vstup A. takže bude vynásoben (A+A̅)

F = A̅B(C + C̅) + B̅C(A + A̅)

F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C

Tento výraz je nyní v kanonickém tvaru.

Převod z kanonického SOP na kanonický POS

Standardní výraz SOP lze převést na standardní výraz POS (součin součtu). Například výše uvedená funkce je v kanonickém SOP tvaru

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = ∑ ( m1, m2, m3, m5 )

Zbylé členy této funkce jsou maxtermy, pro které je výstup nepravdivý. Tyto maxtermy jsou M0,M4,M6,M7. Tyto maxtermy budou použity ve výrazu POS jako součin těchto maxtermů. Symbol součinu je ∏.

F = ∏ ( M0, M4, M6, M7)

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

Termíny Max jsou doplňky mintermínů. Proto je M0=(A+B+C).

• Můžete si také přečíst: Převod z kanonické SOP na minimální SOP

  Kanonickou SOP lze převést na minimální SOP. Lze ji převést pomocí Karnaughovy mapy nebo Booleovy algebraické věty. Metoda K-mapy je velmi snadná a její příklad byl proveden výše ve tvaru minimální SOP.

  Součin součtu

  Součin součtu zkráceně POS.

  Součin součtu je tvar, ve kterém se berou součiny různých součtových členů vstupů. Nejedná se o aritmetický součin a součet, ale o logické booleovské AND, respektive OR.

  Pro lepší pochopení Součinu součtu potřebujeme znát pojem Max termín.

  Max termín

  Maxtermem rozumíme termín nebo výraz, který je pravdivý pro maximální počet kombinací vstupů nebo který je nepravdivý pouze pro jednu kombinaci vstupů.

  Protože hradlo OR dává také nepravdu pouze pro jednu kombinaci vstupů. Maxterm je tedy OR buď doplněných, nebo nedoplněných vstupů.

  Maxtermy pro 3 vstupní proměnné jsou uvedeny níže.

  

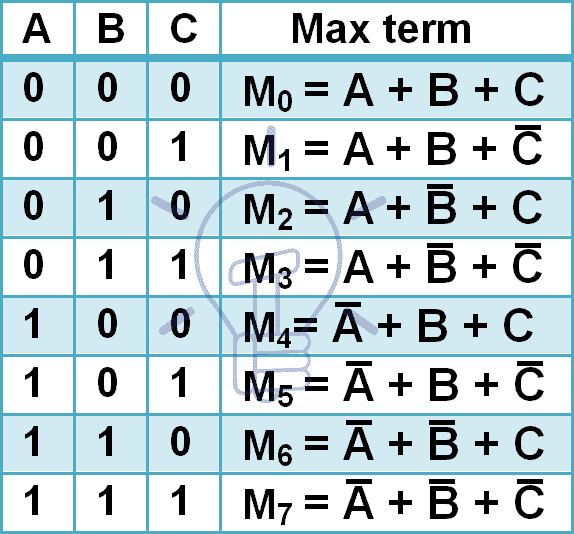
  3 vstupy mají 8 různých kombinací, takže budou mít 8 maxtermů. Maxtermy jsou označeny velkým M a desetinným číslem kombinace V dolním indexu, jak je uvedeno v tabulce uvedené výše.

  V maxtermu je každý vstup doplněn, protože maxterm dává ‚0‘ pouze při použití uvedené kombinace a maxterm je doplňkem mintermu.

  M3 = m̅3

  M3 = (A̅BC)‘

  M3 = A + B̅ +C̅ DE Morganův zákon

  Proto pro A=0 maxterm tvoří A & pro A=1 maxterm tvoří A̅.

  Můžete také číst:

  Typy součinových forem

  Existují různé typy součinových forem.

  • Kanonická forma POS
  • Nekanonická forma
  • Minimální forma POS

  Kanonická forma POS

  Je také známá jako Součin maximálního členu nebo Kanonická konjunktivní normální forma (CCNF). Kanonický znamená normální a konjunktivní znamená průnik.

  V této formě jsou maxtermy, pro které je výstup nepravdivý, AND dohromady.

  Kanonický POS výraz je reprezentován ∏ a maxtermy, pro které je výstup nepravdivý, v závorkách, jak ukazuje příklad uvedený níže.

  

  F = ∏ (M0, M4, M6, M7)

  Rozšíření součinu

  F = M0.M4.M6.M7

  Složení maximálních členů

  F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

  Kanonický tvar obsahuje v každém svém součtovém členu všechny vstupy buď doplněné, nebo nedoplněné.

  • Můžete si také přečíst:
    

    Nekanonický tvar

    Součin součtového výrazu, který není ve standardním tvaru, se nazývá nekanonický tvar.

    Uveďme si jako příklad výše uvedenou funkci.

    F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

    F = (B+C) (A̅+B̅+C)(A̅+B̅+C̅)

    .

    Stejné, ale převrácené členy eliminuje ze dvou Maxových členů a vytvoří jediný člen pro důkaz zde je příklad.

    = (A+B+C) (A̅+B+C)

    = AA̅+AB+AC+A̅B+BB+BC+A̅C+BC+CC

    = 0+AB+AC+A̅B+A̅C+B+BC+C

    = A(B+C)+A̅(B+C)+B(1+C)+C

    .

    = (B+C)(A+A̅)+B(1)+C

    = (B+C)(0)+B+C

    = B+C

    Dosažený výraz je stále ve tvaru Součin součtů, ale je nekanonický tvar.

    Minimální forma POS

    Jedná se o nejvíce zjednodušenou a optimalizovanou formu výrazu POS, která není kanonická. Minimálního součinu součtové formy lze dosáhnout pomocí booleovských algebraických vět jako ve výše uvedeném nekanonickém příkladu. Další metodou dosažení minimální formy POS je použití Karnaughovy mapy, která je relativně jednodušší než použití Booleových algebraických vět.

    Minimální forma POS používá při své implementaci menší počet vstupů a logických hradel, proto se jim dává přednost před kanonickou formou pro jejich kompaktní,rychlou a levnou implementaci.

    Vezměme si jako příklad výše uvedenou funkci

    K-mapa funkce

    

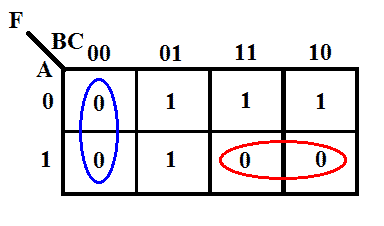
    Minimální vyjádření pomocí K-mapy

    F = (B+C) (A̅+B̅)

    Dosažený výraz je minimální součin součtového tvaru. Je to stále součin součtového výrazu, ale potřebuje pouze 2 vstupy dvě hradla OR a jedno 2 vstupní hradlo AND. Kanonický tvar však potřebuje 4 hradla OR o 3 vstupech a 1 hradlo AND o 4 vstupech.

    • Můžete si také přečíst: Součin součtového výrazu (POS)

      Součin součtového výrazu má specifický schematický návrh OR-AND. V OR-AND vstupy procházejí polem hradel OR, což je první úroveň hradel, výstup z první úrovně hradel OR prochází druhou úrovní hradel,což je hradlo AND.

      Počet vstupů a počet hradel použitých v tomto návrhu závisí na výrazu, který má být realizován.

      Kanonický tvar se skládá z maximálního možného počtu vstupů a hradel,avšak minimální tvar se skládá z nejnižšího možného počtu vstupů a hradel. Schematický návrh kanonické a minimální formy POS je uveden níže.

      

      Převod z minimální formy POS na kanonickou formu POS

      Jak víme, kanonická forma POS má max. členů a max. členů obsahuje každý vstup buď doplněný, nebo nedoplněný. Každý součtový člen tedy doplníme součinem doplněného a nedoplněného chybějícího vstupu. Příklad jeho převodu je uveden níže.

      Minimální forma POS

      F = (A̅+B̅) (B+C)

      (A̅+B̅) člen je chybějící vstup C, takže k němu přidáme (CC̅). (B+C) termínu chybí vstup A, takže k němu přidáme (AA̅).

      F = (A̅+B̅+CC̅) (B+C+AA̅)

      F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)(A̅+B+C)

      Tento výraz je nyní v kanonickém tvaru.

      • Můžete také číst: Součet a typy elektronických čítačů

      Převod z kanonického POS na SOP

      Součinový výraz lze převést na Součinový tvar pouze tehdy, je-li výraz v kanonickém tvaru. Kanonický POS a kanonický SOP jsou vzájemně převoditelné, tj. lze je převádět jeden na druhý. Příklad převodu POS na SOP je uveden níže.

      Kanonický tvar POS

      F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

      V kanonickém tvaru je každý součtový člen maximálním členem, takže jej lze zapsat také jako:

      F = ∏(M0,M4,M6,M7)

      Zbylé kombinace vstupů jsou mintermy funkce, pro které je její výstup pravdivý. Abychom ji převedli na výraz SOP, změníme nejprve symbol na součet (∑) a použijeme zbývající mintermy:

      F = ∑ (m1,m2,m3,m5)

      Nyní rozbalíme znak součtu a vytvoříme kanonický výraz SOP.

      F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

      Min výrazy jsou komplementem Max výrazů pro stejnou kombinaci vstupů.

      Kanonický na minimální POS

      Kanonický součin součtového výrazu lze převést na minimální součin součtového tvaru pomocí Karnaughovy mapy (K-mapy). Další metodou převodu kanonického na minimální je použití Booleovy algebraické věty.

      Použití K-mapy je velmi snadné, proto je K-mapa preferována. Pro minimální výraz POS se 0 v K-mapě spojí do skupin a výraz, který dostaneme, je doplněný, protože skupiny byly vytvořeny z ‚0‘. Jeho příklad byl proveden výše.

      Můžete si také přečíst:

      • Digitální logické hradlo NOT – digitální invertorové logické hradlo
      • Digitální logické hradlo Exclusive-NOR (XNOR)
      • Digitální logické hradlo NOR
      • Digitální logické hradlo NAND

      .