Rozdělení příjmů

Definice a měření rozdělení příjmů

Rozdělení příjmů je plynulost nebo rovnost, s jakou jsou příjmy rozdělovány mezi členy společnosti. Pokud všichni vydělávají přesně stejné množství peněz, pak je rozdělení příjmů dokonale rovnoměrné. Pokud nikdo nevydělává žádné peníze kromě jedné osoby, která vydělává všechny peníze, pak je rozdělení příjmů dokonale nerovnoměrné. Obvykle se však rozdělení příjmů ve společnosti nachází někde uprostřed mezi rovností a nerovností.

Jak tuto míru rovnosti či nerovnosti měříme? Ekonomové často měří rovnost příjmů tak, že zjišťují, kolik příjmů vydělávají různé skupiny obyvatelstva. Pokud například rozdělíme všechny pracující do pěti segmentů podle toho, kolik vydělávají: 20 % nejlepších, 20 % druhých, 20 % třetích, 20 % čtvrtých a 20 % nejnižších, a získáme údaje o tom, kolik peněz vydělávají, můžeme pak vytvořit graf s podrobnými údaji o tom, kolik příjmů vydělává každý segment z celkové výše příjmů všech pracujících. Čím větší je rozdíl mezi jednotlivými segmenty, tím větší je příjmová nerovnost.

Řekněme, že průměrné příjmy pěti segmentů společnosti jsou 10 000, 24 000, 50 000, 80 000 a 110 000 dolarů. Abychom se mohli podívat na rozdělení příjmů, potřebujeme zjistit, kolik procent z celkového příjmu vydělává každý segment, a nikoliv skutečnou částku, kterou každý z nich vydělává. Vzhledem k tomu, že každý ze segmentů je stejně velký, nemusíme se zabývat vážením průměrných příjmů a můžeme provést jednoduchý výpočet podílu na celkových příjmech každého segmentu.

Pro celkový příjem použijeme součet pěti průměrných příjmů:

Celkový příjem = 10000 + 24000 + 50000 + 80000 + 110000
Celkový příjem = 274000

Dále zjistíme procento z celkového příjmu, které vydělává každý segment populace, tak, že vydělíme jeho příjem celkovým příjmem:

Podíl dolního segmentu = 10000/274000 = 0.036 = 3,6 %
Druhý segment procento = 24000/274000 = 0,088 = 8.8 %
Třetí segment procento = 50000/274000 = 0,182 = 18,2 %
Čtvrtý segment procento = 80000/274000 = 0,292 = 29,2 %
Top segment procento = 110000/274000 = 0,401 = 40,1 %

Z těchto údajů vyplývá, že dolní pětina obyvatelstva dostává méně než 4 % celkového příjmu, zatímco horní pětina obyvatelstva dostává více než 40 % celkového příjmu, což svědčí o velké míře nerovnosti příjmů.

Ekonomové se zabývají také kumulativními údaji o rozdělení příjmů. K tomu stačí sečíst procenta na jednotlivých úrovních, čímž získáme výši příjmu všech osob na určité úrovni nebo pod ní. V našem příkladu by to fungovalo takto:

Kumulativní procento dolního segmentu = 3,6 %
Kumulativní procento druhého segmentu = 3,6 % + 8,8 % = 12,4 %
Kumulativní procento třetího segmentu = 12,4 % + 18,2 % = 30,6 %
Kumulativní procento čtvrtého segmentu = 30 %.6% + 29,2% = 59,8%
Vrcholový segment kumulativní procento = 59,8% + 40,1% = 99,9%

Všimněte si, že celkové kumulativní procento, které by mělo být rovno 100%, protože představuje celkový příjem všech pracovníků, je pouze 99,9%. K tomu někdy dochází v důsledku zaokrouhlování čísel.

Tyto dva údaje, procento a kumulativní procento, se pro snazší čtení obvykle uvádějí v tabulce:

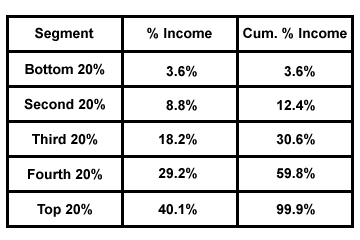
Lorenzovy křivky a Giniho koeficienty

Přestože údaje o procentech a kumulativních procentech mohou poskytnout přibližnou představu o tom, jak rovnoměrné nebo nerovnoměrné je rozdělení příjmů, někdy je snazší vidět, jak jsou seřazeny v grafu, abychom mohli získat vizuální představu o rovnosti příjmů. Za tímto účelem vyneseme do grafu, kolik vydělává každý ze segmentů populace (kumulativně), a výslednou křivku porovnáme s dokonale rovným rozdělením příjmů, což by byl přímkový graf:

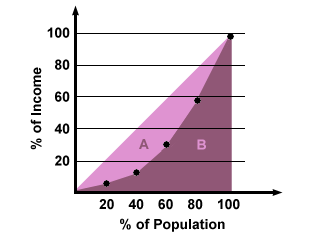
Tento typ grafu, který zobrazuje rozdělení příjmů mezi jednotlivé segmenty populace, se nazývá Lorenzova křivka. Pomocí Lorenzovy křivky můžeme také vytvořit číselné vyjádření rovnosti příjmů, které se nazývá Giniho koeficient. Giniho koeficient, který se pohybuje v rozmezí 0 až 1, se rovná ploše mezi křivkami skutečného a rovného rozdělení vydělené celkovou plochou pod křivkou rovného rozdělení. Na výše uvedeném obrázku se Giniho koeficient rovná ploše A dělené plochou (A + B). Čím větší je Giniho koeficient, tím větší je míra příjmové nerovnosti. Dokonale rovné rozdělení příjmů bude mít Giniho koeficient 0, zatímco dokonale nerovné rozdělení bude mít Giniho koeficient 1.

Mobilita příjmů

Dalším faktorem, který je třeba brát v úvahu při studiu míry nerovnosti ve společnosti, je míra mobility příjmů. Příjmová mobilita označuje snadnost, s jakou se pracovníci mohou pohybovat nahoru a dolů v hierarchii výdělkové síly. Pokud bohatí zůstávají vždy bohatí a chudí vždy chudí, pak je nerovnoměrné rozdělení příjmů trvalým a závažným problémem. Pokud však pracovníci snadno přecházejí ze střední třídy do vyšší třídy nebo z nižší třídy do střední třídy, pak se míra nerovnosti stává méně závažnou, protože nerovnost je plynulá a dočasná (na individuální bázi).

.