Proč se 0,999… rovná 1?!

Jiný způsob, jak uvažovat o členech v našem součtu, je, že každý následující člen získáme vynásobením předchozího členu společným poměrem.

To znamená, že máme geometrickou řadu, která konverguje k a/(1 – r), kde a je první hodnota v řadě a r je poměr, kterým násobíme, abychom získali další člen.

Konvergence v řadě jednoduše znamená, že se řada bude stále více přibližovat k určité hodnotě, jak budeme do řady přidávat další a další členy. Řada se nekonečně blíží hodnotě konvergence. V nekonečném měřítku se konvergence stává rovností.

V našem případě začínáme s číslem 1/10 a pokaždé násobíme 1/10, takže a i r = 1/10.

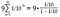
Doplňte aritmetiku na pravé straně.

Teď jsme formálně ukázali, že 0.999… konverguje k 1 nebo se jí rovná.

Závěrečné myšlenky & Inspirace

Pokud vám to připadá divné, je to dobře! Víte, že dvě různá čísla, by ve skutečnosti měla být různá čísla. Protiintuitivní povaha tohoto problému je vlastní podivnosti, která provází práci s nekonečnem.

I v tak jednoduchém problému, jako je tento, se pohybujete z hranic toho, co je pro lidský mozek hmatatelné, na škále, která je svým způsobem mimo naše chápání. Jako konečné bytosti můžeme chápat pojem nekonečna nebo věčnosti, ale nikdy ho nemůžeme skutečně zažít. Což znamená, že se často stává, že to, co známe jako pravdivé v našem konečném světě, se na nekonečné úrovni chová jinak.

Přijetí přechodu od snadno objevitelné a reprodukovatelné matematiky k tomu, co si můžeme vyzkoušet a představit pouze v naší mysli, je součástí krásy a zázraku matematiky.

Neberte tedy dnešní lekci za bernou minci a pokrčte nad ní rameny.

Nechť je mezi vámi a dokonalým pochopením vrstva mlhy. Nech svou mysl vyvanout skutečností, že nekonečno se chová podivně. A nechť to ve vás vyvolá touhu po větším pochopení a především po větším množství matematiky.

Děkuji, že jste si dnes se mnou přečetli a zamysleli se nad nekonečnem!