Obvod kruhu – vysvětlení a příklady

Předtím jsme si ukázali, jak zjistit obvod mnohoúhelníku. Víme, že kruh není mnohoúhelník, proto by neměl mít obvod. Používáme ekvivalentní tvar pro kružnici, který se nazývá obvod.

V tomto článku se budeme zabývat tím, jak zjistit obvod kružnice, vzorcem pro obvod kružnice a příkladovými úlohami o obvodu kružnice.

Co je obvod kružnice?

Vzdálenost kolem mnohoúhelníku, například čtverce nebo obdélníku, se nazývá obvod (P). Naproti tomu vzdálenost kolem kruhu se označuje jako obvod (C). Obvod kruhu je tedy lineární vzdálenost hrany kruhu.

Proč potřebujeme vypočítat obvod kruhu?

Zjištění obvodu objektu je důležité v následujících případech:

Ať už si chcete koupit podprsenku, kalhoty nebo svetr, potřebujete znát vzdálenost kolem pasu nebo hrudníku. Přestože vaše tělo není dokonalý kruh, budete muset změřit jeho obvod pomocí metru. Tuto techniku většinou používají krejčí při určování obvodu šatů.

Obvod kruhu potřebujete znát také při řemeslných pracích, při stavění ohrádky kolem vířivky nebo jen při řešení matematické úlohy do školy.

Jak zjistit obvod kruhu?

Jak jsme již uvedli, obvod neboli kružnice je vzdálenost kolem kruhu nebo jakéhokoli kruhového útvaru. Obvod kruhu je stejný jako délka přímky, která je přeložena nebo ohnuta tak, aby vznikl kruh. Obvod kruhu se měří v metrech, kilometrech, yardech, palcích atd.

Existují dva způsoby, jak zjistit obvod kruhu. První vzorec zahrnuje použití poloměru a druhý použití průměru kruhu. Je důležité si uvědomit, že oba dva způsoby dávají stejný výsledek.

Podívejme se na to.

Obvod kruhu je dán vztahem;

C = 2 * π* R = 2πR

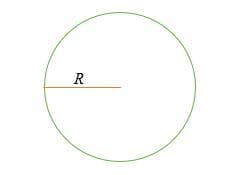
kde,

C = obvod neboli perimetr,

R = poloměr kruhu,

π = matematická konstanta známá jako pí

nebo

C = π* D = π D

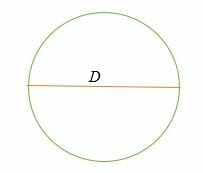
kde, D = 2R = průměr kruhu

Pro každý kruh je poměr jeho obvodu a průměru roven konstantě známé jako pí.

Obvod/průměr = pí

C /D = pí neboli C/2R = pí

Přibližná hodnota pí (π) = 22/7 = 3,1415926535897….. (nekoncová hodnota)

Pro snadnější výpočet obvodu kruhu se bere hodnota pí 3,14 (π = 3,14).

Podívejme se na několik příkladů níže, abychom si oprášili pojem obvodu.

Příklad 1

Najděte obvod kruhu o poloměru 8 cm.

Řešení

Obvod = 2 * π* R = 2πR

= 2 * 3,14 * 8

= 50,24 cm.

Příklad 2

Vypočítejte obvod kruhu, jehož průměr je 70 mm

Řešení

Obvod = π* D = π D

= 3,14 * 70

= 219. Jaký je obvod kruhu?8 mm

Příklad 3

Vypočítejte obvod kruhové květinové zahrady, jejíž poloměr je 10 metrů.

Řešení

Obvod = 2 * π* R = 2πR

= 2 * 3,14 * 10

= 62,8 m.

Příklad 4

Obvod kruhu je 440 yardů. Zjistěte průměr a poloměr kružnice.

Řešení

Obvod = 2 * π* R = 2πR

440 =2 * 3,14 * R

440 = 6. Jaký je průměr kružnice?28R

Obě strany vydělíme 6,28 a dostaneme,

R = 70,06

Poloměr kruhu je tedy 70,06 yardů. Ale protože průměr je dvojnásobek poloměru kruhu, pak je průměr roven 140,12 yardů.

Příklad 5

Průměr kol jízdního kola je 100 cm. Kolik otáček udělá každé kolo, aby ujelo vzdálenost 157 metrů

Řešení

Vypočítej obvod kola jízdního kola.

Obvod = π D

= 3. Jaký je obvod kola jízdního kola?14 * 100

= 314 cm

Chceme-li získat počet otáček kola, vydělíme ujetou vzdálenost obvodem kola.

Před dělením musíme 157 metrů převést na cm, takže 157 vynásobíme 100 a dostaneme 15700 cm. Proto,

Počet otáček = 15700 cm/314 cm

= 50 otáček.

Příklad 6

Kus drátu ve tvaru obdélníku o délce 100 cm a šířce 50 cm je ustřižen a přeložen tak, aby vznikl kruh. Vypočítejte obvod a poloměr vzniklé kružnice.

Řešení

Obvod vzniklé kružnice = obvod obdélníkového drátu.

Obvod obdélníku = 2(D + Š)

= 2(100 + 50) cm

= 2 * 150 cm

= 300 cm.

Obvod kružnice bude tedy 300 cm.

Nyní vypočítáme její poloměr.

Obvod = 2 π R

300 cm = 2 * π * R

300 cm = 2 * 3,14 * R

300 cm = 6,28R

Obě strany vydělte číslem 6,28.

R=47.77 cm

Poloměr kružnice tedy bude 47,77 cm.

Příklad 7

Poloměr každého kola motocyklu je 0. 85 m. Jak daleko ujede motocykl, jestliže každé kolo udělá 1000 otáček. Předpokládejme, že se motocykl pohybuje po přímce.

Řešení

Nejprve zjistíme obvod kola.

Obvod = 2 π R

= 2 * 3,14 * 0,85

= 5,338 m.

Pro zjištění ujeté vzdálenosti vynásobíme obvod kola počtem provedených otáček.

Vzdálenost = 5,338 * 1000

= 5338 m

Ujetá vzdálenost je tedy rovna 5,338 km.

Pracovní otázky

1. Mikovi a jeho přátelům se podává 12palcová pizza. Mike má zájem vypočítat její obvod. Pomoz mu!
2. Obvod určitého čtverce je 1/3 plochy určitého kruhu. Je-li délka čtverce L jednotek, určete průměr kružnice ve vztahu k L.

Odpovědi

1. 12π palců nebo 37,67 palce
2. 12L/π jednotek

Předchozí lekce | Hlavní strana | Další lekce

.