Funkce nebo mapování

Nyní se budeme v rámci funkce nebo mapování zabývat zvláštním druhem vztahů, které se nazývají funkce nebo mapování. Abychom je pochopili, uvedeme si několik příkladů z reálného života.

Všechny tyto otázky mají
jednotlivé odpovědi. Podívejme se, jak
to můžeme vztáhnout
k mapování výuky.

● Odkud vychází slunce?“

Východ

● Které je hlavní město Indie?

Dillí

● Jaký je nástupce čísla 4?

5

● Jaký je součet čísel 5 a 3?

8

Mapování nebo funkce:

Jsou-li A a B dvě neprázdné množiny, pak se říká, že relace ‚f‘ z množiny A do množiny B je funkce nebo mapování,
● jestliže každému prvku množiny A je přiřazen jedinečný prvek množiny B.

● Funkci ‚f‘ z A do B označujeme f : A → B.

● Je-li f funkce z A do B a x ∈ A, pak f(x) ∈ B, kde f(x) se nazývá obraz x pod f a x se nazývá předobraz f(x) pod ‚f‘.

Poznámka:

Aby f bylo zobrazením z A do B:

● Každý prvek A musí mít obraz v B. Přilehlý obrázek nepředstavuje zobrazení, protože prvek d v množině A není spojen s žádným prvkem množiny B.

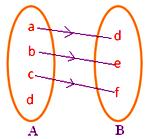
● Žádný prvek A nesmí mít více než jeden obraz. Sousední obrázek nepředstavuje zobrazení, protože prvku b množiny A jsou přiřazeny dva prvky d, f množiny B.

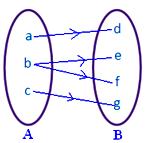
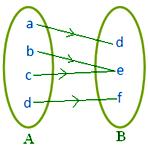
● Různé prvky A mohou mít v B stejný obraz. Přilehlý obrázek představuje zobrazení.

Poznámka:

Každé zobrazení je relace, ale každá relace nemusí být zobrazení.

Funkce jako zvláštní druh relace:

Připomeňme si a zopakujme si funkci jako zvláštní druh relace Předpokládejme, že A a B jsou dvě neprázdné množiny, pak pravidlo „f“, které spojuje každý prvek A s jedinečným prvkem B, se nazývá funkce neboli mapování z A na B.
Jestliže ‚f‘ je mapování z A na B,

vyjádříme to jako f: A → B

čteme to jako ‚f‘ je funkce z A na B.
Jestliže ‚f ‚ je funkce z A na B a x∈A a y∈B, pak říkáme, že y je obrazem prvku x pod funkcí ‚ f ‚ a označujeme ho f(x).
Zapíšeme ji tedy jako y = f(x)

Zde se prvek x nazývá předobraz y.

Pro funkci z A do B.
● A a B by měly být neprázdné.

● Každý prvek A by měl mít obraz v B.

● Žádný prvek ‚A‘ by neměl mít více než jeden obraz v ‚B‘.
Poznámka:

● Dva nebo více prvků A mohou mít stejný obraz v B.

● f : x → y znamená, že při funkci ‚f‘ z A do B má prvek x A obraz y v B.

● Je nutné, aby každý obraz f byl v B, ale v B mohou být některé prvky, které nejsou obrazy f žádného prvku A.

● Vztahy a zobrazení

Uspořádaná dvojice

Kartézský součin dvou množin

Vztah

Oblast a rozsah vztahu

Funkce nebo zobrazení

Oblast ko-.doména a rozsah funkce

● Vztahy a mapování -. Pracovní listy

Pracovní list k matematickému vztahu

Pracovní list k funkci nebo mapování

.

Úlohy z matematiky pro 7. třídu

Cvičení z matematiky pro 8. třídu
Z funkcí nebo mapování na HLAVNÍ STRÁNKU